惯性矩与惯性积的重要性及应用

图5-3与图5-1一样，代表任意截面的平面图形。在图形内任取一微面积dA，其坐标分别为y和z。将乘积y2dA和z2dA分别称为微面积dA对z轴和y轴的惯性矩，而将积分和分别定义为截面对z轴和y轴的惯性矩，也称截面二次矩（积分沿整个截面面积进行），用Iz和Iy代表截面对z轴和y轴的惯性矩，则有

在讨论扭转时曾遇到极惯性矩Ip，图5-3中截面对坐标原点O的极惯性矩由下面积分来定义

式中，ρ是微面积到坐标原点O的距离。

截面对轴的惯性矩与对坐标原点的极惯性矩之间存在着一定的关系。在图5-3中有

将此式代入式（5-7），得

即

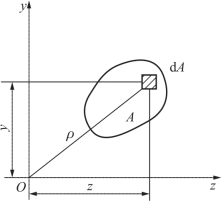
图5-3　任意截面的平面图形

上式就是Ip与Iy、Iz间的关系，它表明：截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。

微面积与其坐标y，z的乘积yzdA称为微面积dA对z、y二轴的惯性积，而把积分定义为截面对z、y二轴的惯性积，并以Izy表示，即

惯性矩Iz、Iy和惯性积Izy都是对轴来说的，同一截面对不同轴的数值不同。极惯性矩是对点（称极点）来说的，同一截面对不同点的极惯性矩值也各不相同。从式（5-6）、式（5-7）、式（5-9）之定义可知，惯性矩永为正值，而惯性积则为代数量。惯性矩和惯性积的常用单位为m4。

惯性矩、惯性积及上节讨论的静矩等均属平面图形的纯几何性质，其本身是没有物理意义的。

【例5-2】　图5-4（a）为一矩形截面，z、y轴均通过形心，且z轴平行于底边，y轴平行于侧边。试计算该矩形截面对z轴和y轴的惯性矩及对z、y二轴的惯性积。

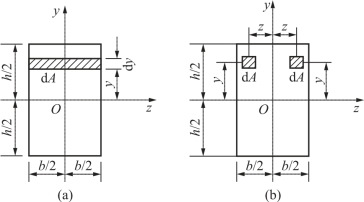
图5-4　例5-2图(www.xing528.com)

解：先计算对z轴的惯性矩。取平行于z轴的阴影面积[图5-4（a）]为微面积，则

用同样办法可求得对y轴的惯性矩为

下面讨论惯性积。y轴为截面的对称轴，在y轴两侧对称位置取相同的微面积dA[图5-4（b）]，由于处在对称位置的zydA值大小相等，符号相反（y坐标相同，z坐标差一符号），因此该二微面积对z、y轴的惯性积之和等于零。将此推广到整个截面，则有

这说明：只要z、y轴之一为截面的对称轴，则截面对该二轴的惯性积一定等于零。

【例5-3】　图5-5为一箱形截面，z轴过形心且平行于底边，试求截面对z轴的惯性矩。

解：，在此题中A为箱形截面面积，此截面面积相当于整个矩形面积A总（b·h）减去中间部分的面积A1（b1·h1）。根据惯性矩的定义及例5-2，箱形截面对z轴的惯性矩为

图5-5　例5-3图

【例5-4】　图5-6为直径为d的圆形截面，z、y轴通过圆心。试求圆截面对圆心O的极惯性矩和对z轴的惯性矩。

图5-6　例5-4图

解：取图示的环形面积为微面积，即

由于z、y轴通过圆心，所以Iz＝Iy，由式（5-8）可得

所以