静矩和形心的计算方法

图5-1所示的平面图形代表一任意截面，在图形平面内选取一对直角坐标轴如图所示。在图形内任取一微面积dA，其坐标分别为y和z。我们把乘积ydA和zdA分别称为微面积dA对z轴和y轴的静矩，而把积分和分别定义为该截面对z轴和y轴的静矩（积分是沿整个截面面积进行）。如果用Sz和Sy分别代表截面对z轴和y轴的静矩，则有

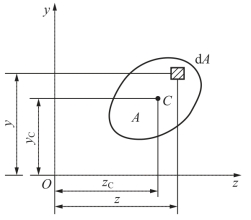
图5-1　任意一截面

静矩是对一定的轴而言的，同一截面对不同轴的静矩值不同。从式（5-1）的定义可知，静矩值可正、可负，也可为零。其单位为m3。

若截面形心的坐标为zC、yC（C为截面形心），将面积视为平行力，即看成等厚、均质薄板的重力，根据合力矩定理可得

或

当截面形心的位置已知时，可用式（5-2）来计算静矩。如果截面面积和静矩已知时，可由该式来确定形心位置，即

(www.xing528.com)

如果z轴和y轴通过截面形心，则用yC、zC都等于零。由式（5-2）可知，此时Sz＝0，Sy＝0。即截面对通过其形心的轴的静矩等于零（反之，若截面对某轴的静矩等于零，则该轴也一定通过截面形心）。

有些截面是由几个简单图形组成的，这类截面称为组合截面。在计算组合截面对某轴的静矩时，可分别计算各简单图形对该轴的静矩，然后再代数相加，即

式中Ai和yi、zi分别代表各简单图形的面积和形心坐标，n为简单图形的个数。将该式代入式（5-3），可得计算组合截面形心坐标的公式，即

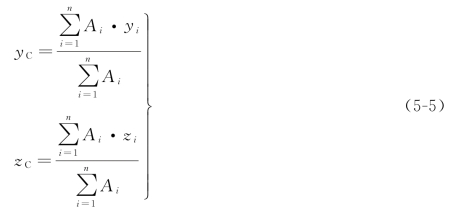
【例5-1】　图5-2为对称的T形截面，其尺寸如图所示。试求该截面的形心位置。

解：因图形相对y轴对称，其形心一定在该对称轴上。取一对直角参考坐标轴y、z，其中y为截面的对称轴，因而zC＝0，只需计算yC值。将截面分成I、Ⅱ两个矩形，则

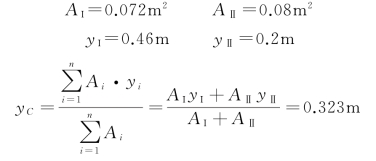
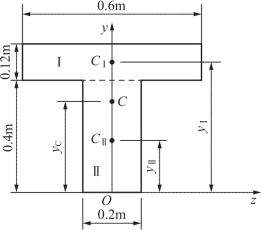
图5-2　例5-1图