弯矩、剪力与荷载集度的关系分析

这里将要讨论两种内力——剪力FS（x）和弯矩M（x）之间及它们与梁上分布荷载q（x）之间的关系。由于内力是由梁上的荷载引起的，而弯矩、剪力及分布荷载的集度又都是x的函数，因此，它们三者之间一定存在着某种联系。如能找到反映弯矩、剪力和荷载集度三者联系的关系式，将有利于内力的计算和内力图的绘制与校核。

下面推导三者间的关系。设在如图4-29（a）所示梁上作用有任意的分布荷载q（x），q（x）以向上为正，向下为负。我们取梁中的微段来研究。在距左端为x处，截取长度为dx的微段梁[图4-29（b）]。设该微段梁左侧横截面上的剪力和弯矩分别为FS（x）和M（x），微段梁右侧横截面上的剪力和弯矩分别为FS（x）＋dFS（x）和M（x）＋dM（x）。此微段梁除两侧存在剪力、弯矩外，在上面还作用有分布荷载q（x）。由于dx很微小，可不考虑q（x）沿dx的变化而看成均布的。

图4-29　弯矩、剪力和荷载集度

因为梁是处于平衡状态，所以截取的微段梁也应该是平衡的。由微段梁的平衡条件∑Fy＝0，得

经整理得

即剪力对x的导数等于梁上相应位置分布荷载的集度。(www.xing528.com)

由微段梁的平衡条件∑MO＝0（矩心O取在右侧截面的形心）得

略去二次微量经整理得

即弯矩对x的导数等于相应截面上的剪力。

从式（4-2）和式（4-3）又可得

式（4-2）、式（4-3）、式（4-4）就是弯矩、剪力、荷载集度间普遍存在的关系式。

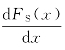一阶导数的几何意义是代表曲线上的切线斜率，所以与分别代表剪力图与弯矩图上的切线斜率。＝q（x）表明：剪力图中曲线上各点的切线斜率等于梁上各相应位置分布荷载的集度。＝FS（x）表明：弯矩图中曲线上各点的切线斜率等于各相应截面上的剪力。此外，由数学上知道，二阶导数的正、负可用来判定曲线的凹向。