梁的内力及求解方法

与承受拉伸、压缩的构件一样，梁在弯曲时其横截面也要产生内力。内力的大小与梁的强度和刚度有关，只有在分析和计算内力的基础上，才能进一步进行梁的强度和刚度计算。

下面讨论梁在外力作用下，横截面上将产生哪些内力以及这些内力如何计算。

图4-16（a）为一简支梁，其上作用有荷载，此梁在荷载及支座反力共同作用下处于平衡状态。现讨论距左支座为a处的横截面m－m上的内力。

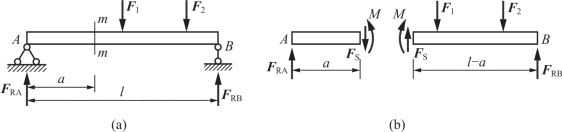
图4-16　简支梁

研究内力仍采用截面法。在梁的截面m－m处，用一假想的垂直于梁轴线的平面将梁截为两段，这里研究左段脱离体。因为梁原是一整体，截开后的每段梁仍保持与没有截开前的受力情况完全一样，所以，左段梁上除作用有反力FRA外，在截开的截面上还有右段梁对左段梁的作用力，此力就是梁的内力。此内力的形式可从平衡方面来分析。梁原来是平衡的，截开后的每段梁也应该是平衡的。左段梁上作用有向上的力FRA，根据∑Fy＝0可知，在m－m截面上应该有向下的力FS与FRA相平衡。力FRA对m－m截面的形心O又存在着顺时针转的力矩FRAa，根据∑Mo＝0，则在m－m截面上还必定有一逆时针转的力偶矩M与FRAa相平衡。力FS和力偶矩M就是横截面上产生的两种不同形式的内力，FS称为剪力，力偶矩M称为弯矩。

剪力的常用单位为N或kN，弯矩的单位为N·m或kN·m。m－m截面上的剪力和弯矩的具体值可由左段梁的平衡条件来求得，即

∑Mo＝0，M－FRAa＝0，M＝FRAa（矩心O是m－m截面的形心）。

m－m截面上的内力值也可通过右段梁的平衡来求得，其结果与通过左段梁求得的完全相同，但方向与左段梁上的相反。

综上所述，梁在外力作用下，横截面上产生两种形式的内力——剪力和弯矩，求内力的基本方法仍是截面法。用截面法求内力的步骤是：在欲求内力的截面处把梁截开（暴露出内力），任取一脱离体并画出脱离体的受力图，再依脱离体的平衡条件求出各内力值。在取脱离体时，取左、右段均可，应以计算简便为准。

截面上的内力是有方向的，为了区分，对内力符号做如下规定：

（1）剪力符号。当截面上的剪力使考虑的脱离体有顺时针方向转动趋势时为正[图4-17（a）]，反之为负[图4-17（b）]。按此规定，如考虑左段脱离体时，FS向下为正，向上为负；如考虑右段脱离体时，则FS向上为正，向下为负。

（2）弯矩符号。当截面上的弯矩使考虑的脱离体凹向上弯曲（即下边受拉，上边受压，图4-18（a）时为正，凹向下弯曲（即上边受拉、下边受压，图4-18（b）时为负。

图4-17　剪力符号

图4-18　弯矩符号

按上述规定，不论考虑左段脱离体还是考虑右段脱离体，同一截面上内力的符号总是一致的。

按此规定，图4-16（b）所示的m－m截面上的剪力和剪矩均为正值。

【例4-3】　一外伸梁，尺寸及梁上荷载如图4-19（a）所示，试求截面1-1、2-2上的剪力和弯矩。

解：首先求出支座反力。考虑梁的整体平衡

得

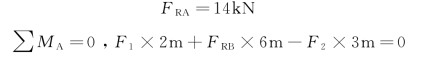
得

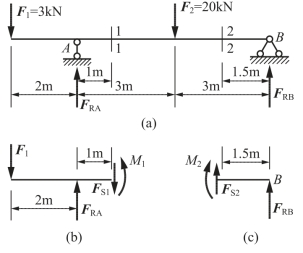
图4-19　例4-3图

（1）求截面1-1上的内力

在截面1-1处将梁截开，取左段脱离体并在脱离体上标明未知内力FS1和M1，内力的方向均按符号规定的正号方向标出[图4-19（b）]。考虑脱离体平衡

得

得

求得的FS1和M1均为正值，表示截面1-1上内力的实际方向与假定的方向相同。按内力的符号规定，它们都是正值。

（2）求截面2－2上的内力

在2－2处将梁截开并取右段脱离体（右段梁上外力少，计算简便），内力FS2、M2的方向仍按正号方向标出，考虑脱离体平衡。

得(www.xing528.com)

得

这里求得的FS2为负值，表明FS2的实际方向与假定的方向相反，FS2的方向应向下。它使所在的脱离体有逆时针转趋势，按剪力符号规则，FS2为负剪力。

【例4-4】　一悬臂梁，其尺寸及梁上荷载如图4-20（a）所示。试求截面1－1上的剪力和弯矩。

解：此题不需求固定支座处的反力，可取右段脱离体。右段的受力图如图4-20（b）所示，列平衡方程时，分布荷载可用合力来代替。

图4-20　例4-4图

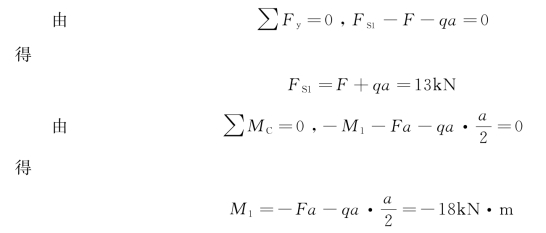
求得的M1为负值，表明M1的实际方向与假定的方向相反。按弯矩的符号规定，M1也是负的。此题取左段脱离体时，应先求出固定支座处的反力。

从以上用截面法求内力的过程看到：梁的任一横截面上的内力是考虑脱离体平衡，剪力FS是由平衡条件∑Fy＝0求得的；弯矩M是由平衡条件∑M＝0求得的，参照例4-3、例4-4可得出下列结论。

（1）梁的任一横截面上的剪力在数值上等于该截面一侧（左侧或右侧）所有的竖向外力（包括斜向外力的竖向分力）的代数和。

（2）梁的任一横截面上的弯矩在数值上等于该截面一侧（左侧或右侧）所有的外力（包括外力偶）对该截面形心的力矩的代数和。

利用上述结论来计算某指定截面上的内力非常简便，此时不需画脱离体的受力图和列平衡方程，只要梁上的外力已知，任一横截面上的内力值均可根据梁上的外力逐项直接写出。下面举例说明。

【例4-5】　一简支梁，尺寸及梁上荷载如图4-21（a）所示，试求截面1－1上的剪力和弯矩。

解：先求出支座反力。由梁的整体平衡求得

图4-21　例4-5图

截面1－1上的剪力等于该截面左侧（或右侧）所有竖向外力的代数和，即等于FRA与F1的代数和（若考虑右侧，则为F2与FRB的代数和）。FRA、F1每项的正负，可根据剪力的符号规则逐项定出。FRA是向上的，它引起截面1－1上的剪力向下，该剪力使左段梁有顺时针转趋势，所以FRA项是正的。F1是向下的，它引起截面1－1上的剪力是负的。所以截面1－1上的剪力值为

截面1－1上的弯矩等于该截面左侧（或右侧）所有外力对该截面形心的力矩的代数和，即等于FRA×3与F1×2的代数和（若考虑右侧，则为F2×1与FRB×3的代数和）。每项的正负，根据弯矩的符号规则（即根据梁的凹向）逐项定出。为了便于确定每项外力引起的截面1－1上弯矩的正负，即便于看清梁的凹向，可将左段看成截面1－1处为固定支座的悬臂梁[图4-21（b）、（c）]。显然，FRA使梁凹向上弯曲，所以FRA×3项是正的；F1使梁凹向下弯曲，F1×2项是负的。截面1－1上的弯矩则为

【例4-6】　试求图4-22（a）所示梁截面1－1和2－2上的剪力和弯矩。

解：首先求出支座反力。考虑梁的整体平衡，由∑MB＝0和∑Fy＝0求得

（1）截面1－1上的内力

截面1－1上的剪力等于该截面左侧的竖向力与的代数和，第一项为正，第二项为负，即

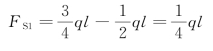
图4-22　例4-6图

截面1-1上的弯矩等于该截面左侧的所有外力（包括FRA、Me1和分布荷载的合力q·）对该截面形心的力矩的代数和，即等于三项的代数和。其中，第一项为正，其余两项为负（仍将左段梁看成截面1－1处为固定支座的悬臂梁，如图4-22（b）所示，所以截面1－1上的弯矩为

（2）截面2－2上的内力

求截面2－2上的内力时，应考虑右侧（右侧外力少，计算简便）。截面2－2右侧的竖向外力只有向上的FRB，故截面2－2的剪力为

截面2-2上的弯矩等于该截面右侧的外力Me2和FRB对截面2－2形心的力矩的代数和。FRB对截面2－2的力矩等于零，所以有

将截面2－2与Me2间的距离放大，并视为截面2－2处为固定支座的悬臂梁，此时梁的变形如图4-22（c）所示，故Me2引起的截面2－2的弯矩为负值。

由以上例题看出，用上述两结论计算任一横截面的内力时，由于省略了取脱离体及列平衡方程式的过程，因而非常简便，又称为简便法。但应指出，截面法是求内力的基本方法，应该在掌握截面法的基础上，再掌握该简便方法。建议读者，就例4-5、例4-6考虑右侧用简便法写出1－1截面的剪力和弯矩。