梁支座以及反力设计原则

支座（约束）反力的形式与梁的支座形式有关，常见的支座形式有下列三种。

1.固定铰支座

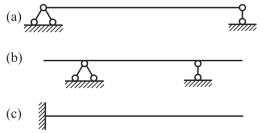
其简图如图4-9（a）所示。梁端在支座处可以转动，但不能移动。其反力通过铰的中心，方向可为任意的，通常将反力分解为水平反力FRx及竖向反力FRy，即该支座存在两个未知反力。

2.可动铰支座

图4-9　常见的支座形式

其简图如图4-9（b）所示。梁端在支座处可以转动和水平移动，但不能沿竖直方向移动，其只存在竖直方向的未知反力。

3.固定支座

其简图如图4-9（c）所示。梁端在支座处既不能转动，又不能沿任意方向移动，其未知反力一般为三个，即力FRx、FRy，和力矩M。

上述三类支座是理想的典型的情况，在实际工程中特别是在建筑工程中，梁的支座并不与之完全相同。当我们确定梁的支座属于哪种形式时，必须根据支座的具体情况加以分析。一般地说，当梁端被嵌固得很牢时，可视为固定支座；如果梁在支座处有可能发生微小转动时，便看成固定铰支座或可动铰支座。例如，厂房中的钢筋混凝土柱（图4-10），其插入基础部分较深，而且用混凝土与基础浇筑在一起，柱下部被嵌固得很牢，不能发生转动与移动，此柱下端即为固定支座。又如，本章第一节中图4-1所示的楼板梁，虽然梁嵌入墙内，但因嵌入长度a（图4-11）很小，其嵌固作用很弱，当砖墙稍有松动时，梁端便可能发生微小转动，所以此处应看成固定铰支座而不能认为是固定支座。

图4-10　厂房中的钢筋混凝土柱

图4-11　梁嵌入墙内

将梁的实际支承简化为上述理想支座，在力学上属于确定计算简图问题。在工程中，将一受力构件（或结构）抽象为力学上的计算简图，是一项重要而又复杂的工作，其遵循的基本原则应该是：按计算简图计算的结果应符合客观实际；同时，应尽可能使计算简单、方便。

工程中常用的简单梁依支座情况划分为下列几种：

（1）简支梁。一端为固定铰支座，另一端为可动铰支座的梁[图4-12（a）]。

（2）外伸梁。一端或两端向外伸出的简支梁[图4-12（b）]。

（3）悬臂梁。一端为固定支座，另一端自由的梁[图4-12（c）]。

以上三种形式的梁的未知的支座反力都是三个。我们讨论的是梁的平面弯曲，梁上的荷载和梁的支座反力都在同一平面内，通过平面力系的三个平衡方程，便可求出各未知反力。

用平衡方程可求出未知反力的这类梁称为静定梁。如果仅用平衡方程不能求出梁的全部未知力，这类梁则称为超静定梁，又称静不定梁。例如，在简支梁中间再加一可动铰支座[图4-13（a）]就成为超静定梁。图4-13（b）所示的梁也是超静定梁。本章只讨论静定梁。

(www.xing528.com)

图4-12　简单梁依支座情况划分

图4-13　超静定梁

【例4-1】　简支梁受力如图4-14（a）所示，试求该梁的支座反力。

解：因梁上无水平荷载，故A处水平反力等于零，A、D处竖向反力FRA、FRD的方向均假定向上。求FRA和FRD时，将分布荷载用合力来代替，合力位于CD之中点处，其值为4q[图4-14（b）]。

图4-14　例4-1图

考虑梁的平衡

经校核反力FRA、FRD无误。

【例4-2】　承受三角形分布荷载的简支梁如图4-15所示，试求该梁的支座反力。

解：求反力时，将三角形分布荷载用合力来代替，合力值为（即三角形的面积），合力的位置如图中所示。

考虑梁的平衡

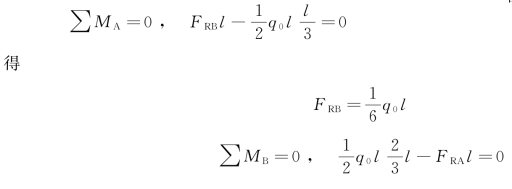
图4-15　例4-2图

得

校核：

经校核反力FRA、FRB无误。