闭口薄壁截面杆的计算方法与应用

工程中有一类薄壁截面的壁厚中线是一条封闭的折线或曲线，这类截面称为闭口薄壁截面，如环形薄壁截面和箱形薄壁截面。桥梁中经常采用箱形截面梁，它在外力作用下也可能出现扭转变形。本节只讨论这类杆件在自由扭转时的应力和变形计算。

设有一横截面为任意形状、变厚度的闭口薄壁截面等直杆，两自由端承受一对扭转外力偶作用，如图3-26（a）所示。由于杆横截面上的内力为扭矩，因此，其横截面上将只有切应力。又因是闭口薄壁截面，故可假设切应力沿壁厚无变化，且其方向与壁厚的中线相切，如图3-26（b）所示。当杆的壁厚远小于其横截面尺寸时，由假设所引起的误差在工程计算中是允许的。

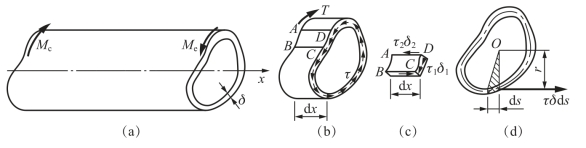
图3-26　闭口薄壁杆件受扭及其横截面上的切应力

取长为dx的杆段，用两个与壁厚中线正交的纵截面从杆壁中取出小块ABCD，如图3-26（c）所示。设横截面上C和D两点处的切应力分别为τ1和τ2，而壁厚则分别为δ1和δ2。根据切应力互等定理，其上、下两纵截面上应分别有切应力τ2和τ1，由平衡方程

可得

由于所取的两纵截面是任意选择的，故上式表明，横截面沿其周边任一点处的切应力τ与该点处的壁厚δ之乘积为一常数，即

为找出横截面上的切应力τ与扭矩T之间的关系，沿壁厚中线取出长为ds的一段，在该段上的内力元素为τδds，如图3-26（d）所示，其方向与壁厚中线相切。其对横截面平面内任一点O的矩为

式中，r是从矩心O到内力元素τδds作用线的垂直距离。由力矩合成原理可知，截面上的扭矩应为dT沿壁厚中线全长s的积分。注意到式（3-41），即得

由图3-26（d）可知，rds为图中阴影线三角形面积的2倍，故其沿壁厚中线全长s的积分应是该中线所围面积A0的2倍。于是，可得

或

上式即闭合薄壁截面等直杆在自由扭转时横截面上任一点处切应力的计算公式。式（3-42）的形式与式（3-1）相同，但在应用上则具有普遍性。

由式（3-41）可知，壁厚δ最薄处横截面上的切应力τ为最大。于是，由式（3-42）可得杆横截面上的最大切应力为

式中，δmin为薄壁截面的最小壁厚。

闭口薄壁截面等直杆的单位长度扭转角φ′可按功能原理来求解。

由纯剪切应力状态下的应变能密度vε的表达式，可得杆内任一点处的应变能密度为

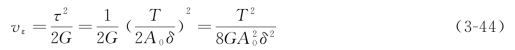
又根据应变能密度vε计算扭转时杆内的应变能，可得单位长度杆内的应变能为

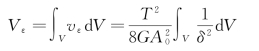(www.xing528.com)

式中，V为单位长度杆壁的体积，dV＝1·δ·ds＝δds。将dV代入上式，并沿壁厚中线的全长s积分，得

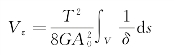
然后，计算单位长度杆两端截面上的扭矩对杆段的相对扭转角φ′所做的功。由于杆在线弹性范围内工作，因此，所做的功W＝Tφ′。由功能原理可知，Vε和W在数值上相等，从而解得

即得所要求的单位长度扭转角。式中的积分取决于杆的壁厚δ沿壁厚中线s的变化规律。当壁厚δ为常数时，则得

式中，s为壁厚中线的全长。

【例3-10】　横截面面积A、壁厚δ、长度l和材料的切变模量均相同，而截面形状不同的三根闭口薄壁杆，分别如图3-27（a）、（b）和（c）所示。若分别在杆的两端承受相同的扭转外力偶矩Me，试求三杆横截面上的切应力之比和单位长度扭转角之比。

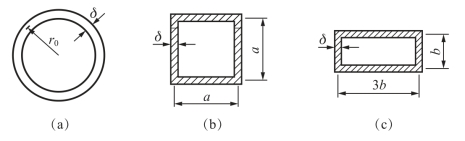
图3-27　例3-10图

解：（1）对于薄壁圆截面[图3-27（a）]，由于

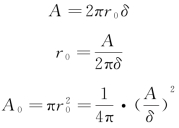
可得τa＝

对于薄壁正方形截面，如图3-27（b）所示，由于

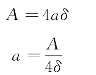
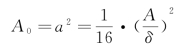
可得τb＝

对于薄壁矩形截面，如图3-27（c）所示：由于

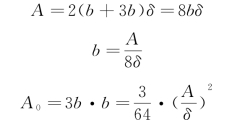
可得τc＝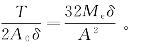

可见，三杆截面的扭转切应力之比为

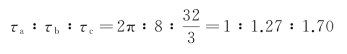
（2）由于三杆的单位长度扭转角分别为

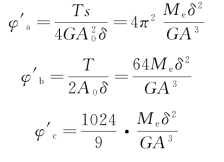
故三杆扭转角之比为

上述计算结果表明，对于相同截面面积的同一材料而言，无论是强度或是刚度，都是薄壁圆截面最佳，薄壁矩形截面最差。这是因为薄壁圆截面壁厚中线所围的面积A0最大，而薄壁箱形截面在其内角处还将引起应力集中。