开口薄壁截面杆的应用及特点

在土建工程中，常采用一些薄壁截面的构件。若薄壁截面的壁厚中线是一条不封闭的折线或曲线，这种截面称为开口薄壁截面，如各种轧制型钢（工字钢、槽钢、角钢等）或I形、槽形、T形截面（图3-24）等。在外力作用下，这类截面的杆件常会发生扭转变形，本节只讨论在自由扭转时应力和变形的近似计算。

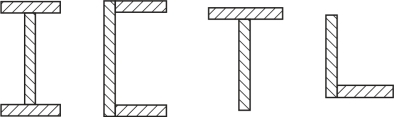
图3-24　几种薄壁杆件截面的形状

对于某些开口薄壁截面杆，例如各种轧制型钢，其横截面可以看作由若干狭长矩形所组成的组合截面（图3-24）。根据杆在自由扭转时横截面的变形情况，可做出如下假设：杆扭转后，横截面周线虽然在杆表面上变成曲线，但在其变形前平面上的投影形状仍保持不变。当开口薄壁杆沿杆长每隔一定距离有加劲板时，上述假设基本上与实际变形情况相符。由假设得知，在杆扭转后，组合截面的各组成部分所转动的单位长度扭转角与整个截面的单位长度扭转角φ′相同，于是，有以下变形相容条件：

式中，φ′i（i＝1，2，…，n）代表组合截面中组成部分i的单位长度扭转角。由式（3-31）和式（3-32），可得补充方程

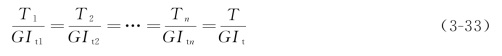
式中，Iti＝hδ3（i＝1，2，…，n），Ti为组合截面中组成部分i上分担的扭矩，而It和T则分别代表整个组合截面的相当极惯性矩和扭矩。由合力矩和分力矩的静力关系，可得

联立式（3-33）和式（3-34），消去T、G后，即得整个截面的相当极惯性矩为

对于开口薄壁截面，当其每一组成部分i的狭长矩形厚度δi与宽度hi之比很小时，可将式（3-35）改写为

为了求得整个截面上的最大切应力τmax，需先研究其每一组成部分i上的最大切应力τmax。利用狭长矩形截面中Wti＝和式（3-33）的关系，矩形截面杆在扭转时的最大切应力为

由式（3-37）可见，该组合截面上的最大切应力将发生在厚度为δmax的组成部分的长边处，其值为

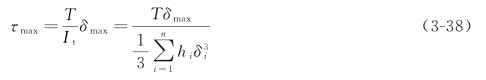
式中，δmax为组合截面所有组成部分中厚度的最大值。(www.xing528.com)

在计算由型钢制成的等直杆的扭转变形时，由于实际型钢截面的翼缘部分是变厚度的，且在连接处有过渡圆角，这就增加了杆的刚度，故应对It的表达式做如下修正，并将修正后的It改写为I′t：

式中，η为修正因数。对于角钢截面、槽钢截面、T形钢截面和工字钢截面，η分别取1.00、1.12、1.15和1.20。在计算单位长度扭转角时，仍采用式（3-30）的第二式，并以I′t代替式中的It。

【例3-9】　如图3-25所示，一长度为l、厚度为δ的薄钢板卷成平均直径为D的圆筒，材料的切变模量为G，其两端承受扭转外力偶矩Me，试求：

（1）在板边为自由的情况下，如图3-25（a）所示，薄壁筒横截面上的切应力分布规律，以及其最大切应力和最大相对扭转角；

（2）当板边焊接后，如图3-25（b）所示，薄壁筒横截面上的切应力分布规律，以及其最大切应力和最大相对扭转角。

图3-25　例3-9图

解：（1）开口薄壁圆筒的应力和变形

在板边为自由的情况下，可将开口环形截面展直，视为狭长矩形截面。其横截面上的切应力沿壁厚呈线性变化，如图3-25（a）所示。最大切应力发生在开口薄壁圆筒的内、外周边处。对于薄壁杆，（即）大于10，由表3-1得α≈β≈于是，最大切应力和最大相对扭转角分别为

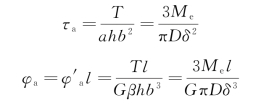
（2）闭口薄壁圆筒的应力和变形

当板边焊接后，则成闭口薄壁圆筒，其横截面上的切应力沿壁厚为均匀分布，如图3-25（b）所示。切应力和最大相对扭转角分别为

开口薄壁圆筒与闭口薄壁圆筒相比较：

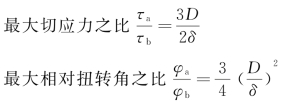
若D＝20δ，则τa＝30τb，φa＝300φb。可见，开口薄壁圆筒的最大切应力和最大相对扭转角均远大于闭口薄壁圆筒。