探究矩形截面杆的扭转机理

如图3-22（a）所示，对于矩形截面杆的扭转问题，根据切应力互等定理可以得出，横截面上切应力的分布具有下述特点。

（1）截面周边各点处的切应力方向一定与周边平行（或相切）。设截面周边上某点A处的切应力为τA，如其方向与周边不平行，则必有与周边垂直的分量τn，因τ′n＝0，故τn＝0，所以截面周边的切应力一定与周边平行。

（2）截面凸角（B点）处的切应力一定为零，其道理同上。

在图3-22（b）所示的矩形截面（设h＞b）上，画出了沿周边的切应力分布，最大切应力发生在长边中点。最大切应力τmax、单位长度扭转角φ′及短边中点的切应力τ1按下列公式计算：

图3-22　矩形截面杆受扭后截面上的切应力及其分布

式中，T为截面扭矩；G为材料的切变模量；It和Wt分别称为矩形截面的相当极惯性矩和扭转截面系数；α、β、ξ是与边长比h/b有关的系数，其值如表3-1所示。

表3-1　矩形截面扭转的有关系数α、β、ξ（用于矩形截面扭转）

由表3-1可知，当h/b＞10（即狭窄矩形）时，α＝β≈1/3，ξ＝0.74。现以δ表示狭长矩形短边的长度（图3-23），并将α＝β≈1/3代入式（3-30）的前两式，得狭长矩形截面的最大切应力τmax与单位长度扭转角φ′为(www.xing528.com)

如图3-23所示为沿狭长截面的长边与短边切应力的分布情况。狭长截面长边各点，除了靠近两端的很小部分，切应力与长边中点A处的最大切应力相等。

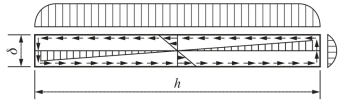
图3-23　狭窄矩形截面切应力分布

【例3-8】　两端自由的一矩形截面杆，高h＝90mm，宽b＝60mm，承受的扭矩T＝2500N·m，试计算杆的最大切应力τmax，如把截面做成圆形，使其面积相等，试比较两种情况下的τmax。

解：＝1.5。查表3-1，可得α＝0.231。由式（3-30）知，最大切应力为

矩形截面面积A＝60×90＝5400（mm2），相等的圆截面面积A＝＝5400mm2，故对应的圆截面直径D＝83mm，其扭转截面系数Wp＝＝112000mm3，对应的圆截面上的最大切应力为

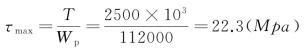
可见，在同样面积和承受相同扭矩的情况下，矩形截面所产生的最大切应力τmax要比圆形截面的大。