圆轴的塑性扭转分析

对于承受扭转的薄壁圆筒，当切应力达到剪切屈服极限τs时，意味着整个筒的材料过渡到塑性状态，已发生较大的塑性变形。而对于承受扭转的实心圆轴，当在周边的各点上出现塑性变形时，即τmax＝τs，整个截面上的塑性变形并不显著，因为不在边缘处的大部分材料还处于弹性状态。可把整个截面上的材料达到塑性状态作为圆轴的破坏状态或极限状态。现假设材料为线弹性-理想塑性材料，它的切应力τ和切应变γ的简化曲线，如图3-19所示。

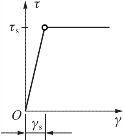
图3-19　线弹性-理想塑性材料的τ－γ关系

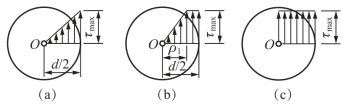
由式（3-10）可知，对于实心圆轴，可考虑仅圆轴的周边进入屈服状态，如图3-20（a）所示。

因轴尚处于弹性状态，轴的单位扭转角还可按式计算。若加大扭矩T，使轴截面处于弹塑性状态，即截面内部（ρ＜ρ1）保持弹性状态，外部（ρ＞ρ1）达到塑性状态，如图3-20（b）所示。在弹性部分，切应力τ＝Gρφ′；在外缘塑性部分，切应力τ＝τs；在弹性与塑性部分的交界处（ρ＝ρ1），切应力τs＝Gρ1φ′。

因此，弹性区域的半径为ρ1＝截面上的应力分布如图3-20（b）所示。

(www.xing528.com)

图3-20　受扭实心圆轴横截面上切应力的变化过程

应用静力平衡关系可求出截面上的扭矩T为

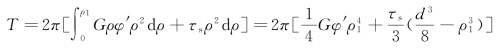
将τs＝Gρ1φ′代入上式，可得T＝

随着扭转角φ′的增加，弹性核心的半径无限地缩小，即ρ1→0，如图3-20（c）所示。此时扭矩T趋向极限值Tu，即该实心轴的极限扭矩。故有

根据极限扭矩可得出强度条件：

其中，n为安全因数。比较可知，对于理想塑性材料的同一圆轴，在静荷载作用下，其极限扭矩比按弹性设计承受的扭矩增大三分之一。