圆轴扭转的超静定问题简述

前面研究的轴，仅用平衡条件即可确定其约束力偶矩和扭矩，这类轴称为静定轴。而对于如图3-17所示的轴，其两端截面均固定，此时约束力偶矩增为两个，但有效平衡方程只有一个，不能确定它们的值，这类轴称为超静定轴，或静不定轴。这类问题统称为超静定问题。

未知力偶矩数减去有效平衡方程数等于超静定的次数，也等于多余约束数。显然，如图3-17所示的轴为一次超静定。与求解拉、压杆的超静定问题相似，除平衡方程外，还须借助协调条件和物理方程联合求解圆轴的超静定问题。

【例3-6】　如图3-17（a）所示，两端固定的实心圆杆AB，AC段直径为d1，长度为l1；BC段直径为d2，长度为l2。截面C处承受扭转外力偶矩Me。试求杆两端的约束力偶矩。

解：显然，杆两端约束力偶矩的转向应与外力偶矩Me的转向相反。为求两端的约束力偶矩，可将B端的约束解除，并加上力偶矩MB，如图3-17（b）所示。

为了使得解除B端约束后的静定系统与原来的超静定系统相当，须使其满足下列条件：φB＝0。在此条件下，可以认为求得的力偶矩MB与MA就是原超静定系统中的约束力偶矩。

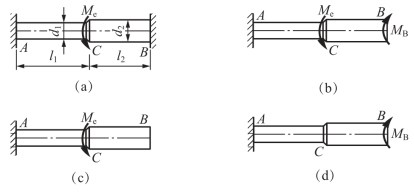
图3-17　例3-6图

在线弹性条件下，φB的大小满足叠加原理，即

其中，φB，Me为Me单独作用下引起的B端转角，φB，MB为MB单独作用下引起的B端转角。

由前面的讨论可知，

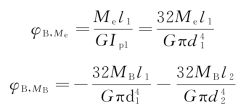
将以上两式代入式（a），并加以简化，可得(www.xing528.com)

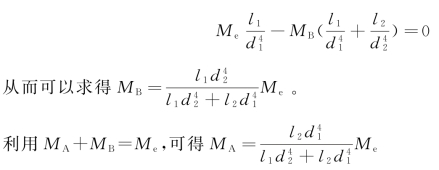
【例3-7】　如图3-18所示，一空心圆管A套在实心圆轴B的一端。管和轴在同一横截面处各有一直径相同的贯穿孔，两孔轴线之问的夹角为β。现在圆轴B上施加外力偶使圆轴B扭转。对准两孔，并穿过孔装上销钉。然后卸除施加在圆轴B上的外力偶。试问此时管和轴上的扭矩分别为多少？已知套管A和圆轴B的极惯性矩分别为IpA和IpB，管和轴的材料相同，切变模量为G。

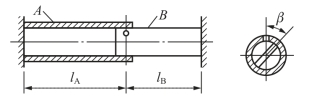
图3-18　例3-7图

解：安装套管A和圆轴B后，其连接处有一相互作用力偶矩T，在此力偶矩作用下，套管A转过一角度φA，圆轴B反方向转过的角度为φB，由套管A、圆轴B连接处的变形协调条件可知

由物理关系知

将式（b）、式（c）代入式（a），可得

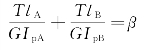
得

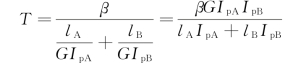
扭矩T是圆轴B对套管A的作用力，也是套管A对圆轴B的反作用力，所以套管A、圆轴B的扭矩相同，大小均为T。