圆轴扭转的应变能

当圆杆受到外力偶矩作用而发生扭转变形时，杆内将积蓄应变能。下面从纯剪切单元体的变形入手，推导扭转应变能的计算公式。

如图3-14所示是从构件取出的受纯剪切的单元体，假设单元体左侧面固定，右侧面上的剪力为τdydz，因有剪切变形，右侧面向下错动的距离为γdx。现给切应力一个增量dτ，相应切应变的增量则为dγ，右侧面向下的位移增量便为dγdx。因此剪力τdydz在位移dγdx上所做的功为τdydz·dγdx。其总功应为

根据功能原理，单元体内所积蓄的应变能dVε在数值上等于dW，故

式中，dV＝dxdydz为单元体的体积。因此，单位体积内的应变能（应变能密度）vε。为

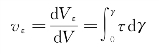
这表明，vε等于τ－γ曲线下的面积。当τ≤τp时，τ与γ呈线性关系，于是有

图3-14　纯剪切的单元体及切应力-切应变关系曲线

因τ＝Gγ，上式也可写成

求得杆件任一点处的应变能密度vε后，整个杆件的应变能Vε即可由积分进行计算：

式中，V为杆件的体积；A为杆件的面积；l为杆长。

当T、Ip为常数时，将τ＝及式（3-25）代入上式，可得杆内的应变能为

以上应变能表达式也可利用外力功与应变能数值上相等的关系，直接从作用在杆端的外力偶Me在圆轴扭转过程中所做的功W算得。当杆在线弹性范围内工作时，在加载过程中，截面B相对于截面A的相对扭转角φ与外力偶矩Me呈线性关系，如图3-15所示。仿照轴向拉压应变能公式的推导方法，即可导出以上应变能表达式。

图3-15　扭转外力偶作用下圆轴的变形及其外力偶所做的功

【例3-5】　如图3-16（a）所示为工程中常用来起缓冲、减振或控制作用的圆柱形密圈螺旋弹簧，承受轴向压（拉）力的作用。设弹簧的平均半径为R，簧杆的直径为d，弹簧的有效圈数（即除去两端与平面接触的部分后的圈数）为n，簧杆材料的剪变模量为G，试在簧杆的斜度α小于5°，且簧圈的平均直径D比簧杆直径d大得多的情况下，推导弹簧的应力和变形的计算公式。

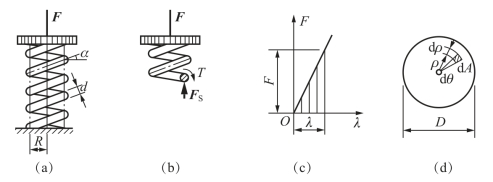
图3-16　圆柱形密圈螺旋弹簧及其受力(www.xing528.com)

解：（1）计算应力

假想用截面法沿簧杆的任一横截面截取其上半部分，并取其为研究对象，其受力如图3-16（b）所示。因α小于5°，为研究方便，可视α为0°，于是簧杆的截面就在包含弹簧截面轴线（即外力F的作用线）的纵向平面内。由平衡方程便可求得截面上的内力分量，通过截面形心的剪力及扭矩分别为FS＝F，T＝FR。

作为近似解，可略去剪力FS所对应的切应力，且D/d很大时，还可略去簧圈的曲率影响。由式（3-8）便可求得簧杆横截面上的最大扭转切应力τmax，即

由上式算出的最大切应力是偏低的近似值。

（2）计算变形

试验表明，在弹性范围内，压力F与变形λ（压缩量）成正比，即F与λ的关系是一条斜直线，如图3-16（c）所示，由此可得外力所做功为

现计算弹簧内的应变能。如图3-16（b）所示，在簧丝横截面上任意点的切应力为

由式（3-25）可得，单位体积的应变能是

因此弹簧的应变能为

式中，V为弹簧的体积。若以dA表示簧丝横截面微面积，ds是簧丝轴线的微长度，则dV＝dA·ds＝ρdθdρds，将式（b）代入式（c），于是有

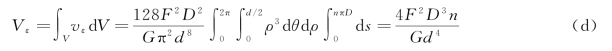
由功能原理可知

由此得弹簧的变形为

式中，R＝，为弹簧圈的平均半径。

令k＝，则式（e）可以写成

可见，k代表弹簧抵抗变形的能力，称为弹簧的刚度，又称为劲度系数。