圆轴扭转应力计算方法

1.几何关系

上述假设说明了圆轴变形的总体情况。为了确定横截面上各点处的应力，需要了解轴内各点处的变形。为此，取相距dx的两个横截面以及夹角无限小的两个径向纵截面，如图3-7（a）所示，从轴内切取一楔形体O1ABCDO2来分析。

根据上述假设，楔形体的变形如图3-7（a）中虚线所示，轴表面的矩形ABCD变为平行四边形ABC′D′，距轴线ρ处的任一矩形abcd变为平行四边形abc′d′，即均在垂直于半径的平面内产生剪切变形。

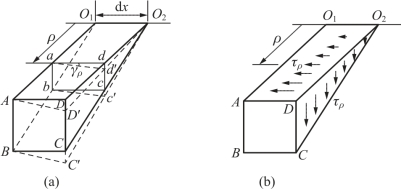
图3-7　圆轴扭转时横截面与纵截面上的切应力分布

设上述楔形体左、右两端横截面间的相对转角即扭转角为dφ，矩形abcd的切应变为γρ，则由图3-7（a）可知

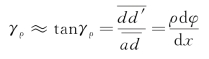
由此得

2.物理方面

由剪切胡克定律可知，在剪切比例极限内，切应力与切应变成正比，所以，横截面上ρ处的切应力为

而其方向则垂直于该点处的半径，如图3-7（b）所示。

上式表明：扭转切应力沿截面径向线性变化，实心与空心圆轴的扭转切应力分布分别如图3-8（a）、（b）所示。

图3-8　实心与空心圆轴扭转切应力的分布图

图3-9　微内力及其对轴心的扭矩

3.静力学方面

如图3-9所示，在距圆心ρ处的微面积dA上作用有微剪力τρdA，它对圆心O的力矩为ρτρdA。在整个横截面上，所有微内力矩之和应等于该截面的扭矩，即(www.xing528.com)

将式（3-5）代入上式，得

式中，积分dA仅与截面尺寸有关，称为截面的极惯性矩，并用Ip表示，即

于是得

式（3-7）即为圆轴扭转变形的基本公式。

最后，将式（3-7）代入式（3-5），得

式（3-8）即圆轴扭转切应力的一般公式。

4.最大扭转切应力

由式（3-8）可知，在ρ＝R即圆截面边缘各点处，切应力最大，其值为

式中，比值Ip/R是一个仅与截面尺寸有关的量，称为扭转截面系数，并用Wp表示，即

于是，圆轴扭转的最大切应力即

可见，最大扭转切应力与扭矩成正比，与扭转截面系数成反比。

圆轴扭转应力公式（3-8）和式（3-10），以及圆轴扭转变形公式（3-7），都是在平面假设的基础上建立的。试验表明，只要圆轴内的最大扭转切应力不超过材料的剪切比例极限，上述公式的计算结果与试验结果一致。这说明，本节所述基于平面假设的圆轴扭转理论是正确的。