薄壁圆筒扭转的切应力优化方式

如图3-1（a）所示的薄壁圆筒，其厚度δ远小于平均半径r（一般要求满足δ≤r/10）。受扭前，在其表面等间距地画上纵向线与圆周线形成矩形方格，然后在圆筒两端缓慢施加一对大小相等、方向相反的扭力偶矩M。圆筒的外部变形如图3-1（b）所示，其现象如下：各圆周线的形状不变，仅绕轴线做相对旋转；而当变形很小时，圆周线的大小与间距也不变，纵向线倾斜同一角度，所有矩形网格均变为同样大小的平行四边形。

图3-1　薄壁圆筒及其扭转变形

以上所述为圆筒的表面变形情况。由于筒壁很薄，也可近似认为筒内变形与筒表面变形相同。于是，如果用相距无限近的两个横截面以及夹角无限小的两个径向纵截面，从圆筒中切取一微体acdb（图3-2），则上述现象表明：微体既无轴向正应变，也无横向正应变，只是相邻横截面a－b与c－d之间发生相对错动，即仅产生剪切变形；而且，所有微体沿圆周方向的剪切变形均相同。

图3-2　薄壁圆筒一微段的变形

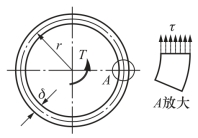
由此可见，在圆筒横截面上的各点处，仅存在垂直于半径方向的切应力τ（图3-3），它们沿圆周分布大小不变，而且，由于筒壁很薄，可近似认为沿壁厚均匀分布。

(www.xing528.com)

图3-3　薄壁圆筒受扭时横截面上的应力分布

设圆筒的平均半径为r，壁厚为δ（图3-4），则作用在微面积dA＝δrdθ上的微剪力为τδrdθ，它对轴线O的力矩为r·τδrdθ。由静力学可知，横截面上所有微力矩之和，应等于该截面的扭矩T，即

由此得

其中，A0为由平均半径围成的圆的面积。式（3-1）即薄壁圆筒扭转切应力的计算公式。精确分析表明，当δ≤时，该公式足够精确，最大误差不超过4.53%。

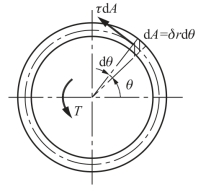
图3-4　薄壁圆筒横截面上的微内力