设受拉杆件上端固定[图2-27(a)],作用于下端的拉力F缓慢地由零增加到F,在应力小于比例极限的范围内,拉力F与伸长Δl的关系是一条斜直线,如图2-27(b)所示,在逐渐加力的过程中,当拉力为F1时,杆件的伸长为Δl1。如果再增加一个dF1,杆件相应的变形增量为d(Δl1)。于是,已经作用于杆件上的F1因位移d(Δl1)而做功,且所做的功为
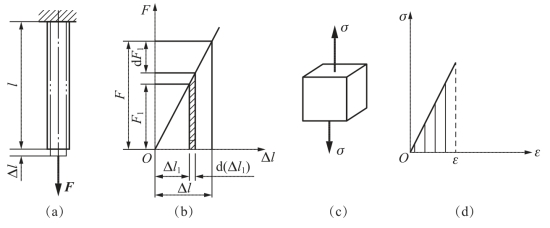
图2-27 受拉杆件变形能和比能
![]()
容易看出dW等于图2-27(b)中画阴影线部分的微分面积。把拉力F看作一系列dF1的积累,则拉力F所做的总功W应为上述微分面积的总和。即W等于F-Δl曲线下面的面积。因为在弹性范围内,F-Δl曲线为一斜直线,故有
![]()
根据功能原理,外力F所做的功在数值上等于杆件内部储存的变形能。因此拉杆的弹性变形能U为
![]()
由胡克定律Δl=![]() 及FN=F,弹性变形能U应为
及FN=F,弹性变形能U应为

变形能的单位和外力功的单位相同,都是焦耳(J)。
若杆的轴力FN,截面面积A和材料弹性模量E分段为常数或连续变化,则变形能的计算式(2-17)可写成下式

若对轴向拉伸(或压缩)杆取单元体表示[图2-27(c)],在线弹性范围内,其应力-应变关系如图2-27(d)所示,则单位体积所储存的变形能为

u称为比能或能密度,其单位是焦耳/米3,记为J/m3。
由式(2-20)可求出拉伸(或压缩)杆的变形能
![]()
式中 V——构件的体积。(https://www.xing528.com)
由U、u的计算式可以看出,变形能是荷载的二次函数,在计算变形能时不满足叠加原理。
利用功能原理可导出的一系列的方法,称能量法,应用能量法可计算任意结构、任意截面、任意点、任意方向的位移。
若结构上只有一个做功力,且仅求力作用点沿力作用方向的位移,可由式(2-17)直接求得。
【例2-9】 简易起重机如图2-28所示。BD杆为无缝钢管,外径90mm,壁厚2.5mm,杆长l=3m,弹性模量E=210GPa。BC是两条横截面面积为171.82mm2的钢索,弹性模量E1=177GPa,荷载F=30kN。若不考虑立柱的变形,试求B点的垂直位移。
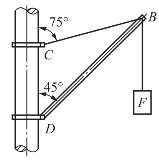
图2-28 简易起重机
解:从三角形BCD中解出BC和CD的长度分别为
![]()
算出BC和BD两杆的横截面面积分别为
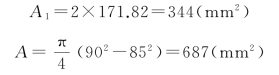
由BD杆的平衡条件,求得钢索BC的拉力为

把简易起重机看作是由BC和BD两杆组成的简单弹性杆系,当荷载F从零开始缓慢地作用于杆系上时,F与B点垂直位移δ的关系是线性的,F所做的功为
![]()
F所做的功在数值上应等于杆系的变形能,亦即等于BC和BD两杆变形能的总和。故
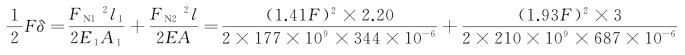
由此求得
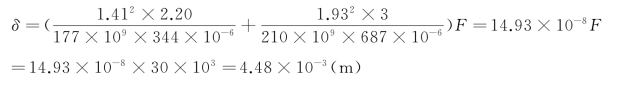
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




