材料拉伸时的力学性质优化分析

为了便于比较不同材料的试验结果，采用国家标准统一规定的标准试件。在试件上取l长作为试验段，称为标距，如图2-11所示。对圆截面试件，标距l与直径d有两种比例，即l＝10d和l＝5d，分别称为10倍试件和5倍试件；对于矩形截面试件，标距l与横截面面积A之间的关系规定为l＝11.3和l＝。对于试件的形状、加工精度、试验条件等在试验标准中都有具体规定。

图2-11　圆截面试件

试验时使试件受轴向拉伸，观察试件从开始受力直到拉断的全过程，了解试件受力与变形之间的关系，以测定材料力学性能的各项指标。

1.低碳钢在拉伸时的力学性能

低碳钢一般是指碳的质量分数在0.3%以下的碳素钢。实验时把低碳钢试件装在试验机上，然后缓慢加载。试验机的示力盘上指出一系列拉力F的数值，对应着每一个拉力F，同时可测出试件标距l的伸长量Δl。以纵坐标表示拉力F，横坐标表示伸长量Δl。根据测得的一系列数据，做出表示F和Δl关系的曲线，如图2-12所示，称为拉伸图或F－Δl曲线。

F－Δl曲线与试件的尺寸有关。为了消除试件尺寸的影响，拉力F除以试件横截面的原始面积A，得出试件横截面上的正应力σ＝F/A；同时，伸长量Δl除以标距的原始长度l，得到试件在工作段内的应变ε＝Δl/l。以σ为纵坐标、ε为横坐标，作图表示σ与ε的关系（图2-13），称为应力－应变图或σ－ε曲线。

图2-12　F－Δl曲线

图2-13　σ－ε曲线

根据试验结果，低碳钢的力学性能大致如下：

（1）弹性阶段。在拉伸的初始阶段，σ与ε的关系为直线Oa，这表示在这一阶段内σ与ε成正比，即

或者把它写成等式

这就是拉伸或压缩时的胡克（Hooke）定律。式中，E为与材料有关的比例常数，称为弹性模量，它表示材料的弹性性质，是材料抵抗弹性变形的能力，E的值可通过实验测定。因为应变ε没有量纲，故E的量纲与σ相同。由公式（2-7），并从σ－ε曲线的直线部分看出

所以E是直线Oa的斜率。直线Oa的最高点a所对应的应力，用σp表示，称为比例极限。可见，当应力低于比例极限时，应力与应变成正比，材料服从胡克定律。

应力超过比例极限后，从a点到b点，σ与ε之间的关系不再是直线，但变形仍然是弹性，即解除拉力后变形将完全消失。b点所对应的应力是材料只出现弹性变形的极限值，称为弹性极限，用σe表示。在σ－ε曲线上，a、b两点非常接近，所以工程上对弹性极限和比例极限并不严格区分。因而也经常说，应力低于弹性极限时，应力与应变成正比，材料服从胡克定律。

在应力大于弹性极限后，如再解除拉力，则试件变形的一部分随之消失，但还遗留下一部分不能消失的变形，前者是弹性变形，而后者就是塑性变形或残余变形。

（2）屈服阶段。当应力超过b点增加到某一数值时，应变有非常明显的增加，而应力先是下降，然后做微小的波动，在σ－ε曲线上出现接近水平线的小锯齿形线段。这种应力基本保持不变，而应变显著增加的现象，称为屈服或流动。在屈服阶段内的最高应力和最低应力分别称为上屈服点和下屈服点。上屈服点的数值与试件形状、加载速度等因素有关，一般是不稳定的。下屈服点则有比较稳定的数值，能够反映材料的性能，通常把下屈服点称为屈服点或屈服极限，用σs来表示。

表面磨光的试件屈服时，表面将出现与轴线大致成45°的条纹，如图2-14所示，这是由于材料内部晶格之间相对滑移而形成的，称为滑移线。因为拉伸时在与轴线成45°的斜截面上，切应力为最大值，可见屈服现象的出现与最大切应力有关。

图2-14　表面磨光的试件

材料屈服时出现了显著的塑性变形，而构件出现塑性变形将影响机器的正常工作，所以屈服点σs是衡量材料强度的重要指标。

（3）强化阶段。经过屈服阶段后，材料又恢复了抵抗变形的能力，要使它继续变形必须增加拉力。这种现象称为材料的强化。在图2-13中，强化阶段中的最高点e所对应的应力σb是材料所能承受的最大应力，称为强度极限或抗拉强度。它是衡量材料强度的另一重要指标。在强化阶段中，试件的横向尺寸明显缩小，其变形绝大部分是塑性变形。试件在前三个阶段中的变形是均匀的。

（4）局部变形阶段。过e点后，在试件的某一局部范围内，横向尺寸突然急剧缩小，形成缩颈现象[图2-15（a）]。由于在缩颈部分横截面面积迅速减小，使试件继续伸长所需要的拉力也相应减小，在应力-应变图中，用横截面原始面积A算出的应力σ＝F/A随之下降，降落到f点，试件被拉断，断口为“杯状”[图2-15（b）]。(www.xing528.com)

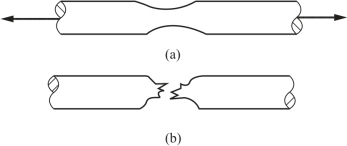
图2-15　局部变形

（5）伸长率和断面收缩率。试件拉断后，由于保留了塑性变形，试件长度由原来的l变为l1。用百分比表示的比值

称为伸长率。塑性变形（l1－l）越大，δ也就越大。因此，伸长率是衡量材料塑性的指标。低碳钢的伸长率很高，平均值为20%～30%，这说明低碳钢的塑性性能很好。

工程上通常按伸长率的大小把材料分成两大类：δ≥5%的材料称为塑性材料，如碳钢、黄铜、铝合金等；而δ＜5%的材料称为脆性材料，如灰铸铁、玻璃、陶瓷等。

原始横截面面积为A的试件，拉断后缩颈处的最小截面面积为A1，用百分比表示的比值

称为断面收缩率。Ψ也是衡量材料塑性的指标。

（6）卸载定律及冷作硬化。在低碳钢的拉伸试验中，如把试件拉到超过屈服点的d点（图2-13），然后逐渐卸掉拉力，应力和应变关系将沿着斜直线dd′回到d′点，斜直线dd′近似平行于Oa。这说明：在卸载过程中，应力和应变按直线规律变化，且在卸载过程中的弹性模量和加载时相同，这就是卸载定律。拉力完全卸掉后，在应力-应变图中，d′g表示消失了的弹性应变εe，而Od′表示残余的塑性应变εp，而且总应变ε＝εe＋εp。

卸载后，如在短期内再次加载，则应力和应变大致沿卸载时的斜直线dd′变化，直到d点后，又沿曲线def变化。可见在再次加载时，直到d点以前材料的变形是弹性的，过d点后才开始出现塑性变形。比较图2-13中的Oabcdef和d′def两条曲线，可见在第二次加载时，其比例极限得到了提高，但塑性变形和伸长率有所降低，这种现象称为冷作硬化。冷作硬化现象经退火后又可消除。

工程上常利用冷作硬化来提高材料的弹性极限，如起重用的钢索和建筑用的钢筋，常用冷拔工艺以提高强度。又如对某些零件进行喷丸处理，使其表面发生塑性变形，形成冷硬层，以提高零件表面层的强度；但另一方面，零件初加工后，由于冷作硬化使材料变脆变硬，给下一步加工造成困难，且容易产生裂纹，往往需要退火，以消除冷作硬化的影响。

2.其他塑性材料在拉伸时的力学性能

工程上常用的塑性材料，除低碳钢外，还有中碳钢、某些高碳钢和合金钢、铝合金、青铜、黄铜等。图2-16所示为几种塑性材料的σ－ε曲线。其中有些材料，如16Mn钢和低碳钢一样，有明显的弹性阶段、屈服阶段、强化阶段和局部变形阶段。有些材料没有屈服阶段和局部变形阶段，只有弹性阶段和强化阶段。

对于没有明显屈服阶段的塑性材料，通常以产生0.2%的塑性应变所对应的应力作为屈服强度或条件屈服极限，用σ0.2来表示，如图2-17所示。

在各类碳素钢中，随碳含量的增加，屈服点和强度极限相应提高，但伸长率降低。例如合金钢、工具钢等高强度钢，其屈服点较高，但塑性性质较差。

图2-16　几种塑性材料的σ－ε曲线

图2-17　用σ0.2来表示屈服强度

3.铸铁在拉伸时的力学性质

取标准试件，如图2-11所示。灰铸铁拉伸时的应力-应变关系是一段微弯曲线，如图2-18（a）所示，没有明显的直线部分，没有屈服和缩颈现象，拉断前的应力和应变都很小，伸长率也很小，断口平齐，如图2-18（b）所示，断口处的横截面面积几乎没有变化，是典型的脆性材料。

由于铸铁的σ－ε曲线没有明显的直线部分，弹性模量E的数值随应力的大小而变。但在工程中，铸铁的拉应力不能很高，在较低的拉应力下，则可近似地认为服从胡克定律。通常取σ－ε曲线的割线代替曲线的开始部分，并以割线的斜率作为弹性模量，称为割线弹性模量，如图2-18（a）所示。

铸铁拉断时的最大应力即强度极限。因为没有屈服现象，强度极限σb是衡量强度的唯一指标。铸铁等脆性材料的抗拉强度很低，所以不宜作为抗拉零件。

图2-18　灰铸铁拉伸时的应力－应变关系

铸铁经球化处理成为球墨铸铁后，力学性能有显著变化，不但有较高的强度，还有较好的塑性性能。国内有不少工厂成功地用球墨铸铁代替钢材制造曲轴、齿轮等零件。