材料力学中的基本假设

实际工程中的任何构件、机械或结构都是变形体，或称为变形固体。变形固体在外力及其他外部因素的作用下，其本身的性质和行为可能比较复杂。材料力学不可能同时考虑各种因素的影响，而只能保留所研究问题的主要方面，略去次要因素，对变形固体做某些假设，即将复杂的实际物体抽象为具有某些主要特征的理想固体，以便于进行强度、刚度和稳定性的理论分析。通常，在材料力学中，对变形固体做如下假设。

1.连续性假设

连续是指在物体或构件所占据的空间内没有空隙，处处充满了物质，即认为物体或构件是密实的。且认为物体在变形后仍保持这种连续性，即受力变形后既不产生新的空隙或孔洞，也不出现重叠现象。这样可以保证物体或构件中的一些物理量（如任意一点的位移等）是连续的，因而可以用坐标的连续函数来描述，便于利用微积分等数学工具。广泛的实验与工程实践证实，由此假定所做的力学分析是可行的。

2.均匀性假设

材料在外力作用下所表现出来的性能，称为材料的力学性能。在材料力学中，假设材料的力学性能与其在构件中的位置无关，即认为材料是均匀的。按此假设，从构件内部任何部位所切取的微小单元体（简称为单元体）都具有与构件完全相同的性能。同样，通过试样所测得的力学性能也可用于构件内的任何部位。

对于实际材料，其基本组成部分的力学性能往往存在不同程度的差异。例如，金属是由无数微小晶粒组成，而各个晶粒的力学性能不完全相同，晶粒交界处的晶界物质与晶粒本身的力学性能也不完全相同。但是，由于构件的尺寸远大于其组成部分的尺寸（例如1mm3的钢材中包含数万甚至数十万个晶粒），因此，按照统计学观点，仍可将材料看成均匀的。

3.各向同性假设

假设材料在各个不同方向具有相同的力学性质，即认为其是各向同性的。沿各个方向具有相同力学性能的材料称为各向同性材料，如玻璃。金属的各个晶粒均属于各向异性体，但由于金属构件所含晶粒极多，且在构件内随机排列，宏观上仍可将金属看成各向同性材料。因此，在各向同性材料中，表征材料特性的力学参量（如弹性模量等）与方向无关，为常量。应指出，如果材料沿不同方向具有不同的力学性质，则称为各向异性材料。木材、复合材料是典型的各向异性材料。

以上针对材料的三个假设是材料力学普遍采用的前提假设。除以上三个假设外，材料力学还常常依据小变形假设来推导有关定理或结论。所谓小变形假设，是指所研究的构件在外荷载作用下发生的变形都是微小的，在很多情况下需要用专门的仪器才能观察到。比如结构工程中的梁，它在荷载作用下整个跨度上产生的最大位移比梁横截面的尺寸小很多。(www.xing528.com)

绝大多数工程构件在实际工作状态中所发生的变形都属于小变形。这也是采用小变形假设的合理之处。

采用小变形假设可以使分析过程得以简化，这可以从两个方面说明。

第一，原始尺寸原理。对变形体的分析和计算可以在未变形的构形（指形状和尺寸）上进行，这可用图1-7加以说明。图1-7是一个简单桁架，其中一根杆件是竖直的，另一根是倾斜的。如图1-7（a）所示，若在结点上作用一个竖向集中力，按理论力学中静力学的分析，斜杆是所谓零杆，即内部不存在作用力。

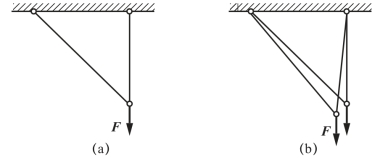
图1-7　两种计算构形

当实际作用集中力并考虑到构件的变形后，平衡的形态将如图1-7（b）所示。严格意义上说，斜杆不再是零杆，因而两杆内部的力和变形都不再如图1-7（a）的分析那么简单。但是，由于杆件发生的变形是微量的，由分析可知，按照图1-7（b）计算的位移与图1-7（a）的计算结果之差是比杆件产生的小变形还要高阶的微量，因此可以忽略不计，即认为斜杆是零杆。一般地，在材料力学课程中，除了少数几处特别需要并加以声明的情况，总是在未变形的原始构形上进行平衡分析。这种考虑弹性构件的内力与外力平衡时，在未变形的原始构形上进行分析的方法称为原始尺寸原理。

第二，线性化原理。在许多分析过程中，如果能够确定某些无量纲量是高阶微量，本书都将适时地将其舍去，从而使分析的方程线性化。例如，在研究构件的位移和变形的几何关系时，构件上一点的位移常常是一条弧线（二次或更高次），为简化分析和计算，常用直线（切线或垂线）（线性）代替。又如，在已经确认x是无量纲量的微量的前提下，sinx、tanx均可以简化为x，而cosx则可以简化为1。诸如此类的处理可以简化分析计算过程，且由于工程中的很多问题都是小变形问题，所以可以保证工程精度的要求。

提示：（1）虽然材料力学中的变形是微小的，但其作用是巨大的。如何依据所观察到的现象，正确地对变形提出假设，并据此寻找变形量之间的关系，是很多材料力学问题的基础。（2）材料力学主要是用线性化的手段处理非线性问题，所以材料力学的分析方法主要为一阶分析方法。这既是材料力学的优势（计算简洁又可满足大多数工程精度要求），也是它的劣势（不能进行高阶精度的分析）。