MATLAB实现线性二次型Gauss最优控制器

考虑系统随机输入噪声与随机量测噪声的线性二次型最优控制叫做线性二次型高斯（Gauss）最优控制，即LQG控制。必须注意，线性二次型高斯最优控制是输出反馈控制，即设计的LQG控制器对原系统是反馈控制器。

在MATLAB工具箱里，有特别提供的函数reg（）求解LQG最优控制。函数调用格式为

rsys=reg（sys，K，L）其中，输入参数sys为系统状态空间模型；K为由函数lqr（）求得的最优状态反馈增益矩阵；L为函数lqe（）求得的Kalman滤波器状态估计增益矩阵。输出参数rsys为系统LQG控制器的状态空间模型。

为方便计算，作者编制了求解连续系统线性二次型LQG最优控制器的函数lqgreg.m。

【例15-7】 已知系统的状态方程、y=[0.51.25]x+v，二次型调节器性能指标为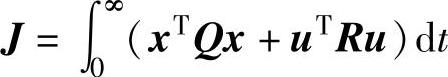，式中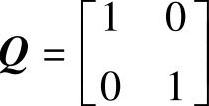，R=1。输入噪声与量测噪声的有关参数分别为Q₀=1，R₀=1。要求：1）对原系统进行阶跃给定输入的仿真；2）试设计LQG控制器，并对LQG最优控制系统进行阶跃给定输入的仿真。

解：1）用以下MATLAB程序对原系统进行阶跃给定输入的仿真：

clear；A=[2-2；20]；B=[2；0]；C=[0.51.25]；

D=[0]；s=ss（A，B，C，D）；step（s），grid；

程序执行后得到原系统的给定输入阶跃响应仿真曲线，如图15-11所示。由曲线可以看到，原系统的阶跃响应为发散的振荡，即系统是不稳定的。

2）给出以下调用自编函数lqgreg.m的MATLAB程序解算LQG控制器。

clear；A=[2-2；20]；B=[2；0]；C=[0.51.25]；D=[0]；

R=1；Q0=1；R0=1；t=0：0.01：8；

[lqgsys]=lqgreg（A，B，C，D，R，Q0，R0，t）；

程序执行后得到LQG控制器：

(www.xing528.com)

程序执行后还绘制出LQG最优控制的系统单位阶跃响应曲线，如图15-12所示。

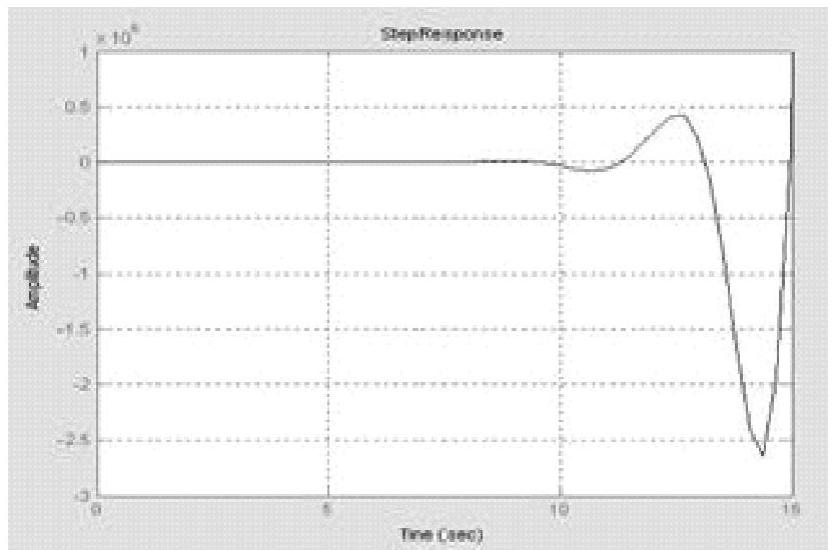
图15-11 原系统单位阶跃响应曲线

图15-12　LQG最优控制阶跃响应曲线

由LQG最优控制的阶跃响应仿真曲线可以看到，不但系统变稳定了，而且阶跃响应仅稍有超调与微弱振荡，曲线是很理想的。这比不稳定的原系统确是最优控制的效果。

【例15-8】 试对可控直流电源供电给直流电机系统结构模型sx2L1503.mdl即图15-5进行LQG最优控制。

解：给出以下调用自编函数lqgreg.m的MATLAB程序解算LQG控制器。

clear；[A，B，C，D]=linmod2（sx2L1503）；R=1；Q0=1；R0=1；

t=0：0.01：1；[lqgsys]=lqgreg（A，B，C，D，R，Q0，R0，t）；

程序执行后得到LQG控制器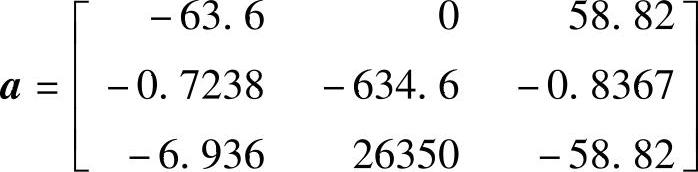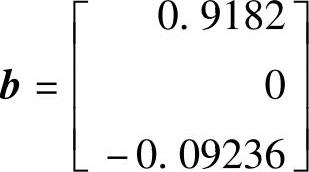：，，c=[0.723835.750.8367]，d=0

程序执行后还绘制出LQG最优控制的系统单位阶跃响应曲线，如图15-13所示。由图15-13可见，LQG最优控制的系统与经Kalman滤波的系统，两者闭环后其单位阶跃给定响应基本一致，仿真曲线为几乎是立即响应的阶跃方波，确实非常理想。再仔细比较两者，似乎LQG最优控制比Kalman滤波的效果还要好。

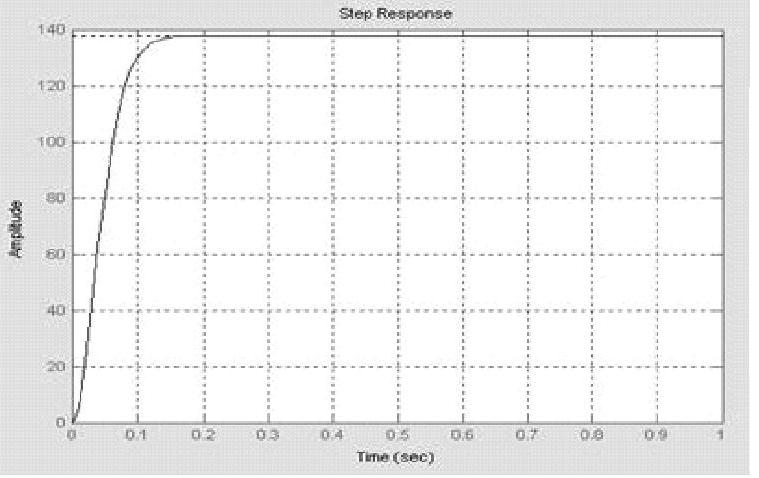
图15-13　LQG最优控制系统阶跃响应曲线