MATLAB实现最优观测器（Kalman滤波）效果优化

对于连续时不变系统，其状态方程与量测方程分别为

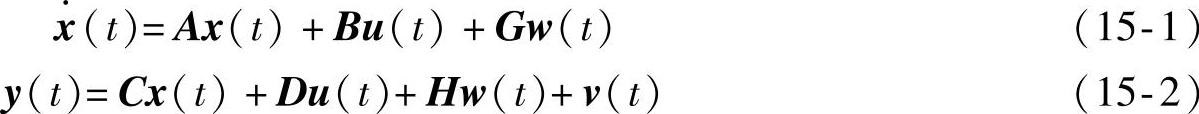
系统的Kalman滤波器就是最优观测器。利用Kalman滤波器对系统进行最优控制是非常有效的。MATLAB系统特别开发有求解Kalman滤波器的函数kalman（）。函数调用格式为

[Kest，L，P]=kalman（sys，Q，R，N）

其中，输入参数sys为连续或离散系统带扰动的状态空间模型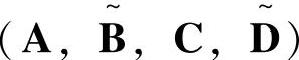，当模型有两个输入时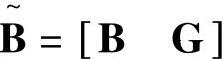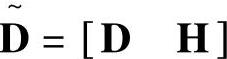，，；Q为模型噪声的协方差矩阵；R为量测噪声的协方差矩阵；N为可选项，它对应模型噪声与量测噪声的相关项。输出参数Kest为Kalman滤波器的状态估计器，其动态方程为

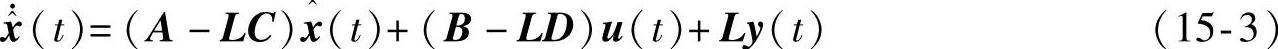
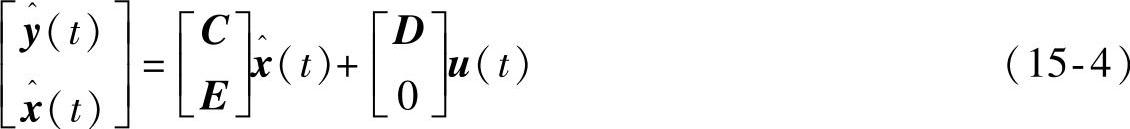
式中，L为Kalman滤波器的增益矩阵；P为对应的Riccati方程的解，即估计误差的协方差。MATLAB还提供过两个配合使用的函数lqe（）与estim（）来求解系统的Kalman滤波器。

函数lqe（）的调用格式为

[L，P，E]=lqe（A，G，C，Q，R，N）

其中，输入参数A、G、C为式（15-1）与式（15-2）中的对应参量；Q为模型噪声的协方差矩阵；R为量测噪声的协方差矩阵；N为可选项，它对应模型噪声与量测噪声的相关项。输出参数L为Kalman滤波器的增益矩阵；P为对应的Riccati方程的解，即估计误差的协方差；E为估计器的闭环特征值。函数estim（）的调用格式为

est=estim（sys，L）

这个函数用来生成连续系统的Kalman滤波器，即系统的状态估计器est。输入参数sys为连续系统带扰动的状态空间模型，输入参数L为函数lqe（）求出的Kalman滤波器的增益矩阵。

对于连续系统，用函数kalman（）计算的Kalman滤波器的状态估计器Kest与用函数es-tim（）求出的Kalman滤波器est，两者应相等。

【例15-5】 已知单位负反馈连续系统受控对象与串联校正装置的传递函数为

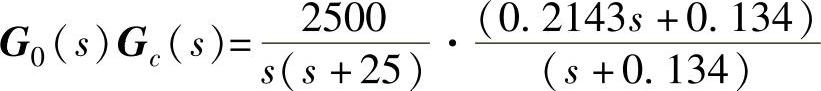
设模型噪声协方差矩阵Q=1、量测噪声协方差矩阵R=0.01，试求系统Kalman滤波器增益矩阵L、系统估计误差协方差P以及系统的Kalman（最优）滤波器。

解：给出调用系统函数kalman.m与estim.m的MATLAB程序求解。(www.xing528.com)

clear；n1=[002500]；d1=[1250]；sys1=tf（n1，d1）；G1=ss（sys1）；

n2=[0.21430.134]；d2=[10.134]；sys2=tf（n2，d2）；G2=ss（sys2）；

G3=G1∗G2；G=feedback（G3，1）；q=1；r=0.01；

[Kest，L，P]=kalman（G，q，r），est=estim（G，L），

程序运行后得到系统Kalman滤波器的增益矩阵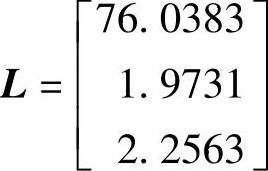、系统估计误差的协方差，计算表明，用函数kalman.m计算的Kalman滤波器的状态估计器Kest与用函数estim.m求出的Kalman滤波器est是相等的。

【例15-6】 续【例15-3】，已知可控直流电源供电给直流电机的系统结构图如图15-5所示。试对系统进行Kalman滤波器的设计并对经Kalman滤波后的系统闭环进行阶跃响应仿真。

解：给出调用自编函数lqkalm.m的程序进行Kalman滤波器的设计。

clear；[A，B，C，D，]=linmod2（sx2L1503）；

R=1；Q0=1e-4；R0=1e-5；；t=0：0.001：0.3；

[L，P，kalmsys]=lqkalm（A，B，C，D，R，Q0，R0，t）；

程序运行后，可得到Kalman滤波器的增益矩阵L与估计误差的协方差P分别为

程序运行后还得到经Kalman滤波后系统闭环单位阶跃响应仿真曲线，如图15-10所示。

由图15-10可见，经Kalman滤波后，系统闭环单位阶跃给定响应是非常理想的，仿真曲线为几乎立即响应的阶跃方波，只稍微有一点点超调，尔后曲线趋于水平。

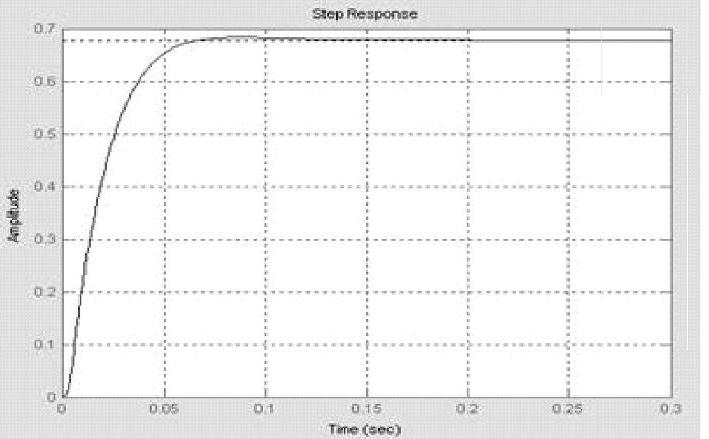
图15-10 经Kalman滤波后的单位阶跃响应曲线