MATLAB实现离散系统线性二次型最优控制

对象为离散系统的是离散系统线性二次型最优控制。在这里，需要复习《控制系统MATLAB计算及仿真》中相应的关系式，并要复习MATLAB求解离散系统线性二次型状态调节器的函数。其函数有dlqr（）与dlqry（）。函数的调用格式为

[K，S，E]=dlqr（A，B，Q，R，N）

[K，S，E]=dlqry（A，B，C，D，Q，R，N）

其中，输入参数A为系统的状态矩阵；B为系统的输入矩阵；Q为给定的正定或半正定实对称矩阵；R为给定的正定实对称矩阵；N代表更一般化性能指标中交叉乘积项的加权矩阵。输出参数K为离散最优反馈增益矩阵；S为对应Riccati方程的唯一正定解P；E为A-BK的特征值。

函数dlqry（）用来求解二次型状态调节器的特例，即用输出反馈替代状态反馈。【例15-4】 续【例15-3】，已知如图15-5所示可控直流电源供电给直流电机的系统。试对系统设计数字最优控制系统（即计算状态反馈增益矩阵）并求闭环离散系统的阶跃响应。

状态反馈时、R=[1]。

解：需要认真复习连续系统离散化的函数命令与状态反馈的公式。

clear；[a1，b1，c1，d1]=linmod2（sx2L1503）；

Q=diag（[101101]）；R=[1]；

[a，b]=c2d（a1，b1，0.1）；c=c1；d=d1；

A=[a zeros（3，1）；-c∗a 1]；(www.xing528.com)

B=[b；-c∗b]；Kx=dlqr（A，B，Q，R）

k1=-Kx（2）；k2=Kx（1）；axc=A-B∗Kx；

bxc=[0；0；0；1]；cxc=[0100]；dxc=[0]；

dstep（axc，bxc，cxc，dxc，1，10），grid；

程序运行后得到数字最优控制系统的状态反馈增益矩阵

K=[0.10366.56960.1451-0.0059]

程序运行后还绘制闭环离散系统阶跃响应曲线，如图15-9所示。

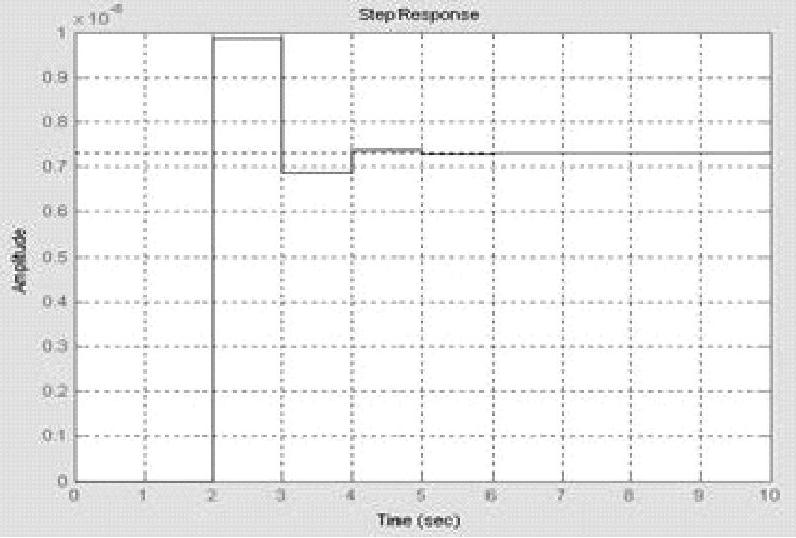
图15-9 闭环离散系统的阶跃响应曲线