李雅普诺夫第二方法用李雅普诺夫函数V(x)=xTPx判断系统在原点x=0处的平衡状态有以下4个定理。
定理1 设系统的状态方程为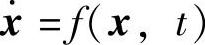 ,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),并且满足V(x,t)是正定的、
,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),并且满足V(x,t)是正定的、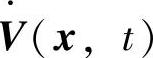 是负定的,则系统在原点处的平衡状态是一致渐近稳定的。
是负定的,则系统在原点处的平衡状态是一致渐近稳定的。
又当‖x‖→∞时,有V(x,t)→∞,则在原点处平衡状态是在大范围内一致渐近稳定的。
定理2 设系统的状态方程为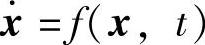 ,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),并且满足V(x,t)是正定的、
,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),并且满足V(x,t)是正定的、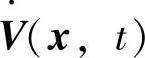 是半负定的、
是半负定的、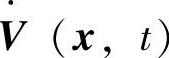 在x≠0时不恒等于0,则系统在原点处的平衡状态是大范围渐近稳定的。
在x≠0时不恒等于0,则系统在原点处的平衡状态是大范围渐近稳定的。
定理3 设系统的状态方程为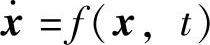 ,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),若V(x,t)是正定的、
,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t),若V(x,t)是正定的、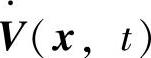 是半负定的,则系统在原点处的平衡状态是一致稳定的。
是半负定的,则系统在原点处的平衡状态是一致稳定的。
定理4 设系统的状态方程为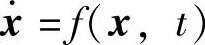 ,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t)若V(x,t)是正定的、
,其平衡状态为f(0,t)=0。如果存在一个具有连续一阶偏导数的标量函数V(x,t)若V(x,t)是正定的、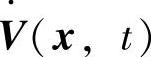 也是正定的,则系统在原点处的平衡状态是不稳定的。
也是正定的,则系统在原点处的平衡状态是不稳定的。
为方便计算,作者编制了一个计算系统李雅普诺夫函数的函数lyaeq.m。请看示例。
【例14-31】 已知线性定常连续系统动态方程为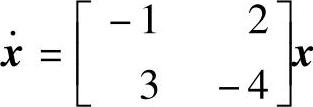 ,试求解李雅普诺夫方程,并判定系统的渐近稳定性。
,试求解李雅普诺夫方程,并判定系统的渐近稳定性。
解:给出以下调用自编函数lyaeq.m的MATLAB程序求解。
clear;A=[-12;3-4];Q=[10;01];key=1;(https://www.xing528.com)
[FQ,P,Vx]=lyaeq(key,A,Q);
程序运行后得到(1)系统特征根λ1=0.3723>0、λ2=-5.3723<0,故系统原点的平衡状态是不稳定的;(2)矩阵A非奇异,坐标原点是系统唯一的平衡状态;(3)李雅普诺夫方程的解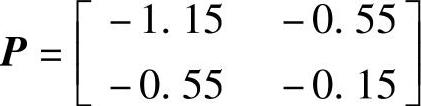 ;(4)矩阵A的各主子行列式detP11=-1.15<0与detP=-0.13<0,矩阵A是负定矩阵,故系统在平衡点处不是渐近稳定的;(5)李雅普诺夫函数
;(4)矩阵A的各主子行列式detP11=-1.15<0与detP=-0.13<0,矩阵A是负定矩阵,故系统在平衡点处不是渐近稳定的;(5)李雅普诺夫函数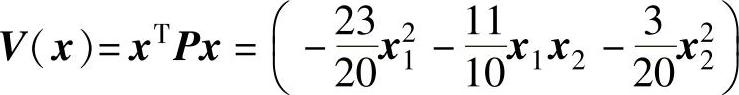 ;(6)
;(6)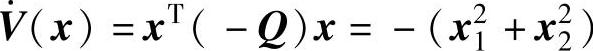 。
。
【例14-32】 已知线性定常离散系统动态方程为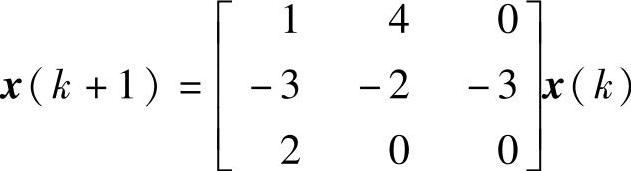 ,试求解李雅普诺夫方程,并判定系统的渐近稳定性。
,试求解李雅普诺夫方程,并判定系统的渐近稳定性。
解:给出以下调用自编函数lyaeq.m的MATLAB程序求解。
clear;A=[140;-3-2-3;200];
Q=[100;010;001];key=2;
[FQ,P,Vx]=lyaeq(key,A,Q);
程序运行后得到(1)系统特征根λ1.2=0.5±j3.4278、λ3=-2均在单位圆外,故系统原点的平衡状态是不稳定的;(2)矩阵A非奇异,坐标原点是系统唯一的平衡状态;(3)李雅普诺夫方程的解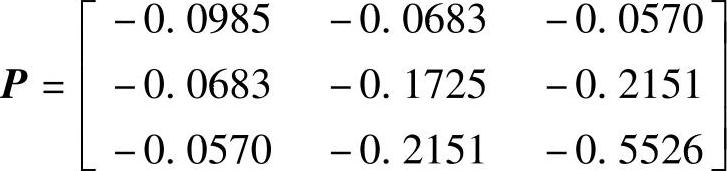 ;(4)矩阵A的各主子行列式detP11=-0.0985<0与detP=-0.0034<0,矩阵A是负定矩阵,故系统在平衡点处不是渐近稳定的;(5)
;(4)矩阵A的各主子行列式detP11=-0.0985<0与detP=-0.0034<0,矩阵A是负定矩阵,故系统在平衡点处不是渐近稳定的;(5)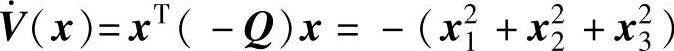 ;(6)李雅普诺夫函数V(x)=xTPx
;(6)李雅普诺夫函数V(x)=xTPx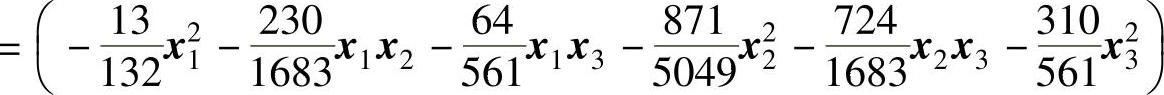 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




