当观测器的维数等于原系统状态向量的维数时叫做全维观测器。所谓状态降维观测器,就是观测器维数在低于原系统状态向量维数时,也能对原系统状态做出最佳估计的观测器。对于一个n维的可观测系统:

式中,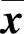 为n维向量,u为p维向量,
为n维向量,u为p维向量,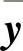 为q维向量,
为q维向量, 、
、 、
、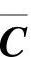 分别为(n×n)维、(n×p)维、(q×n)维矩阵。当
分别为(n×n)维、(n×p)维、(q×n)维矩阵。当 满行秩(即
满行秩(即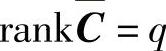 )时,可以定义一种非奇异线性变换
)时,可以定义一种非奇异线性变换

式中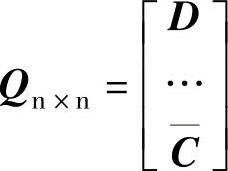
请注意,式中D是使Q非奇异的(n-q)×n维任意矩阵。
系统 经非奇异线性变换后的系统{A,B,C}:
经非奇异线性变换后的系统{A,B,C}:

式中 
即为把x分解为x1与x2两部分,其中x2是q个直接由输出测得的状态变量。变换后系统中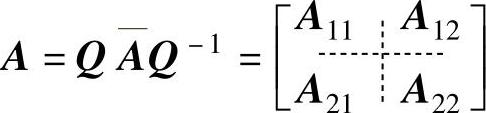 、
、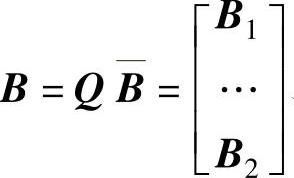 、
、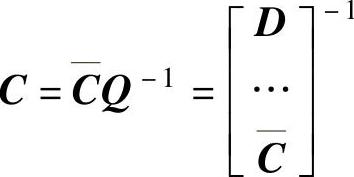 ,由恒等式
,由恒等式
对比这两式可得 C=[0 E]
故有 
式中,x1为(n-q)维列向量;x2为q维列向量;A11为(n-q)×(n-q)维矩阵;A12为(n-q)×q维矩阵;A21为q×(n-q)维矩阵;A22为q×q维矩阵;B1为(n-q)×p维矩阵;B2为q×p维矩阵。
因为系统 可观测,经线性坐标变换后的系统{A,B,C}仍为可观测系统。
可观测,经线性坐标变换后的系统{A,B,C}仍为可观测系统。
由式(14-7)可以看出,通过直接测量输出y,已可得到系统的部分状态x2,现在只要设计出能估计状态x1的(n-q)维观测器,它就是原系统{A,B,C}的降维观测器了。这个(n-q)维观测器通常称为龙伯格观测器。
考虑y=x2、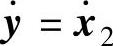 并计及式(14-7),式(14-6)可以改写成如下形式:
并计及式(14-7),式(14-6)可以改写成如下形式:

令v=A12y+B1u、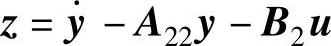
式(14-8)可写为 
式(14-9)是一个(n-q)维子系统动态方程,第一式是状态方程,第二式是输出方程。z是该子系统的q维输出向量,x1是(n-q)维状态变量,v是(n-q)维输入向量,A11是(n-q)×(n-q)维状态矩阵,A21是q×(n-q)维输出矩阵。
与构成全维观测器的方法相同,构成带降维状态观测器的(n-q)维子系统图如图14-9所示。
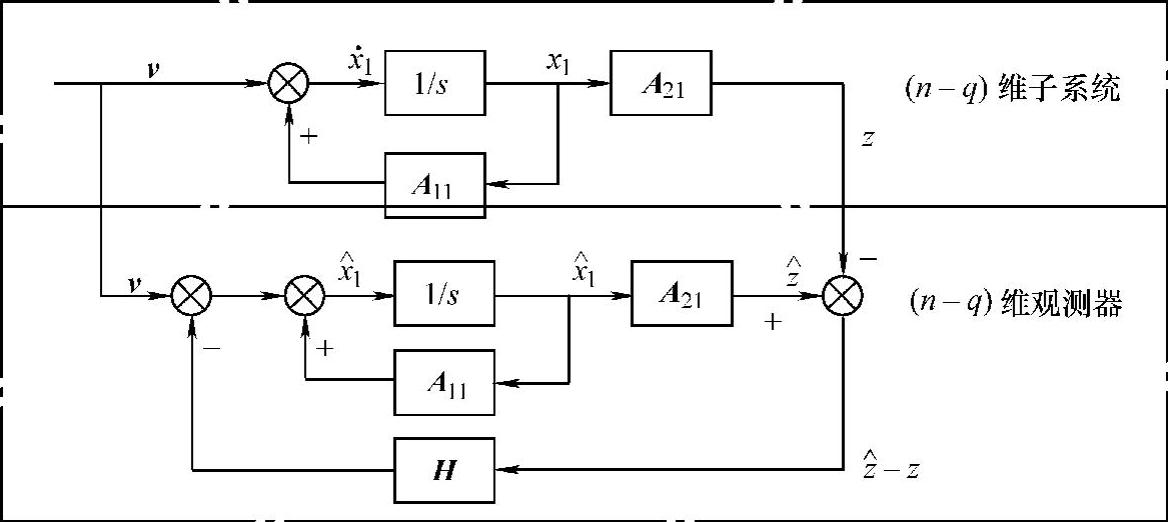
图14-9 用降维观测器实现状态反馈的系统模型原理图
由图14-9可得降维状态观测器(龙伯格观测器)的动态方程为

式中,观测器输出反馈阵H为(n-q)×q维矩阵,观测器的输出就是x1。
考虑v=(A12y+B1u)、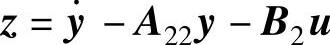 ,式(14-10)所示的降维观测器可写成
,式(14-10)所示的降维观测器可写成
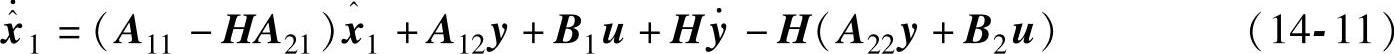
式中,(A11-HA21)为系统降维状态观测器矩阵。降维状态观测器的极点由特征方程

或者式
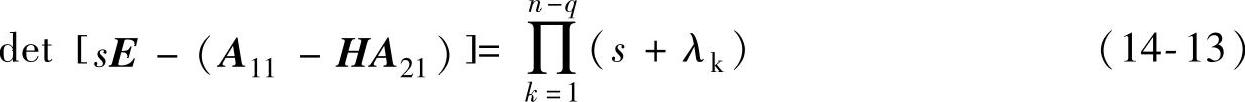
决定。式中,E为单位矩阵。若是给定降维状态观测器的极点,则可由式(14-12)或式(14-13)解算出观测器输出反馈矩阵H。
还需指出,式(14-11)中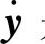 是不能直接量测到的,为避免应用
是不能直接量测到的,为避免应用 ,特作如下变量变换:
,特作如下变量变换:

所以降阶观测器为

这样,系统{A,B,C}的状态估计则按下式求得

自动控制理论中已经说明,只要子系统(A11,A21)完全能观测,H就一定存在。由式(14-12)或式(14-13)算出矩阵H后,状态观测器式(14-15)即可解得。
若要绘制带降维观测器的系统模型图,还需要将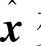 变换回到
变换回到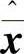 状态空间,于是又有
状态空间,于是又有

式中, 、
、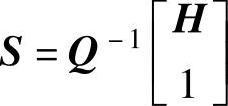 。为方便计算,作者编制了计算降维状态估计器的函数reduest.m。请看示例。
。为方便计算,作者编制了计算降维状态估计器的函数reduest.m。请看示例。
【例14-29】 已知系统动态方程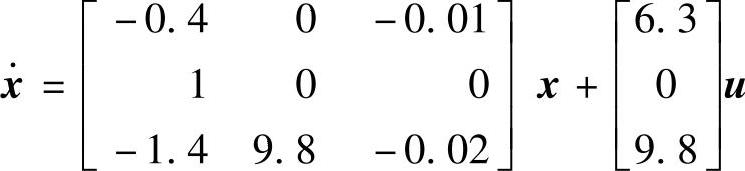 、y=[001]x。
、y=[001]x。
1)计算系统的单位阶跃响应;2)计算系统可控标准型动态方程,并验证线性变换传递函数的不变性;3)绘制可控标准型系统仿真模型,并对其进行单位阶跃响应仿真;4)判别系统可控性,并求状态反馈增益矩阵K,要求系统闭环极点为λ1=-2、λ2.3=-1±j;5)要求系统闭环极点不变,求系统状态观测器的增益矩阵Kh;6)判别系统的可观性,并设计状态观测器;7)绘制带状态观测器及其反馈增益矩阵Kh的可控标准型系统仿真模型,并对其进行单位阶跃响应仿真;8)计算系统降维状态观测器,要求系统闭环极点为λ1.2=-3±j3;9)绘制带降维状态观测器及其反馈增益矩阵Kh的可控标准型系统仿真模型,并进行仿真。
解:1)求可控标准型系统空间动态方程。
clear;A1=[-0.40-0.01;100;-1.49.8-0.02];
B1=[6.3;0;9.8];C1=[001];D=0;
[P,A,B,C]=consta(A1,B1,C1);
程序运行表明,原系统与可控标准型系统都是可控的,计算得到可控标准型
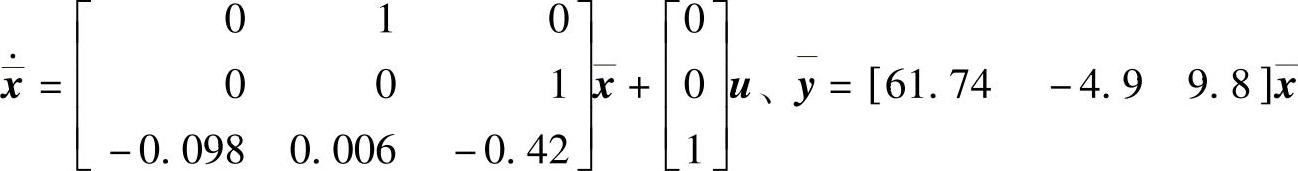
给出以下调用自编函数tran01.m的程序解算可控标准型系统对应的传递函数矩阵G(s)。
clear;syms s t;A=[010;001;-0.09800.0060-0.4200];
B=[0;0;1];C=[61.74-4.99.8];D=0;[invsea,G]=tran01(A,B,C,D);
程序运行后得到传递函数矩阵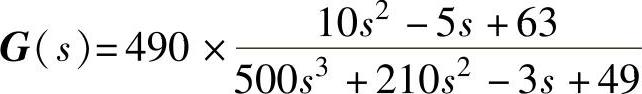 。
。
2)计算原系统的单位阶跃响应。
clear;A=[-0.40-0.01;100;-1.49.8-0.02];B=[6.3;0;9.8];C=[001];D=0;
sys=ss(A,B,C,D);t=0:0.1:120;step(sys,t),grid;
程序运行后绘制单位阶跃响应,如图14-10所示,这是一条发散振荡曲线,系统不能工作。还可调用自编函数tran01.m解算原系统的传递函数矩阵G(s),与可控标准型系统的一样。
3)绘制可控标准型系统仿真模型,如图14-11所示,并对其进行单位阶跃响应仿真。
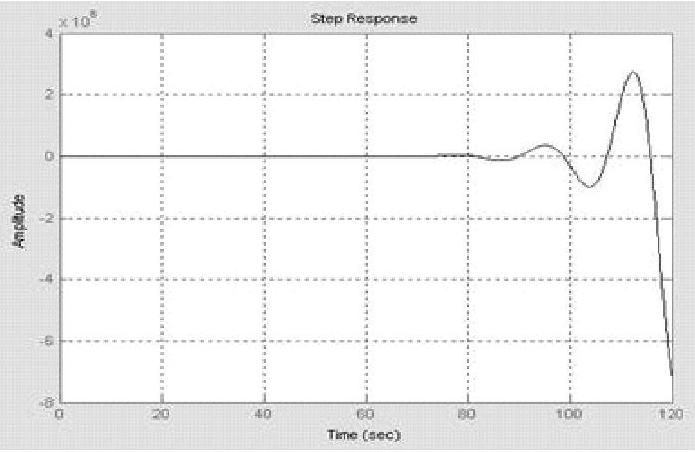
图14-10 原系统单位阶跃响应曲线
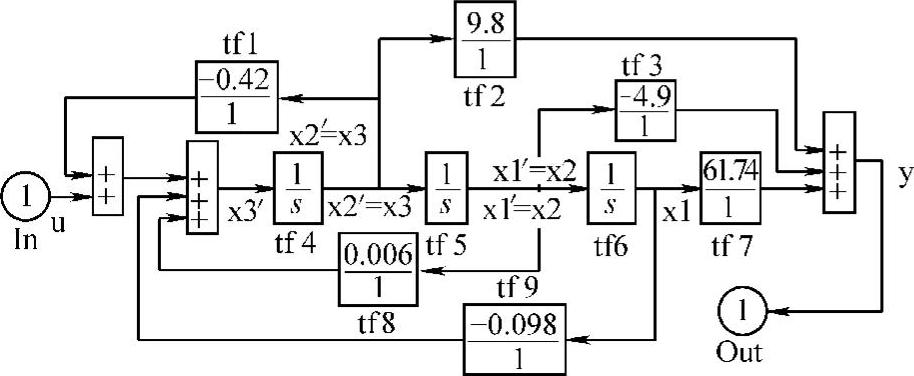
图14-11 系统可控标准型仿真模型sx2L1429.mdl
用系统可控标准型仿真模型仿真绘制单位阶跃响应曲线。
clear;[A,B,C,D]=linmod2( sx2L1429
sx2L1429 );
);
sys=ss(A,B,C,D);t=0:0.1:120;step(sys,t),grid;
程序运行后得到系统可控标准型模型单位阶跃响应曲线仍如图14-10所示,与原系统的单位阶跃响应曲线完全一样。
4)给出以下调用自编函数stabak.m的程序解算系统状态观测器的增益矩阵K。
clear;A=[010;001;-0.09800.0060-0.4200];
B=[0;0;1];C=[61.74-4.99.8];D=0;P=[-2-1+j-1-j];
key=1;[K]=stabak(key,A,B,C,D,P);
程序运行后表明,系统是可控的,系统可实现按题意要求的闭环极点配置;计算得的估计系统状态观测器的增益矩阵为K=[3.90206.0063.58]。
5)绘制带状态反馈增益矩阵K的可控标准型系统仿真模型,如图14-12所示,并对其进行单位阶跃响应仿真。
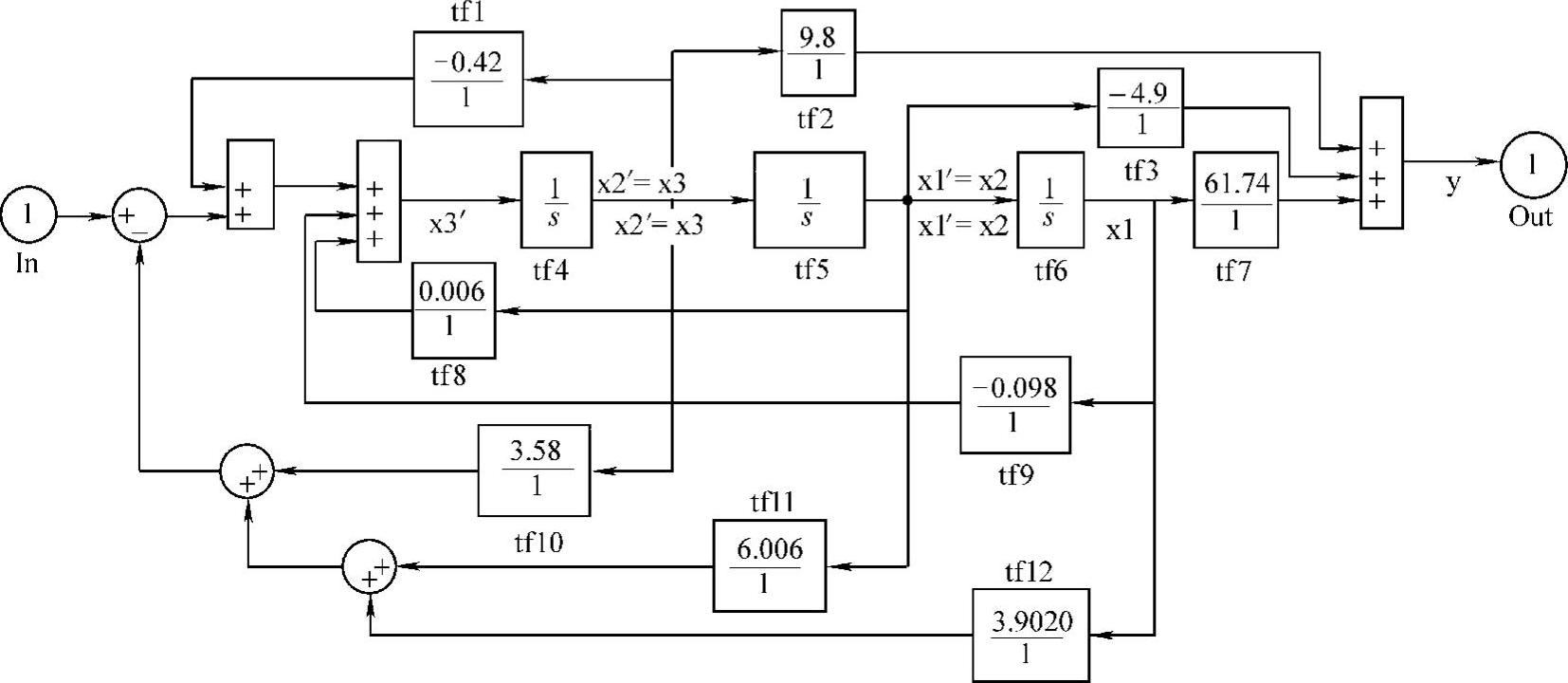
图14-12 带状态反馈增益矩阵K的可控标准型系统仿真模型sx2L1429a.mdl
用系统仿真模型sx2L1429a.m绘制单位阶跃响应曲线。
clear;[A,B,C,D]=linmod2( sx2L1429a
sx2L1429a );
);
sys=ss(A,B,C,D);step(sys),grid;
[y,t]=step(sys);perf(2,y,t);
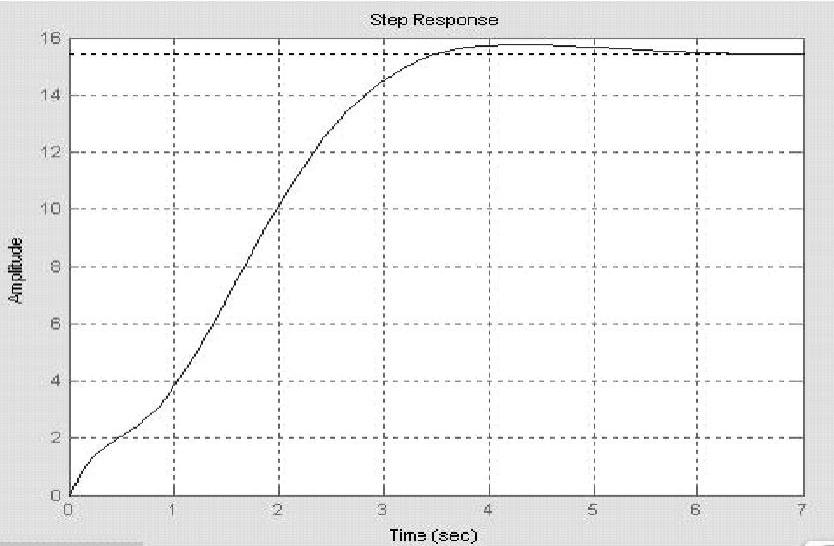
程序运行后得到可控标准型模型带状态反馈增益矩阵K后的系统单位阶跃响应曲线,如图14-13所示,说明系统不仅稳定,而且性能指标优良,σ%=2.2893%。
 (https://www.xing528.com)
(https://www.xing528.com)
图14-13 模型sx2L1429a.mdl的单位阶跃响应曲线
6)给出以下调用自编函数staest.m的程序解算系统的可观性并设计状态观测器。
clear;A=[010;001;-0.09800.0060-0.4200];
B=[0;0;1];C=[61.74-4.99.8];D=0;
P=[-2-1+j-1-j];[CO]=contro(A,B,C,D);
[K,H,AHC]=staest(A,B,C,D,P);
计算结果表明,系统既可控也可观,所以存在状态观测器。系统的状态观测器为

7)绘制带状态反馈增益矩阵K与状态观测器的系统模型sx2L1429b.mdl,如图14-14所示,并仿真。
用带状态反馈增益矩阵K与状态观测器的系统模型sx2L1429b.mdl绘制单位阶跃响应。clear;[A,B,C,D]=linmod2( sx2L1429b
sx2L1429b );sys=ss(A,B,C,D);step(sys),grid;[y,t]=step(sys);perf(2,y,t);
);sys=ss(A,B,C,D);step(sys),grid;[y,t]=step(sys);perf(2,y,t);
程序运行后得到带状态反馈增益矩阵K与状态观测器的系统单位阶跃响应曲线与图14-13相差无几,说明系统不仅稳定,而且性能指标优良,σ%=2.2197%。
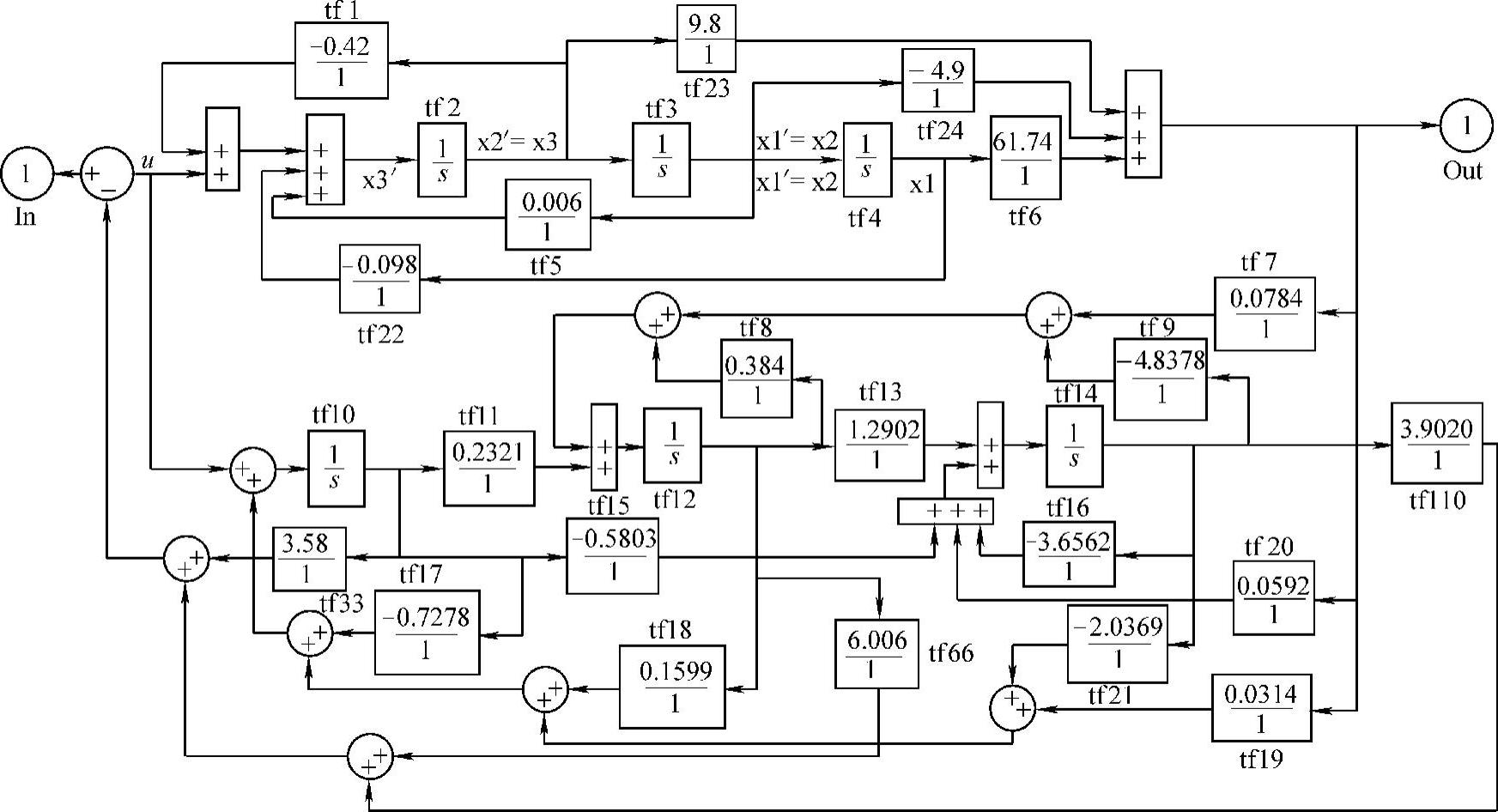
图14-14 带状态观测器与状态观测器的状态反馈增益矩阵K的系统模型sx2L1429b.mdl
8)设计降维状态观测器。
①选择任意矩阵D构造非奇异线性变换矩阵Q:

②根据系统参数,设输出反馈矩阵H ,并用以下MATLAB程序计
,并用以下MATLAB程序计
算det[sE-(A11-HA21)],式中包含输出反馈矩阵元素h1与h2。
clear;syms h1 h2 s;
A1=[010;001;-0.0980.006-0.42];B1=[0;0;1];
C1=[61.74-4.99.8];H=[h1 h2]. ;n=length(A1);E=eye(n-1);
;n=length(A1);E=eye(n-1);
Q=[100;010;61.74-4.99.8];Q1=inv(Q);A=Q∗A1∗Q1;A11=[A(1:2,1:2)];
A21=[A(3,1:2)];eq=collect(det(s∗E-(A11-H∗A21)),s);eqq=vpa(eq,4),
程序运行后得到
eqq=s^2+(55.84∗h1-.5000+57.29∗h2)∗s-388.9∗h1+6.300+55.84∗h2
③根据系统降维观测器的极点满足特征方程λE-(A11-HA21)=0,即
det[sE-(A11-HA21)]=(s+3-j3)(s+3+j3)=s2+6s+18,运行以下语句
clear;syms s;
r=expand((s+3-3∗j)∗(s+3+3∗j)),
语句运行后得到
r=s^2+6∗s+18
④对比以上两式的右端,即可用以下MATLAB语句求出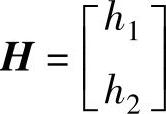 :
:
clear;syms h1 h2;
[h1,h2]=solve( 55.84∗h1-.5+57.29∗h2=6
55.84∗h1-.5+57.29∗h2=6 ,
, -388.9∗h1+6.3+55.84∗h2=18
-388.9∗h1+6.3+55.84∗h2=18 ,
, h1,h2
h1,h2 );
);
h11=vpa(h1,4),h21=vpa(h2,4),
程序运行后得到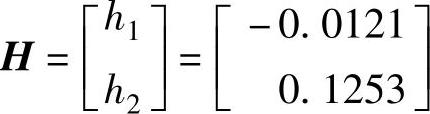 。
。
⑤给出以下调用自编函数reduest.m的程序解算系统可观性并设计降维状态观测器。
clear;A1=[010;001;-0.0980.006-0.42];B1=[0;0;1];
C1=[61.74-4.99.8];D1=0;
Q=[100;010;61.74-4.99.8];;H=[-0.01210.1253]. ;
;
[AHAW,BHBU,AHAY]=reduest(A1,B1,C1,D1,Q,H);
程序运行后得到降维状态观测器动态方程为
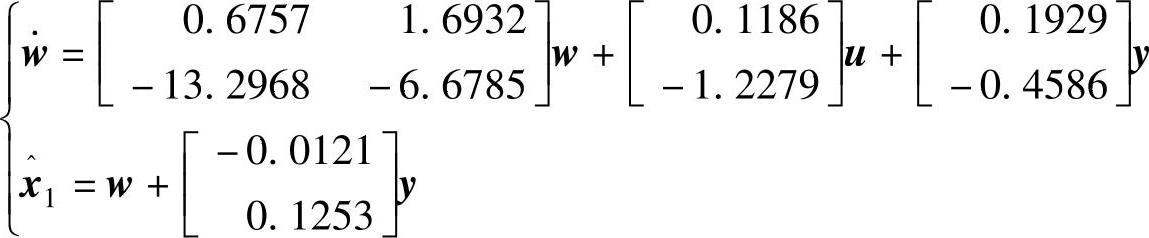
⑥将 变换回到
变换回到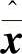 状态空间,计算
状态空间,计算 。
。 、
、 、
、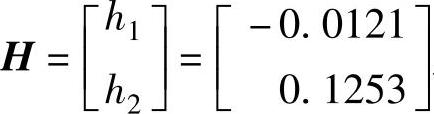 用程序计算。
用程序计算。
clear;Q=[100;010;61.74-4.99.8];
n=size(Q,1);E=eye(n-1);R=inv(Q)∗[E;00],
H=[-0.0121;0.1253];S=inv(Q)∗[H;1],
程序运行后得到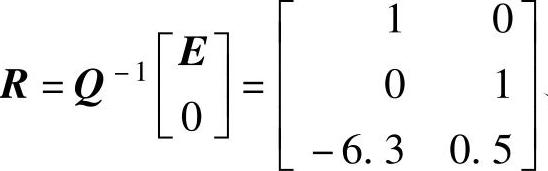 、
、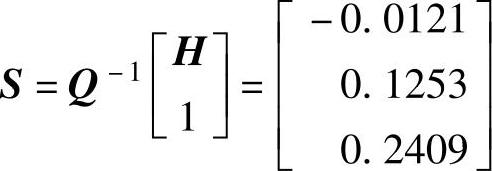 ,那么
,那么

9)绘制带状态反馈增益矩阵K与其降维状态观测器的系统模型sx2L1429c.mdl,如图14-15所示,并对其进行仿真。
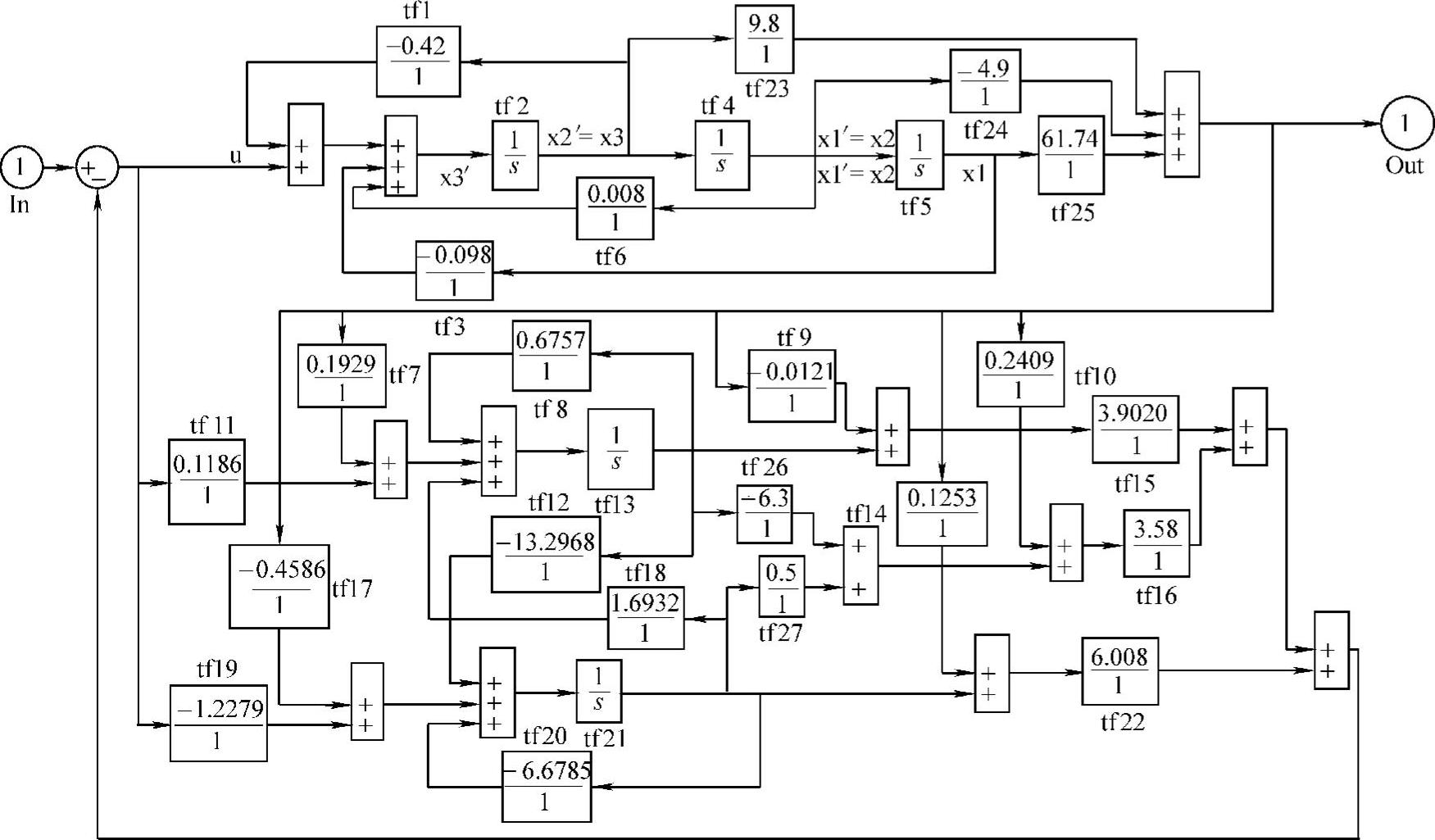
图14-15 带降维状态观测器与其状态反馈增益矩阵K的系统模型sx2L1429c.mdl
用带状态反馈增益矩阵K与其降维状态观测器的系统模型sx2L1429c.mdl绘制单位阶跃响应曲线。
clear;[A,B,C,D]=linmod2( sx2L1429c
sx2L1429c );sys=ss(A,B,C,D);
);sys=ss(A,B,C,D);
step(sys),grid;[y,t]=step(sys);perf(2,y,t);
程序运行后得到带降维状态观测器与其状态反馈增益矩阵K的系统单位阶跃响应曲线与图14-13也相差无几。说明系统不仅稳定,而且性能指标优良,σ%=1.9287%。
本题运算说明:①基于状态空间模型的极点配置不需要附加校正装置,是改变系统性能指标简单可行的重要技术措施。②全维状态观测器与降维状态观测器对系统的响应不起什么作用,其主要功能是观测。③系统模型sx2L1429a.mdl、sx2L1429b.mdl、sx2L1429c.mdl三者阶跃响应曲线的特征、形状都与图14-13基本相同,响应指标数据也非常接近,都使原发散振荡的不稳定系统变成性能指标优良的稳定系统。④用模型图绘制阶跃响应曲线的程序特别简单方便。
【例14-30】 已知系统动态方程的矩阵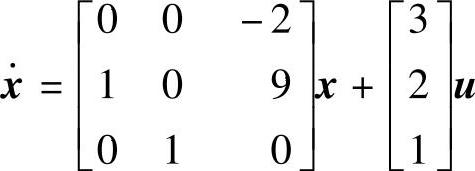 、y=[0 0 1]x。对系统设计降维状态观测器,使得系统的闭环极点为λ1=-3、λ2=-4。
、y=[0 0 1]x。对系统设计降维状态观测器,使得系统的闭环极点为λ1=-3、λ2=-4。
解:1)选择任意矩阵D构造非奇异线性变换矩阵Q:
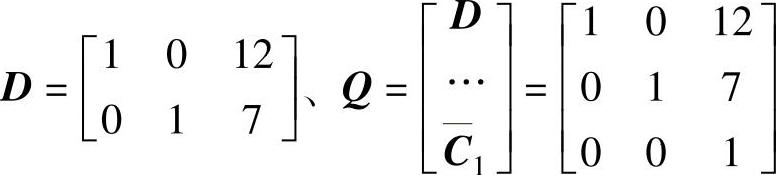
2)根据系统参数,设输出反馈矩阵 ,并用以下MATLAB程序
,并用以下MATLAB程序
计算det[sE-(A11-HA21)]。
clear;syms h1 h2 s;
A1=[00-2;109;010];B1=[3;2;1];C1=[001];
p=[-3-4];E=[10;01];H=[h1 h2]. ;Q=[1012;017;001];
;Q=[1012;017;001];
Q1=inv(Q);A=Q∗A1∗Q1;A11=[A(1:2,1:2)];A21=[A(3,1:2)];
eq=collect(det(s∗E-(A11-H∗A21)),s),
程序运行后得到eq=s^2+(-7+h2)∗s-12+h1,即
det[sE-(A11-HA21)]=s2+(-7+h2)s+(h1-12)
根据自动控制原理公式 有
有

对比上式的两端,即可用以下MATLAB语句求出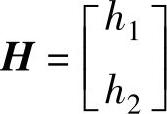 。
。
clear;syms h1 h2;
[h1,h2]=solve( -7+h2=7
-7+h2=7 ,
, h1-12=12
h1-12=12 ,
, h1,h2
h1,h2 ),
),
程序运行后得到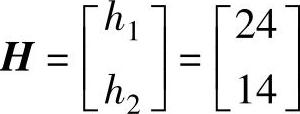 。
。
3)给出以下调用自编函数reduest.m的程序解算系统的可观性并设计降维状态观测器。
clear;A1=[00-2;109;010];B1=[3;2;1];C1=[001];D1=0;
Q=[1012;017;001];H=[24;14];
[AHAW,BHBU,AHAY]=reduest(A1,B1,C1,D1,Q,H);
程序运行后得到降维状态观测器动态方程为
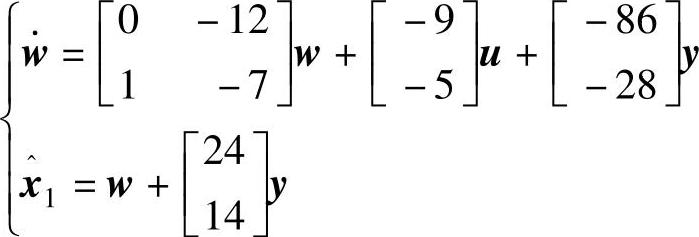
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




