实现系统状态观测器的14.4.2系统

可以证明，当系统完全可观测时，一定存在状态观测器。

MATLAB系统提供了函数acker.m来计算估计器增益矩阵K，使采用全反馈u=-Kx的单输入系统具有指定的闭环极点p。函数命令acker.m的调用格式为

K=acker（A，C，p）

其中输入参数A为系统的状态矩阵，A′是A的转置矩阵；C为系统的观测矩阵，C′是C的转置矩阵；p为指定的闭环系统极点。返回参数K为估计器增益矩阵，而K′=H。

对于已知的实际控制系统{A，B，C}，通过函数命令acker.m先求出K后，进而求得H（K′=H），最后解得状态观测器表达式。

为方便计算，作者编制了判别系统的可观性并设计状态反馈控制器增益矩阵K的函数staest.m。

【例14-27】 续【例14-25】，对1）系统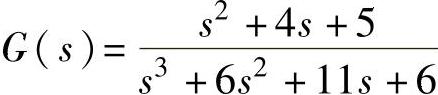，要求闭环极点为λ₁=-2、λ_2.3=-2±j2；2）系统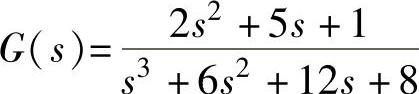，要求闭环极点为λ₁=-0.25、λ_2.3=-1±j。试计算极点配置前后系统的单位阶跃响应；再绘制带状态反馈增益矩阵K的系统状态模型图，并验证配置极点后的单位阶跃响应性能指标。

解：1）已经算出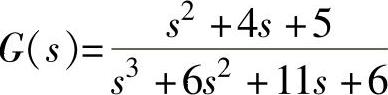的动态方程。

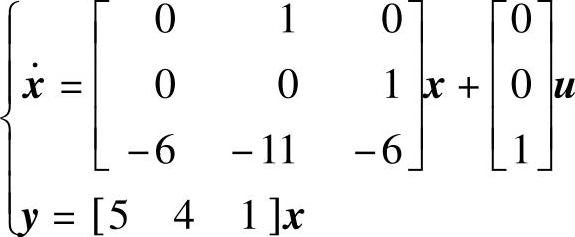①用程序绘制没有配置极点的原系统单位阶跃响应。

clear；A=[0，1，0；0，0，1；-6，-11，-6]；B=[0；0；1]；C=[5，4，1]；D=0；

sys=ss（A，B，C，D）；step（sys），grid；

程序运行后得到原系统1单位阶跃响应曲线如图14-3所示。

②用程序绘制配置极点后系统单位阶跃响应。

clear；A=[0，1，0；0，0，1；-6，-11，-6]；B=[0；0；1]；C=[5，4，1]；D=0；

P=[-2，-2+2∗j，-2-2∗j]；K=place（A，B，P），At=A-B∗K；Bt=B；Ct=C；Dt=D；

sys=ss（At，Bt，Ct，Dt）；step（sys），grid；[y，t]=step（sys）；perf（2，y，t）；

③结论。配置极点前原系统单位阶跃响应曲线虽不超调，但是响应速度很慢，启动时间很长。配置极点后系统阶跃响应曲线如图14-4所示，虽有6.3853%的微超调，但是阶跃响应曲线上升陡，响应速度快很多，配置极点后系统的峰值时间t_p=0.9537s、调节时间t_s=1.5365s。程序运行后还算得反馈增益矩阵K=[1050]。

④绘制带反馈增益矩阵K的系统模型（见图14-5），并用程序验证配置极点后响应性能指标。

clear；[A，B，C，D]=linmod2（sx2L1427）；

sys=ss（A，B，C，D）；step（sys），grid；[y，t]=step（sys）；perf（2，y，t）；

程序运行后得到与图14-4完全相同的结果，既证明带状态反馈增益矩阵的系统状态模型图绘制正确，同时证明以上计算也是正确的。

图14-3 原系统1单位阶跃响应曲线

图14-4 配置极点后系统1单位阶跃响应曲线

图14-5 带反馈增益矩阵K系统1的系统模型sx2L1427.mdl

2）已经算出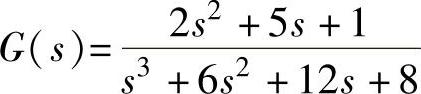的动态方程。

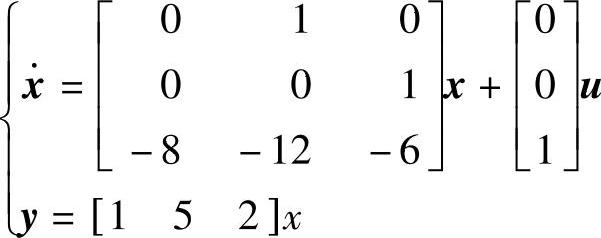①用程序绘制没有配置极点的原系统单位阶跃响应。(www.xing528.com)

clear；A=[0，1，0；0，0，1；-8，-12，-6]；B=[0；0；1]；C=[1，5，2]；D=0；

sys=ss（A，B，C，D）；step（sys），grid；

程序运行后得到原系统2单位阶跃响应曲线如图14-6所示。

②用程序绘制配置极点后系统单位阶跃响应。

clear；A=[010；001；-8-12-6]；B=[0；0；1]；C=[152]；D=0；

P=[-0.25-1+j-1-j]；K=place（A，B，P），At=A-B∗K；Bt=B；Ct=C；Dt=D；

sys=ss（At，Bt，Ct，Dt）；step（sys），grid；[y，t]=step（sys）；perf（2，y，t）；

③结论。配置极点前原系统单位阶跃响应曲线超调很厉害。配置极点后系统单位阶跃响应曲线如图14-7所示，仅有14.9186%的超调，阶跃响应曲线上升也很陡，响应速度不慢，配置极点后系统的峰值时间t_p=2.5432s、调节时间t_s=7.2057s。程序运行后还算得反馈增益矩阵K=[-7.5 -9.5 -3.75]。

图14-6 原系统2单位阶跃响应曲线

图14-7 配置极点后系统2阶跃响应曲线

④绘制带反馈增益矩阵K的系统模型（见图14-8），并用程序验证配置极点后响应性能指标。

clear；[A，B，C，D]=linmod2（sx2L1427a）；

sys=ss（A，B，C，D）；step（sys），grid；[y，t]=step（sys）；perf（2，y，t）；

程序运行后得到与图14-7完全相同的结果，既证明带状态反馈增益矩阵的系统状态模型图绘制正确，同样证明以上计算也是正确的。

图14-8 带反馈增益矩阵K系统2的系统模型sx2L1427a.mdl

【例14-28】 判别以下系统可控、可观性并设计状态观测器。1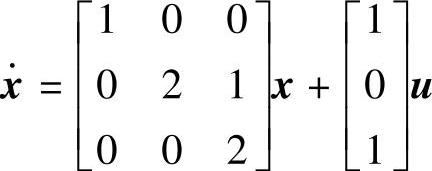）、y=[1 1 0]x，要求闭环极点λ₁=-3、λ₂=-4、λ₃=-5；2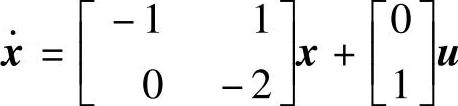）、y=[20]x，要求闭环极点为λ₁=-10、λ₂=-10。

解：1）给出调用自编函数staest.m的程序求解。

clear；A=[100；021；002]；B=[1；0；1]；C=[110]；D=0；P=[-3-4-5]；

[CO]=contro（A，B，C，D）；[K，H，AHC]=staest（A，B，C，D，P）；

程序运行后结果表明系统是可控的也是可观的。还算得全维状态观测器增益矩阵为K=[120-103210]，全维状态观测器的动态方程为

2）也给出调用自编函数staest.m的程序求解。

clear；A=[-11；0-2]；B=[0；1]；C=[20]；D=0；P=[-10-10]；

[CO]=contro（A，B，C，D）；[K，H，AHC]=staest（A，B，C，D，P）；

程序运行后表明系统是可控的也是可观的。程序计算得到全维状态观测器增益矩阵为K=[8.532]，全维状态观测器的动态方程为