如何配置14.4.1系统的极点？

所谓系统的极点配置问题，就是给定了闭环系统的极点位置后，如何通过某种方法来达到给定的极点配置。

对一个可控系统，通过状态反馈的方法，使闭环系统的极点位于预先规定的位置上。由自动控制原理，实现闭环极点任意配置必要且充分条件是系统完全可控。

在MATLAB系统中提供的place（）函数，由指定的闭环系统极点计算状态反馈增益矩阵K。函数的调用格式为

K=place（A，B，p）

其中，输入参数A为系统的状态矩阵，B为系统的输入矩阵，p为指定的闭环系统极点。返回参数K为反馈增益矩阵，即状态反馈矩阵。

函数命令place（）也可计算估计系统状态的装置即观测器的增益矩阵K，使采用全反馈u=-Kx的多输入系统具有指定的闭环极点p。其调用格式为

K=place（A，C，p）

其中，输入参数A为系统状态矩阵，A′是A的转置矩阵；C为系统观测矩阵，C′是C的转置矩阵；p为指定的闭环系统极点。返回参数K为估计系统状态观测器的增益矩阵。

为方便计算，作者编制了判别系统的可控性并设计状态反馈控制器增益矩阵K的函数stabak.m。

【例14-26】 试判别以下系统的可控性并设计状态反馈控制器。已知系统的动态方程为1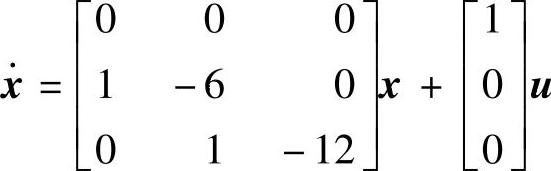），要求系统闭环极点为λ₁=-2、λ_2.3=-1±j；2）x·=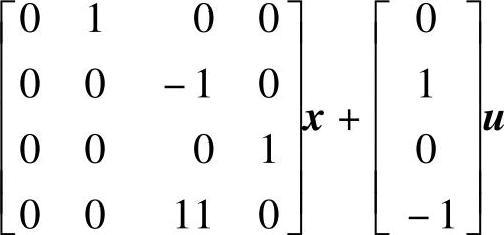、y=[1000]x，要求闭环极点为λ₁=-1、λ₂=-2、λ3.4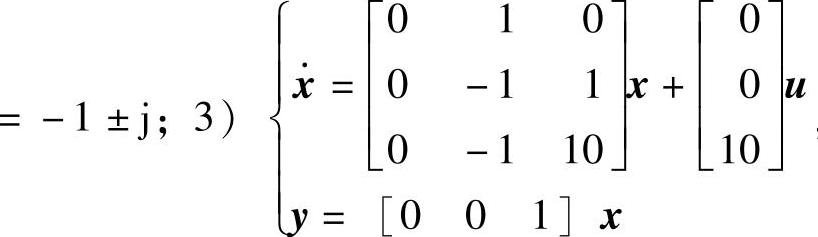，闭环极点为λ₁=-10、λ_2.3=-1±j。

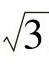解：1）给出调用自编函数stabak.m的程序求解。

clear；A=[000；1-60；01-12]；B=[1；0；0]；C=0；D=0；

P=[-2-1+1i-1-1i]；

key=1；[K]=stabak（key，A，B，C，D，P）；(www.xing528.com)

程序运行后表明，系统是可控的，系统可实现按题意要求的闭环极点配置；计算得的估计系统状态观测器的增益矩阵为K=[-14186-1220]。

2）也给出调用自编函数stabak.m的程序求解。

clear；A=[0100；00-10；0001；00110]；

B=[0；1；0；-1]；C=[1000]；D=0；

p=[-1-2-1+1i-1-1i]；key=1；

[K]=stabak（key，A，B，C，D，p）；

程序运行后表明，系统是可控的，系统可实现按题意要求的闭环极点配置；计算得的估计系统状态观测器的增益矩阵为K=[-0.4-1-21.4-6]。

3）再给出调用自编函数stabak.m的程序求解。

clear；A=[010；0-11；0-110]；

B=[0；0；10]；C=[001]；D=0；

P=[-10-1+sqrt（3）∗j-1-sqrt（3）∗j]；

key=1；[K]=stabak（key，A，B，C，D，P）；

程序运行后表明，系统是可控的，系统可实现按题意要求的闭环极点配置；计算得的估计系统状态观测器的增益矩阵为K=[41.22.1]。