1.线性离散系统的完全可观性
认真复习并理解系统完全可观测的概念。
系统完全可观测的条件为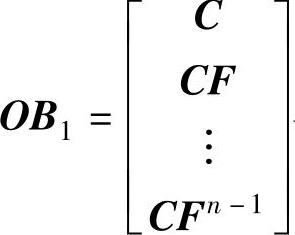 与rank(OB1)=n。可以用MATLAB的求可观性矩阵函数obsv()来计算矩阵OB。函数obsv()的调用格式为
与rank(OB1)=n。可以用MATLAB的求可观性矩阵函数obsv()来计算矩阵OB。函数obsv()的调用格式为
OB=obsv(A,C)
其中,输入参数A即为离散系统的系统矩阵F或者连续系统的系统矩阵A,输入参数C即为离散系统的观测矩阵或者连续系统的观测矩阵,函数返回的就是系统可观性矩阵OB。可见函数obsv()既适用于离散系统,也适用于连续系统。
为方便计算,作者编制了调用系统函数obsv.m确定系统完全可观测性的函数obser.m。请看示例。
【例14-21】 已知离散系统方程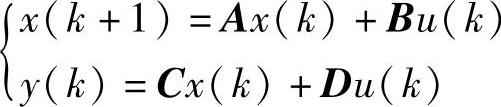 ,式中矩阵
,式中矩阵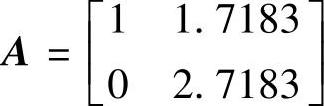 、
、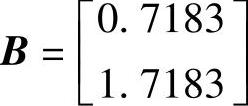 、C=[11]、D=0。1)试用自编函数contro.m判断系统可控性;2)试用自
、C=[11]、D=0。1)试用自编函数contro.m判断系统可控性;2)试用自
编函数obser.m判断系统可观性。
解:给出以下调用自编函数contro.m与obser.m的程序求解。
clear;A=[11.7183;02.7183];
B=[0.7183;1.7183];C=[11];D=0;
[CO]=contro(A,B,C,D);
[OB]=obser(A,B,C,D);
计算结果表明系统既是可控的也是可观的。
2.连续系统的完全可观性
【例14-22】 试判别以下线性系统的可控性及可观(测)性。系统动态方程为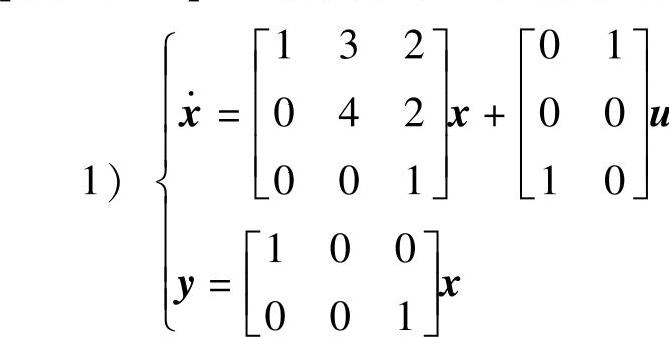 ;2)
;2)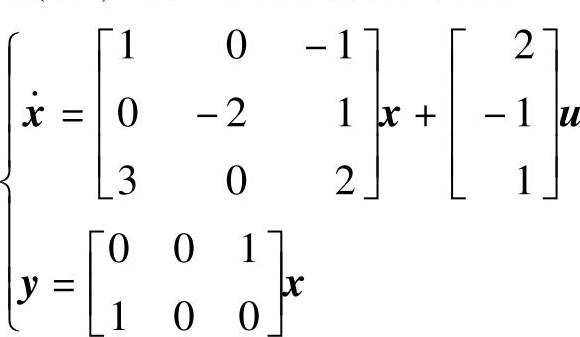 。
。
解:1)给出以下调用自编函数contro.m与obser.m的程序求解。
clear;A=[132;042;001];B=[01;00;10];C=[100;001];D=[0];
[CO]=contro(A,B,C,D);
[OB]=obser(A,B,C,D);
程序运行结果表明,本系统既可控也可观。
2)再给出以下调用自编函数contro.m与obser.m的程序求解。
clear;A=[10-1;0-21;302];B=[2;-1;1];C=[001;100];D=[0];
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
计算结果表明系统是可控但是不可观的。
3.连续系统的完全可观标准型
对于单输出系统{A,B,c,d},若其状态矩阵与输出矩阵有如下的标准形式
则该系统一定可观测,而矩阵对(A,c)被叫做可观标准型。
为方便计算,作者编制了函数obssta.m确定系统可观标准型。
【例14-23】 试对以下系统判断其可观性,再将系统动态方程化为可观标准型并求其变换矩阵。系统动态方程为
解:1)给出以下调用自编函数contro.m、obser.m与obssta.m的程序求解。
clear;A=[-22-1;0-22;1-40];B=[0;1;0];C=[011];D=[0];
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
[M,A1,B1,C1]=obssta(A,B,C,D);
程序运行后得到转换前系统可控也可观,转换后系统也可观,带可观标准型的动态方程为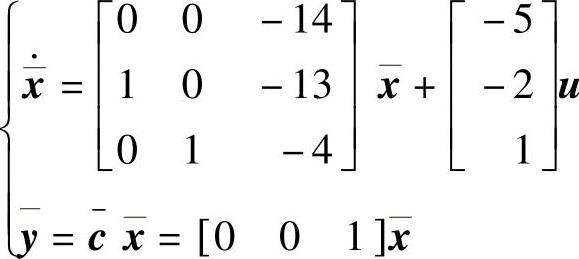 ,变换矩阵为
,变换矩阵为 。
。
2)也给出以下调用自编函数contro.m、obser.m与obssta.m的程序求解。
clear;A=[2-1-1;0-10;021];B=[7;2;1];C=[110];D=[0];
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
[M,A1,B1,C1]=obssta(A,B,C,D);
程序运行后得到转换前系统可控也可观,转换后系统也可观,带可观标准型的动态方程为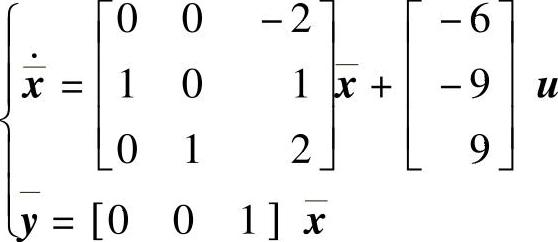 ,变换矩阵为
,变换矩阵为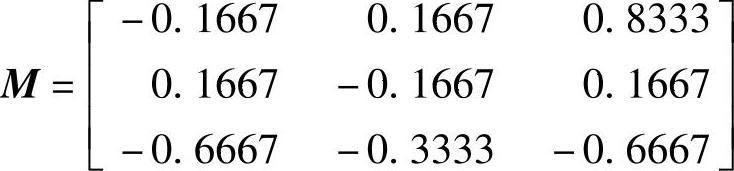 。(https://www.xing528.com)
。(https://www.xing528.com)
3)还给出以下调用自编函数contro.m、obser.m与obssta.m的程序求解。
clear;A=[32;1-1];B=[1;2];C=[11];D=[0];
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
[M,A1,B1,C1]=obssta(A,B,C,D);
程序运行后得到转换前系统可控也可观,转换后系统也可观,带可观标准型的动态方程为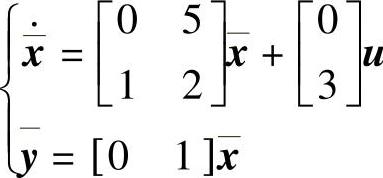 ,变换矩阵为
,变换矩阵为 。
。
4)再给出以下调用自编函数contro.m、obser.m与obssta.m的程序求解。
clear;A=[-100;0-20;00-3];B=[2;3;4];C=[1-12];D=[0];
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
[M,A1,B1,C1]=obssta(A,B,C,D);
程序运行后得到转换前系统可控也可观,转换后系统也可观,带可观标准型的动态方程为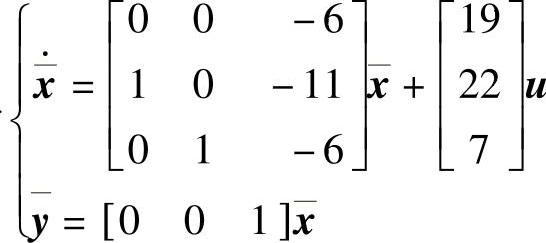 ,变换矩阵为
,变换矩阵为 。
。
【例14-24】 续【例14-2】,试确定图14-2所示系统的可控性与可观性。
解:1)给出调用系统函数linmod2.m与自编函数contro.m、obser.m的程序解算。
clear;[A,B,C,D]=linmod2( sx2L1402a
sx2L1402a ),
),
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
程序运行后得到动态方程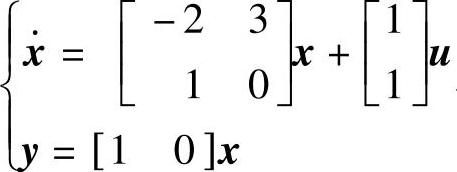 与对应的系统不可控但可观。
与对应的系统不可控但可观。
2)也给出调用系统函数linmod2.m与自编函数contro.m、obser.m的程序解算。
clear;[A,B,C,D]=linmod2( sx2L1402b
sx2L1402b ),
),
[CO]=contro(A,B,C,D);[OB]=obser(A,B,C,D);
程序运行后得到系统动态方程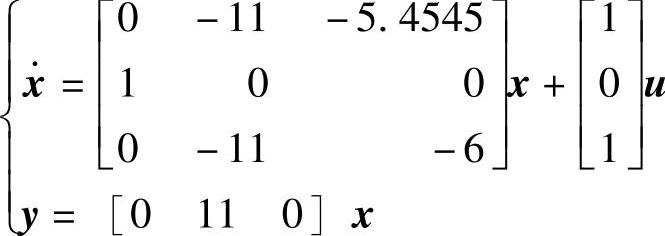 与对应的系统是既可控也可观。
与对应的系统是既可控也可观。
4.线性定常系统的实现问题
线性系统的实现问题是给定系统的传递函数G(s),求系统A、B、C、D阵的问题。
对于SISO线性定常系统,如果其传递函数是可实现的,则有任意维数的动态方程与之对应。其动态方程维数最小的实现称为最小实现,最小实现的维数等于传递函数的阶数。
以下介绍SISO系统可控标准型与可观标准型实现的示例。
【例14-25】 已知系统传递函数1)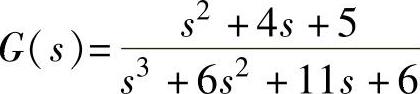 ;2)
;2)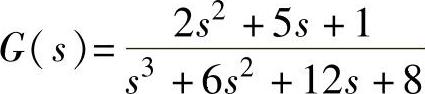 ;3)
;3) ,试求系统可控性及可观性的动态方程实现。
,试求系统可控性及可观性的动态方程实现。
解:1)对第1个系统传递函数,可直接写出系统的可控标准型:
系统的可观标准型为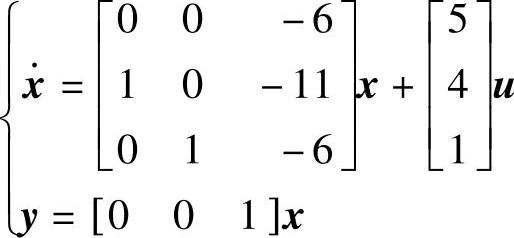
对于可控标准型可用自编函数ssto2.m验证以上计算是否正确。
clear;A=[010;001;-6-11-6];B=[0;0;1];C=[541];D=0;
key=1;G=ssto2(key,A,B,C,D);
对于可观标准型,读者可按可控标准型的程序自行验算。
clear;A=[00-6;10-11;01-6];B=[5;4;1];C=[001];D=0;
key=1;G=ssto2(key,A,B,C,D);
2)对第2个系统传递函数,可直接写出系统的可控标准型:
系统的可观(测)标准型为
读者可自行验证以上计算是否正确。
3)对第3个系统传递函数,可直接写出系统的可控标准型:
系统的可观(测)标准型为
读者可自行验证以上计算是正确的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




