如何创造可控性的线性系统？

系统完全可控的必要且充分的条件是：

可以用MATLAB计算可控性矩阵的函数ctrb（），来求可控性矩阵CO（n×np）。函数命令ctrb（）的调用格式为

CO=ctrb（A，B）

其输入参数A为离散系统的系统矩阵F或者连续系统的系统矩阵A，输入参数B为离散系统的控制矩阵G或者连续系统的控制矩阵B，函数返回的就是系统可控性矩阵CO。函数ctrb（）既适用于离散系统，也适用于连续系统。

为方便计算，作者编制了调用系统命令ctrb.m判定系统能控性的函数contro.m。

1.离散系统的完全可控性示例

【例14-17】 在离散系统方程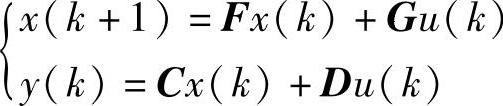中，已知矩阵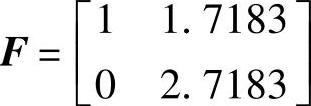、G、C=[1 1]、D=0。试采用自编函数验算rank [G　FG…F^n-1G]=n，并判定离散系统的可控性。

解：给出调用自编函数contro.m的程序求解。

clear；F=[11.7183；02.7183]；A=F；

G=[0.7183；1.7183]；B=G；C=[11]；D=0；

[CO]=contro（A，B，C，D）；

程序运行后得到rank[G　FG…F^n-1G]=n=2，故该离散系统是可控的。

2.连续系统的完全可控性示例

线性系统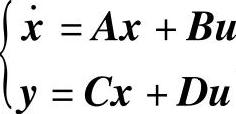完全可控的条件是

【例14-18】 已知状态方程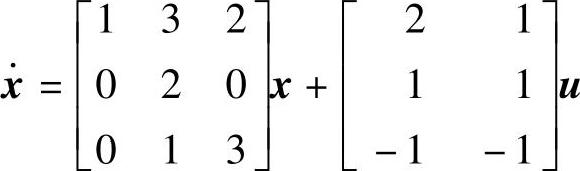，试确定系统的可控性。

解：给出调用自编函数contro.m的程序求解。

clear；A=[132；020；013]；B=[21；11；-1-1]；

C=[00]；D=0；[CO]=contro（A，B，C，D）；程序运行后得到rank[B　AB　A²B…A^n-1B]=2<n=3，故该系统是不可控的。当状态方程为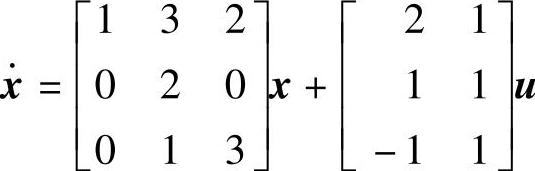时，系统是可控的。请读者自行验证。

3.连续系统的状态完全可控标准型

对于单输入系统{A，b}，若其状态矩阵与输入矩阵具有如下的正则标准形式：

则系统一定可控，该矩阵对（A，b）叫做可控标准型。

为方便计算，作者编制了确定系统可控标准型的函数consta.m。请看示例。

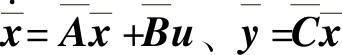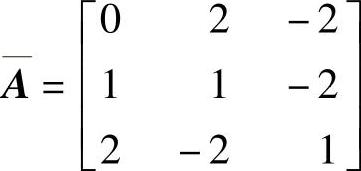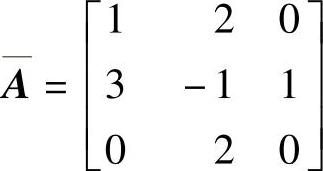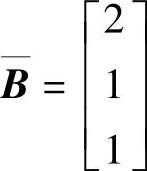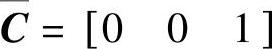【例14-19】 已知系统空间模型，式中矩阵1）、B=、；2）、、；3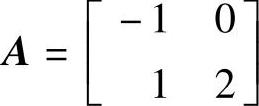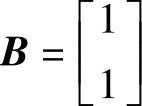）、。试将系统状态方程化为可控标准型并确定原系统与变换后系统是否可控。

解：1）给出调用自编函数consta.m的程序求解。

clear；A1=[02-2；11-2；2-21]；B1=[2；1；1]；

C1=[111]；[P，A，B，C]=consta（A1，B1，C1）；

程序运行后得到系统的可控标准型为

程序运行后还得到原系统与变换后系统都是可控的。

2）也给出调用自编函数consta.m的程序求解。

clear；A1=[120；3-11；020]；B1=[2；1；1]；

C1=[001]；[P，A，B，C]=consta（A1，B1，C1）；

程序运行后得到系统的变换矩阵与可控标准型为

程序运行后还得到原系统与变换后系统都是可控的。

3）还给出调用自编函数consta.m的程序求解。

clear；A1=[-10；12]；B1=[1；1]；C1=[00]；(www.xing528.com)

[P，A，B，C]=consta（A1，B1，C1）；

运行结果得到系统的可控标准型为

程序运行后还得到原系统与变换后系统都是可控的。

4.连续系统的输出可控性

系统输出完全可控的必要充分条件为下列q×（n+1）p维输出可控性矩阵T有

式中，q为输出变量的维数。

为方便计算，作者编制了确定系统输出可控性的函数outcon.m。请看示例。

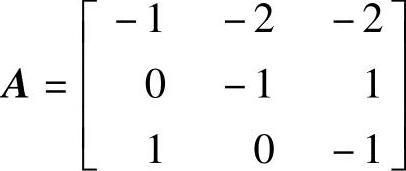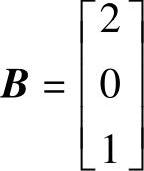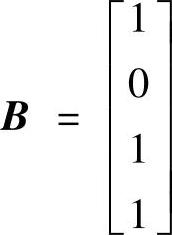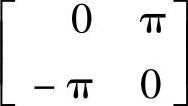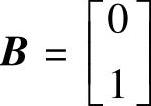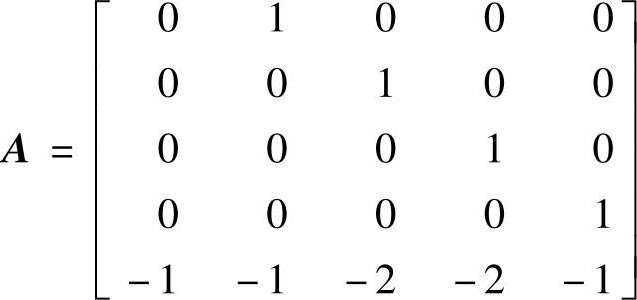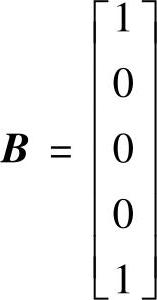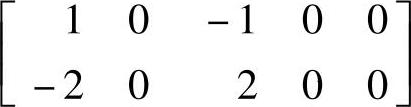【例14-20】 已知控制系统动态方程的3个矩阵为1）、、C=[110]；2）、、C=[1101]；3）A=、、C=[12]；4）、、C=；5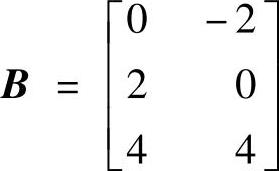）、、C=[001]、D=[1 -1]，试计算输出可控性矩阵T并确定系统状态的可控性与输出可控性。

解：1）给出以下调用自编函数contro.m与outcon.m的程序求解。

clear；A=[-1-2-2；0-11；10-1]；B=[2；0；1]；C=[110]；D=0；

[CO]=contro（A，B，C，D）；[T]=outcon（A，B，C，D）；

运行结果表明，系统是可控的；输出可控性矩阵T=[2-300]，并且系统输出也是可控的。

2）再给出以下调用自编函数contro.m与outcon.m的程序求解。

clear；A=[-4000；0-100；00-20；000-3]；

B=[1；0；1；1]；C=[1101]；D=0；

[CO]=contro（A，B，C，D）；[T]=outcon（A，B，C，D）；

运行结果表明，系统不可控；输出可控性矩阵T=[2-725-910]，而系统输出是可控的。

3）也给出以下调用自编函数contro.m与outcon.m的程序求解。

clear；A=[0 pi；-pi 0]；B=[0；1]；C=[12]；D=0；

[CO]=contro（A，B，C，D）；[T]=outcon（A，B，C，D）；

运行结果表明，系统是可控的；输出可控性矩阵T=[23.14160]，并且系统输出也是可控的。

4）还给出以下调用自编函数contro.m与outcon.m的程序求解。

clear；A=[01000；00100；00010；00001；-1-1-2-2-1]；

B=[1；0；0；0；1]；C=[10-100；-20200]；D=[0；0]；

[CO]=contro（A，B，C，D）；[T]=outcon（A，B，C，D）；

运行结果表明，系统是可控的；输出可控性矩阵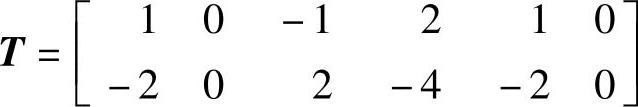，系

统输出是不可控的。

5）给出以下调用自编函数contro.m与outcon.m的程序求解。

clear；A=[010；001；0-2-2]；

B=[0-2；20；44]；C=[001]；D=[1-1]；

[CO]=contro（A，B，C，D）；

[T]=outcon（A，B，C，D）；

已经说明系统可控；程序运行后得到输出可控性矩阵T=[4 4 -12 -8 16 8 1 -1]，系统输出也是可控的。