将状态方程化为约当标准型

如果矩阵A_n×n有相重的特征值，并且按λ_i所解得的独立特征向量的数目小于n，则矩阵A不能化为对角阵。但仍存在一个线性变换矩阵P，使A变换成

J=P^-1AP

J叫做约当（Jordan）标准型矩阵，简称约当标准型。

在MATLAB中用函数命令jordan（）求矩阵的约当标准型。函数的调用格式为

[V，J]=jordan（A）

这种格式函数的输入参数A是对象矩阵，输出参数J是矩阵A的Jordan标准型矩阵，输出参数V即是那个使约当标准型满足J=V\A·V=V^-1·A·V的非奇异矩阵。

为方便计算，作者编制了利用MATLAB系统函数命令jordan.m计算约当标准型的函数jorsta.m。请看示例。

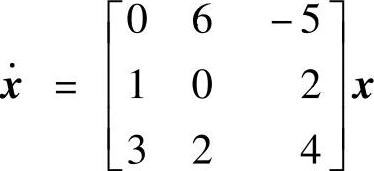【例14-16】 已知系统状态空间表达式1）、y=[100]x；2）、y=[110]x；3）；4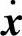）=，试将动态方程式化为约当标准型。

解：1）给出调用自编函数jorsta.m的程序求解。

clear；A=[010；001；230]；B=[0；0；1]；C=[100]；

[V，J，A1，B1，C1]=jorsta（A，B，C）；

程序运行后得到矩阵A的约当标准型，系统线性变换后的方程、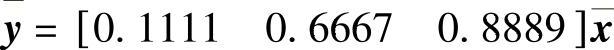，并验证了系统状态矩阵特征值的不变性。

2）同样给出调用自编函数jorsta.m的程序求解。(www.xing528.com)

clear；A=[010；001；-1-3-3]；B=[0；0；1]；C=[110]；

[V，J，A1，B1，C1]=jorsta（A，B，C）；

程序运行后得到矩阵A的约当标准型，系统线性变换后的方程、，并验证了系统状态矩阵特征值的不变性。

3）也给出调用自编函数jorsta.m的程序求解。

clear；A=[06-5；102；324]；B=[0；0；0]；C=[000]；

[V，J，A1，B1，C1]=jorsta（A，B，C）；

程序运行后得到矩阵A的约当标准型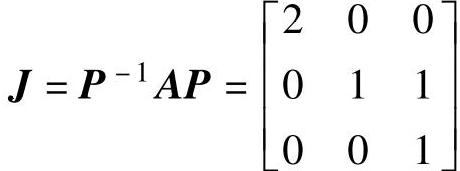，系统线性变换后的方程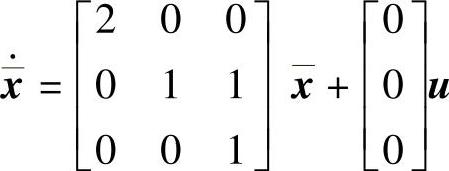、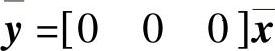，并验证了系统状态矩阵特征值的不变性。

4）还给出调用自编函数jorsta.m的程序求解。

clear；A=[300；241；214]；B=[0；0；0]；C=[000]；

[V，J，A1，B1，C1]=jorsta（A，B，C）；

程序运行后得到矩阵A的约当标准型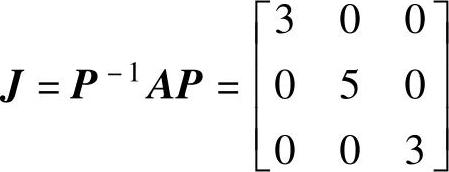，系统线性变换后的方程、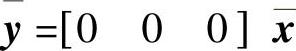，并验证了系统状态矩阵特征值的不变性。