控制系统P-1变换优化策略

从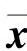坐标系逆向变回到x坐标系，所进行的变换为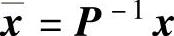，即由（A、B、C）求（A、B、C）。根据自动控制原理，两坐标系相应矩阵之间有以下关系

存在，此则称为对系统进行P^-1变换。已经说明过，同一系统特征值不变。为方便计算，作者编制了对系统进行P^-1变换即从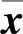坐标系逆向变回到x坐标系的函数lintra02.m。

【例14-11】 对【例14-10】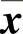坐标系里的系统进行坐标反变换（从坐标系逆向变换到x坐标系）。

解：给出调用自编函数lintra02.m的程序求解。

clear；A1=[-20；3-1]；B1=[1.5；-0.5]；C1=[33]；

P1=[0.50.5；0.5-0.5]；[A，B，C]=lintra02（A1，B1，C1，P1）；

程序运行后得到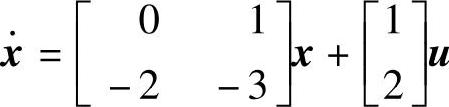、y=[30]x，即为x坐标系里的动态方程。

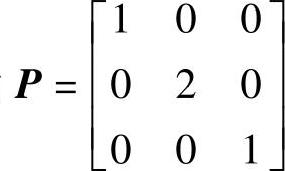【例14-12】 已知控制系统，1）欲对系统进行坐标变换，其变换关系为，试求系统线性变换后的系统动态方程，并验证系统状态矩阵特征值的不变性；2）对坐标系里的系统进行坐标反变换。

解：1）给出调用自编函数lintra01.m的程序求解。(www.xing528.com)

clear；syms s t；A=[-210；0-30；01-4]；B=[-1-1；14；2-3]；

C=[000]；P=[100；020；001]；[A1，B1，C1]=lintra01（A，B，C，P）；

程序运行后得坐标系的系统动态方程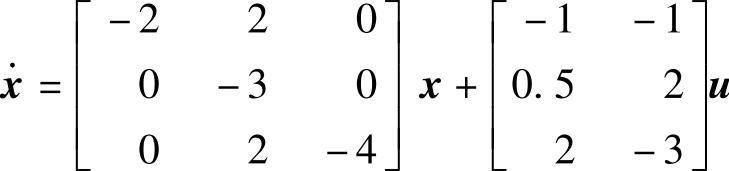，还有变换关系式。

2）给出调用自编函数lintra02.m的程序对x坐标系里的系统进行坐标反变换

clear；A1=[-220；0-30；02-4]；B1=[-1-1；0.52；2-3]；C1=[000]；

P1=[100；00.50；001]；

[A，B，C]=lintra02（A1，B1，C1，P1）；

程序运行后得到x坐标系里的动态方程，还有变换关系式P。