控制系统状态转移矩阵的求解方法

控制系统状态转移矩阵Φ（t）又称为矩阵指数函数。根据幂级数展开式有

式中，E为n阶单位矩阵。

为方便计算，作者编制了求控制系统的状态转移矩阵Φ（t）的函数phi01.m。

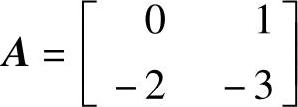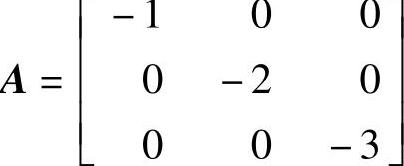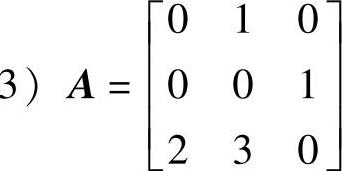【例14-4】 已知以下控制系统状态矩阵为1），2)，，4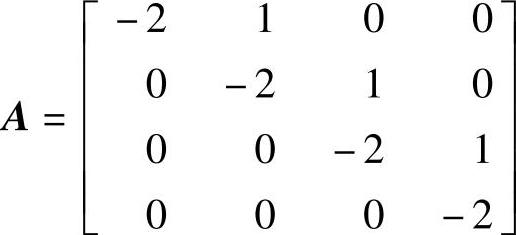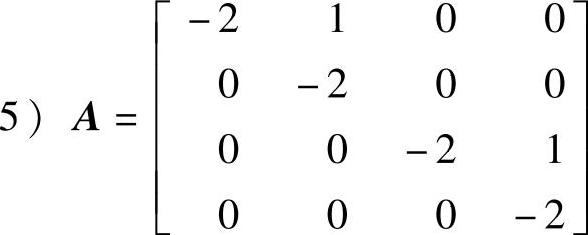），，用自编函数求5个控制系统的状态转移矩阵Φ（t）并验证求解的Φ（t）是否正确。

解：1）对第1个系统给出以下调用自编函数phi01.m的程序解算。

clear；syms s t；A=[01；-2-3]；

[sea，detsea，invsea，phit]=phi01（A）；

程序运行后得到。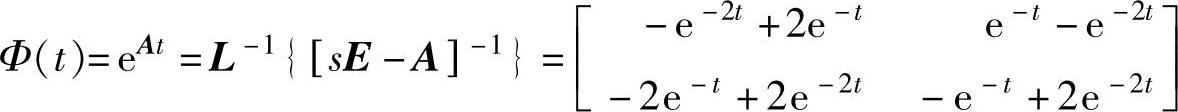

调用自编函数phit01.m的验证程序如下。

clear；t=sym（t）；

phit=[2∗exp（-t）-exp（-2∗t）exp（-t）-exp（-2∗t）；-2∗exp（-t）+2∗exp（-2∗t）-exp（-t）+2

∗exp（-2∗t）]；

[A]=phit01（phit）；

程序运行后计算结果说明求得的Φ（t）正确。

2）对第2个系统也给出以下调用自编函数phi01.m的程序解算。

clear；syms s t；A=[-100；0-20；00-3]；

[sea，detsea，invsea，phit]=phi01（A）；

程序运行后得到。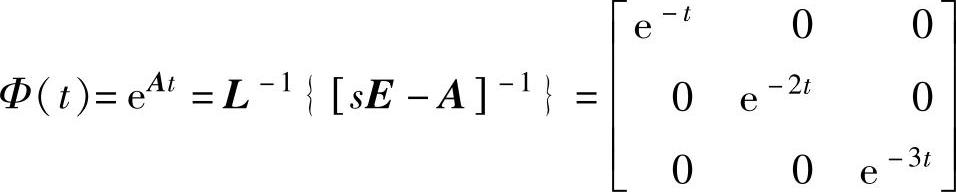

调用自编函数phit01.m的验证程序如下。

clear；t=sym（t）；

phit=[exp（-t）00；0 exp（-2∗t）0；00 exp（-3∗t）]；(www.xing528.com)

[A]=phit01（phit）；

程序运行后计算结果说明求得的Φ（t）正确。

需要特别说明，以下解题无须给出程序，按以上程序改变给定的系统状态矩阵A数据即可，在此给出各题程序运行结果。读者还可以按以上解题加以验证。

3）第3个系统。

4）第4个系统。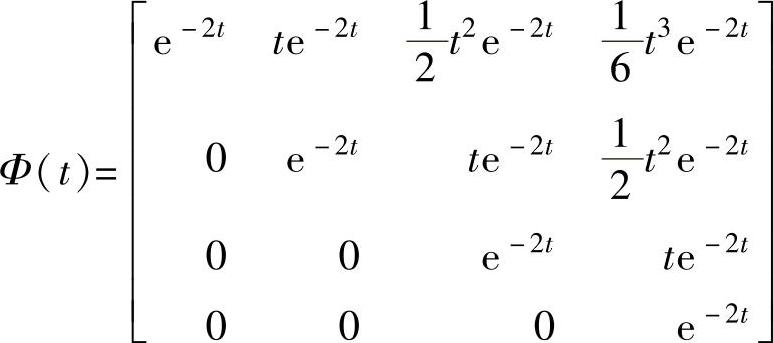

5）第5个系统。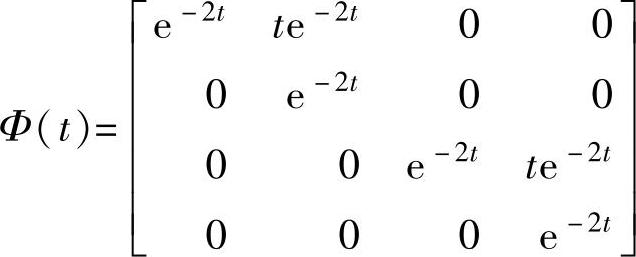

【例14-5】 已知系统状态矩阵为，试求：1）控制系统的特征矩阵；2）特征矩阵的行列式；3）特征矩阵的逆；4）求控制系统的状态转移矩阵Φ（t）。

解：给出以下调用自编函数phi01.m的程序解算，函数phi01.m本身就有计算系统的特征矩阵、特征矩阵行列式与特征矩阵的逆的功能，只不过在【例14-4】中没有要求而已。

clear；syms s t；A=[010；001；2-54]；

[sea，detsea，invsea，phit]=phi01（A）；

程序运行后得到

1）特征矩阵：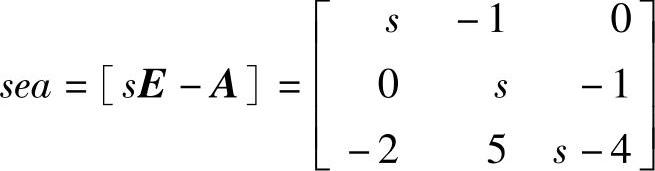

2）特征矩阵的行列式：det sea=|sE-A|=s³-4s²+5s-2=（s-2）（s-1）²

3）特征矩阵的逆：

4）状态转移矩阵：

调用自编函数phit01.m的验证程序如下。

clear；t=sym（t）；

phit=[exp（2∗t）-2∗t∗exp（t），-2∗exp（2∗t）+2∗exp（t）+3∗t∗exp（t），exp（2∗t）-exp（t）-t∗exp（t）；2∗exp（2∗t）-2∗exp（t）-2∗t∗exp（t），-4∗exp（2∗t）+5∗exp（t）+3∗t∗exp（t），2∗exp（2∗t）-2∗exp（t）-t∗exp（t）；4∗exp（2∗t）-4∗exp（t）-2∗t∗exp（t），-8∗exp（2∗t）+8∗exp（t）+3∗t∗exp（t），4∗exp（2∗t）-3∗exp（t）-t∗exp（t）]；

[A]=phit01（phit）；

程序运行后计算结果说明求得的Φ（t）正确。