有三种方法建立控制系统状态空间表达式:一是直接根据控制系统工作原理建立相应的微分方程或差分方程,再将其整理、规范化而得;二是由控制系统结构框图建立系统状态空间表达式;三是由已知系统的某种数学模型转化而得。请看示例。
图14-1 网络电路
【例14-1】 已知图14-1所示系统元件参数,输入为u1(t)与u2(t),输出为y(t),试列写图示网络的状态空间表达式。解:选择电感电流与电容电压作为状态变量,即x1=i1、x2=i2、x3=uc。根据基尔霍夫第一定律、第二定律,有
将状态变量代入并整理得到状态空间表达式
写成矩阵形式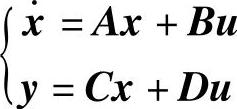
式中 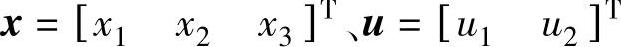
【例14-2】 试求图14-2所示系统的动态方程,并求其对应的传递函数。
图14-2 模型sx2L1402a.mdl和模型sx2L1402b.mdl
解:1)给出调用系统函数linmod2.m与自编函数ssto2.m的程序解算。
clear;[A,B,C,D]=linmod2( sx2L1402a
sx2L1402a ),
),
key=1;G=ssto2(key,A,B,C,D);
程序运行后得到动态方程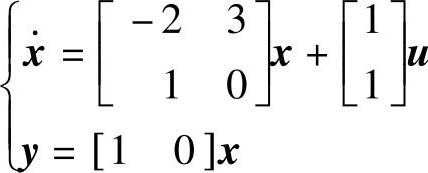 与传递函数
与传递函数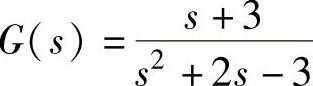 。
。
2)也给出调用系统函数linmod2.m与自编函数ssto2.m的程序解算。
clear;[A,B,C,D]=linmod2( sx2L1402b
sx2L1402b ),
),
key=1;G=ssto2(key,A,B,C,D);
程序运行后得到系统动态方程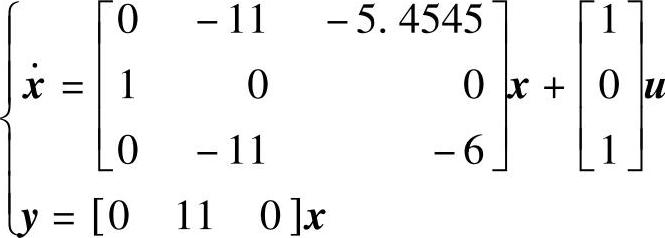 与对应的传递函数
与对应的传递函数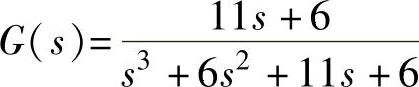 。
。
【例14-3】 已知连续系统零极点增益模型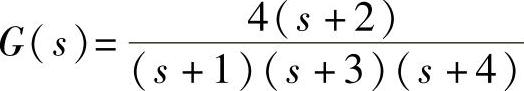 、系统微分方程为
、系统微分方程为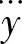
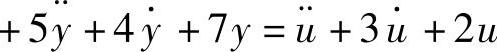 ,求系统的状态空间表达式。
,求系统的状态空间表达式。
解:1)给出以下调用自编函数zpkto2.m的程序实现,并用自编函数ssto2.m的程序来验证。
clear;k=4;z=-2;p=[-1,-3,-4];key=2;
G=zpkto2(key,z,p,k);(https://www.xing528.com)
程序运行后得到系统空间表达式为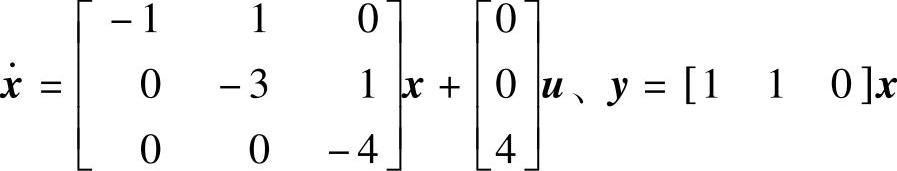 。可用以下程序验证计算是否正确。
。可用以下程序验证计算是否正确。
clear;A=[-110;0-31;00-4];B=[0;0;4];C=[110];
D=0;key=2;G=ssto2(key,A,B,C,D);
2)求系统微分方程为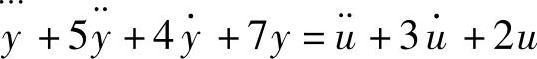 对应的状态空间表达式。此微分方程式含有输入函数导数项,其一般表达式[10]为
对应的状态空间表达式。此微分方程式含有输入函数导数项,其一般表达式[10]为
按参考文献[10]选取系统状态变量并有相关公式
①按式(14-1)~式(14-5)得到a1=5、a2=4、a3=7、b0=0、b1=1、b2=3、b3=2。运行以下程序计算H=[h1;h2;h3]。
clear;a1=5;a2=4;a3=7;b0=0;b1=1;b2=3;b3=2;
h1=b1-a1∗b0,h2=(b2-a2∗b0)-a1∗h1,
h3=(b3-a3∗b0)-a2∗h1-a1∗h2,
程序运行后得到H=[h1;h2;h3]=[1;-2;8]。再选取状态变量x1=y、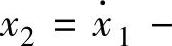
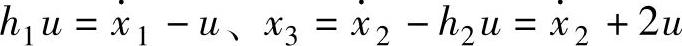 ,则有
,则有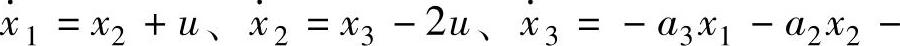 a1x3+8u=-7x1-4x2-5x3+8u。
a1x3+8u=-7x1-4x2-5x3+8u。
由此写出状态方程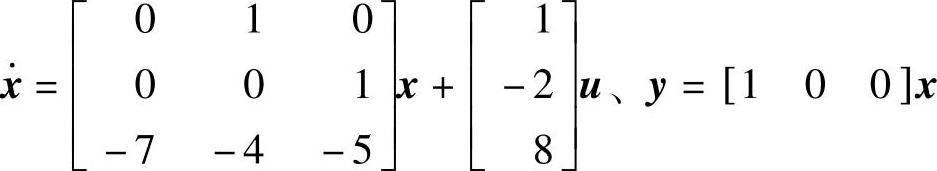 。运行以下程序求传递函数矩阵。
。运行以下程序求传递函数矩阵。
clear;A=[010;001;-7-4-5];B=[1;-2;8];C=[100];
D=0;[invsea,G]=tran01(A,B,C,D);
程序运行后得到微分方程对应的系统传递函数为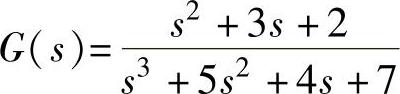 。
。
②按参考文献[12]公式得到a1=5、a2=4、a3=7、b0=0、b1=1、b2=3、b3=2。选取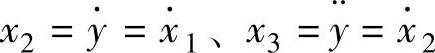 ,那么
,那么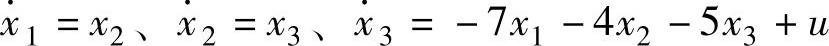 ,则
,则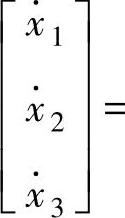
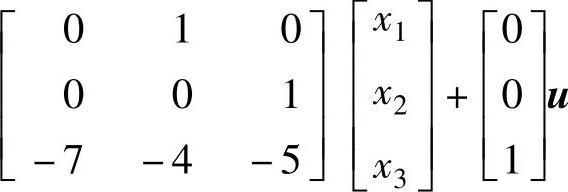
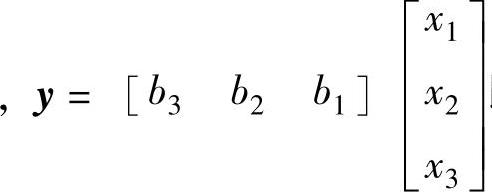 即
即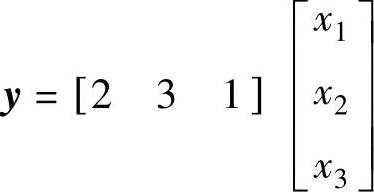
自动控制原理中已经学过,对于一个系统,尽管其状态空间表达式不是唯一的,但其传递函数矩阵不变。可用以下程序验证。
clear;A=[010;001;-7-4-5];B=[0;0;1];C=[231];
D=0;[invsea,G]=tran01(A,B,C,D);
程序运行后得到传递函数矩阵不变,说明以上计算正确。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




