MATLAB计算及仿真：前馈控制系统优化

前馈控制是将扰动信号经前馈控制器处理后用以消除扰动对被调量的影响，它是按扰动进行的补偿控制。不变性原理是实现前馈控制的理论基础。“不变性”是指控制系统的被调量不受扰动作用的影响，与扰动完全无关，或在一定准确度下无关。

前馈控制系统框图如图13-62所示。图中G_f（s）是扰动通道的传递函数，G_M（s）是前馈校正器的传递函数，由图可知C（s）=G_f（s）F（s）+G_M（s）G₀（s）F（s）。根据不变性原理，应有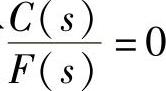，得前馈校正器的模型

为。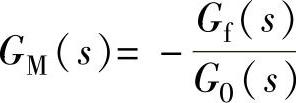

【例13-9】 已知一前馈—反馈复合控制系统如图13-63所示，系统的控制通道特性、扰动通道特性传递函数分别为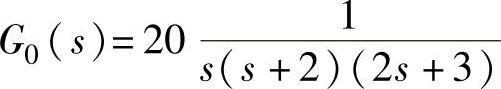；Gf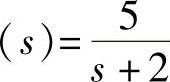。试对系统进行滞后校正，使系统的相角稳定裕度γ≥45°；设计前馈控制系统，使系统能克服扰动对系统的影响。

图13-62 前馈控制系统框图

图13-63 前馈—反馈复合控制系统结构框图

解：1）检查原系统跟随性能指标。

clear；k0=20；n1=[1]；d1=conv（conv（[12]，[23]），[10]）；

s1=tf（k0∗n1，d1）；figure（1）；margin（s1）；pause；

figure（2）；sys=feedback（s1，1）；step（sys），

程序运行后，可得未校正系统Bode图（见图13-64）与频域性能指标，还有如图13-65的未校正系统阶跃响应曲线。由计算数据可知未校正系统频域性能指标：

幅值稳定裕度：L_h=0.424dB -π穿越频率：ω_g=1.73rad/s

相角稳定裕度：γ=1.39° 剪切频率：ω_c=1.69rad/s

图13-64 未校正系统的Bode图

由图13-65可见，未校正系统相角稳定裕度γ=1.39°<45°不满足要求，阶跃响应振荡曲线虽然衰减，但振荡剧烈，故必须校正。

2）对原系统进行滞后校正。按系统相角稳定裕度的要求，对系统进行滞后校正，并用以下MAT-LAB程序实现。

clear；k0=20；n1=[1]；d1=conv（conv（[12]，[23]），[1 0]）；

sope=tf（k0∗n1，d1）；gama=45；[Gc]=lagc（1，sope，[ga-ma]），

程序运行后得到PI调节器。

图13-65 未校正系统阶跃响应曲线

3）检查校正后系统跟随性能指标。用以下MATLAB程序检查校正后系统跟随性能指标。(www.xing528.com)

clear；k0=20；n1=[1]；d1=conv（conv（[12]，[23]），[10]）；s1=tf（k0∗n1，d1）；

n2=[15.991]；d2=[75.061]；s2=tf（n2，d2）；chec（2，s1，s2）；

程序运行后，可得校正后系统Bode图（见图13-66）与频域性能指标，还有如图13-67的校正后系统阶跃响应曲线。由计算数据可知校正系统频域性能指标：

幅值稳定裕度：L_h=13.3dB -π穿越频率：ω_g=1.68rad/s

相角稳定裕度：γ=45.4° 剪切频率：ω_c=0.628rad/s

图13-66 校正后系统的Bode图

图13-67 校正后系统阶跃响应曲线

由图13-67可见，校正后系统相角稳定裕度γ=45.4°>45°，满足要求；阶跃响应曲线超调量超过σ%=26.314%<30%，而且超调一次后，即刻衰减到稳态值。

4）进行阶跃扰动响应仿真。对系统图13-63所示的扰动，作等效变换，如图13-68所示。

图13-68 对系统图13-63扰动的等效变换

在图13-68d中，R（s）=0。根据不变性原理，要实现对扰动的完全补偿，则有，需。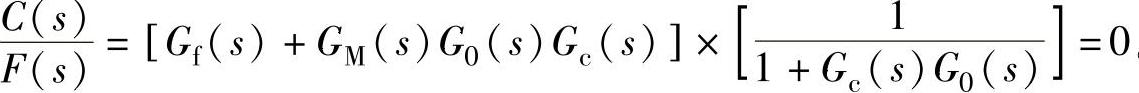

若G_f（s）+G_M（s）G₀（s）G_c（s）=0，就有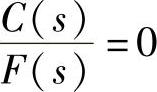，即要实现对扰动全补偿，需满足

为方便进行阶跃扰动响应的仿真，绘制出系统对于扰动的Simulink结构（见图13-69）即模型sx2L1309.mdl，图中PI调节器G_c（s）与G₀（s）串联。

图13-69 扰动信号作用的模型sx2L1309.mdl

根据过程控制原理^[25]，前馈—反馈控制系统对扰动完全补偿条件与前馈控制完全相同。

clear；[a，b，c，d]=linmod（sx2L1309）；

sys=ss（a，b，c，d）；step（sys），

程序执行后得到复合控制模型sx2L1309.mdl如图13-70所示的阶跃扰动响应曲线。由图可知，响应开始有些振荡，随着时间延续，阶跃扰动响应趋于零。这是根据不变性原理，实现了前馈控制对扰动的完全补偿，即系统被调量与对扰动作用完全无关。

图13-70 复合控制阶跃扰动响应曲线