简单回路控制系统的动态校正设计

过程控制中的单回路控制即简单控制系统，是由广义对象与调节器构成的负反馈闭环控制系统。工程实际中，单回路控制系统仍占过程控制总量的85%以上。

【例13-8】 已知过程控制系统被控广义对象为一个带延迟的惯性环节，其传递函数为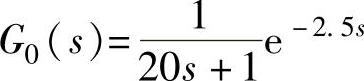，试用Ziegler-Nichols整定公式对系统进行PI、PID校正设计，校正后再施行Smith预估器控制并仿真。

解：1）检测未校正过程控制系统的频域性能指标。

clear；K=1；T=20；tau=2.5；n1=[K]；d1=[T 1]；G1=tf（n1，d1）；

[np，dp]=pade（tau，2）；Gp=tf（np，dp）；G=G1∗Gp；margin（G）；

程序运行后得到未校正过程控制系统的Bode图如图13-54所示。图中显示，未校正过程控制系统的相角稳定裕度为-180°，这样的系统不校正是绝对不行的。

2）用Ziegler-Nichols整定公式进行PI、PID校正设计。用Ziegler-Nichols整定公式进行PI、PID校正设计的MATLAB程序如下。

clear；K=1；T=20；tau=2.5；n1=[K]；d1=[T 1]；G1=tf（n1，d1）；

[np，dp]=pade（tau，2）；Gp=tf（np，dp）；

[Gc2，Kp2，Ti2]=zn01（2，[K，T，tau]）；

[Gc3，Kp3，Ti3，Td3]=zn01（3，[K，T，tau]）；

Gcc2=feedback（G1∗Gc2，Gp）；

set（Gcc2，Td，tau）；step（Gcc2）；hold on；

Gcc3=feedback（G1∗Gc3，Gp）；

set（Gcc3，Td，tau）；step（Gcc3）；

gtext（1 PI control），gtext（2 PID control），

程序运行后得到PI与PID调节器的传递函数分别为

程序运行后还绘制出校正系统的阶跃响应曲线，如图13-55所示。由曲线可看出，系统的超调量都超过60%，这样的时域响应指标是不能令人满意的。

图13-54 未校正过程控制系统的Bode图

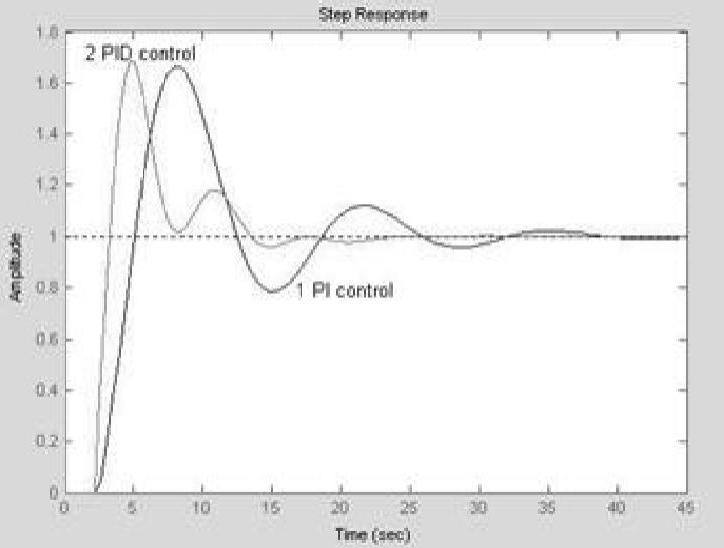
图13-55 校正后控制系统阶跃响应曲线

3）Smith预估器控制。

①Smith预估器控制原理等效变换。由《控制系统MATLAB计算及仿真》可知，Smith预估器控制的原理如图13-56所示。图中，G₀（s）e^-τs为广义对象数学模型，其中G₀（s）为不包含延迟时间τ的对象模型；G_c（s）为系统的一般PID调节器；G_s（s）为Smith预估补偿器，G_s（s）=G₀（s）（1-e^-τs）。

设C（s）=X₁，G_s（s）的输出为X₂，那么G_c（s）的输入量为R（s）-X₁-X₂。

当Smith（史密斯）预估器控制原理（见图13-56）画成图13-57时，G_c（s）的输入量仍然为R（s）-X₁-X₂，系统中其他方框传递函数与其输入输出量都不变，故两图等效。(www.xing528.com)

图13-56　Smith预估器控制原理图

图13-57　Smith预估器控制原理等效变换图

根据图13-57，有关系式

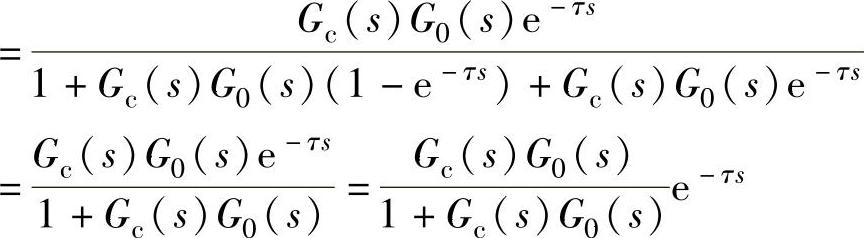
此关系式对应的等效动态结构图为图13-58，该图是以下仿真程序的依据。

图13-58　Smith预估器等效控制原理图

②PI与PID调节器校正后再施行Smith预估器控制。施行Smith预估器控制并仿真的MATLAB程序如下。

clear；K=1；T=20；tau=2.5；n1=[K]；d1=[T 1]；G1=tf（n1，d1）；[np，dp]=pade（tau，2）；Gp=tf（np，dp）；

n21=[59.947.2]；d21=[8.3250]；G21=tf（n21，d21）；n22=[60489.6]；d22=[050]；G22=tf（n22，d22）；

Gc1=feedback（G1∗G21，1）；Gc2=feedback（G1∗G22，1）；set（Gc1，Td，tau）；step（Gc1）；hold on；

set（Gc2，Td，tau）；step（Gc2），gtext（1 PI control），gtext（2 PID control），

程序运行后，还绘制出校正系统的阶跃响应曲线，如图13-59所示。由曲线可看出，系统阶跃响应的超调量都不超过10%，这样的时域指标非常优良，可见Smith控制的特殊作用。

图13-59 校正后施行Smith控制系统阶跃响应曲线

4）在Simulink中进行仿真。根据图13-57，做出系统用PI调节器校正后再施行Smith预估器控制的动态模型图sx2L1308.mdl（见图13-60）。

图13-60 系统动态模型sx2L1308.mdl

图13-60中模块“Step”为单位阶跃信号模块，即“Step time”设置为“0”，“Initial value”设置为“0”，“Final value”设置为“1”，“Sample time”设置为“0”；图中模块“Transport Delay”均为延迟模块，设置相同即“Time delay”设置为“2.5”，“Initial input”设置为“0”。图中模块“Scope”为示波器模块，将示波器模块工具栏按钮【Parameters】的卡片“General”中的“Time range”设置为“auto”，其他均为默认设置。如果需要，有时还要单击一下工具栏按钮【Autoscale】。

在“sx2L1308.mdl”模型窗口（见图13-60）中，先将工具栏的空白框【Simulationstop time】设置为“40”（秒）；然后执行菜单【Simulation】中的【Start】命令，即对模型系统进行阶跃给定响应仿真，再双击示波器图标即可得仿真结果曲线，如图13-61所示。可见，图13-61所示仿真曲线与通过程序仿真的阶跃响应（图13-59中的曲线1）是一样的。

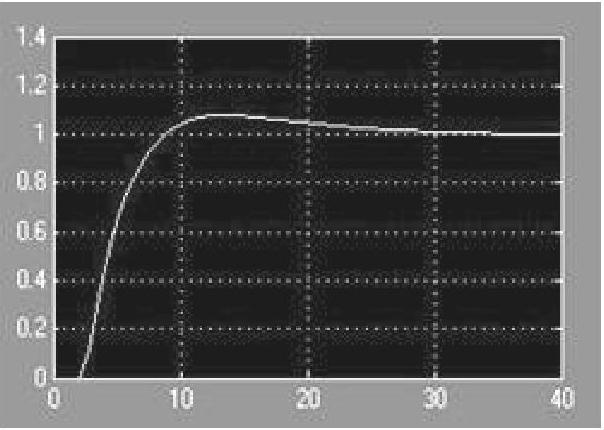
图13-61 单位阶跃响应仿真