由位置随动系统基本概念可知,位置随动系统的位置指令是经常变化的,是一个随机变量,而要求系统输出量准确跟随给定量的变化,系统输出响应的快速性、灵活性、准确性成了位置随动系统的主要特征。也就是说,系统跟随性能成了主要性能指标。
位置随动系统稳态运行时,希望输出量尽量复现输入量,即要求系统有一定的稳态误差精度,产生的位置误差越小越好,系统动态响应过程越快越好。影响系统稳态精度,导致系统产生稳态误差的原因有三种:一是由检测元件引起的检测误差;二是由系统结构与输入信号产生的原理误差;三是负载扰动产生的扰动误差。
1.检测误差
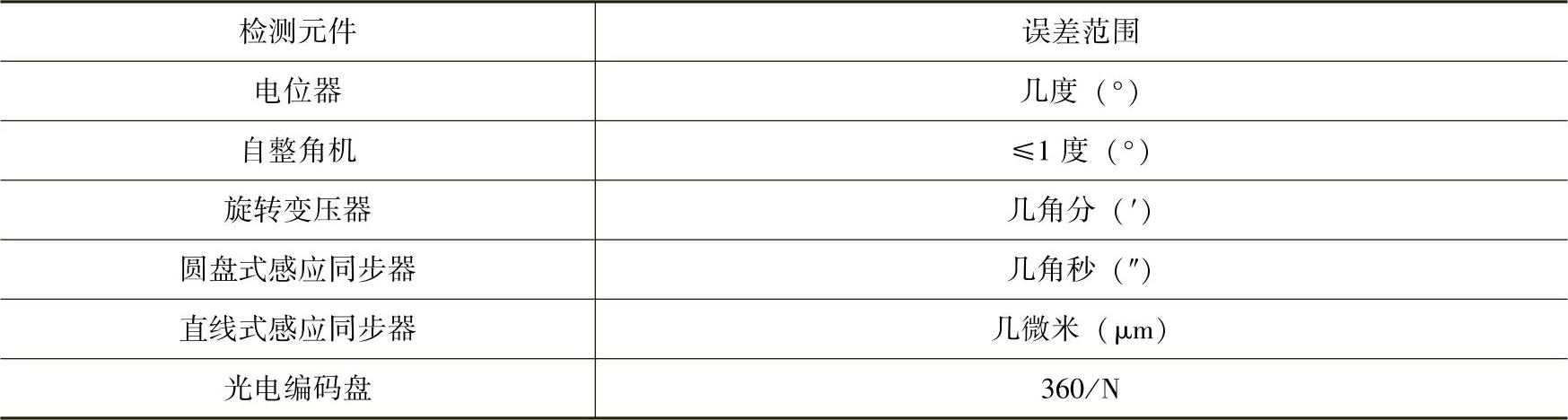
检测误差取决于检测元件本身精度,位置随动系统中常用位置检测元件如自整角机、旋转变压器、感应同步器等自身都有一定的精度等级,系统精度不可能高于所用位置检测元件的精度。检测误差是位置随动系统稳态误差的主要部分,是系统无法克服的。现将常用检测元件的误差列于表13-1中,以便选择使用时参考。
表13-1 常用检测元件的误差
2.原理误差
选择自整角机位置随动系统作为分析对象,其动态结构如图13-51所示。

图13-51 自整角机位置随动系统动态结构图
图13-51中,1)自整角机传递函数为比例环节,其比例(放大)系数为
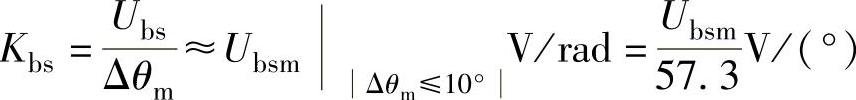
通常在|Δθm|≤10°的范围里,Kbs可认为是一恒值,常用的自整角机Kbs值约为0.6~1.2V/(°)。Ubsm是自整角机输出正弦电压振幅。θm∗-θm=|Δθm|,θm∗是发送机机械转角,θm是接收机机械转角。
2)相敏整流(放大)器为惯性环节,其传递函数为
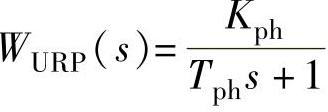
式中,Kph为相敏整流(放大)器放大系数;Tph为阻容滤波时间常数。
3)可逆功率放大器既可采用可逆晶闸管可控整流器(大功率随动系统),也可采用晶闸管脉冲调宽型(PWM)开关放大器(小功率随动系统),其传递函数为
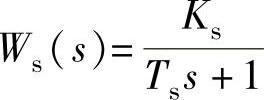
式中,Ks为晶闸管装置放大系数;Ts为晶闸管失控时间。
4)执行电机常采用直流伺服电机,其传递函数为振荡环节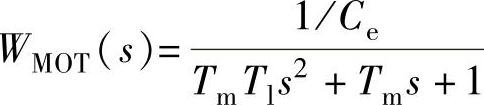 。
。
5)减速器对随动系统的工作有重大影响,减速器速比的选择与分配将影响到系统的惯性矩,并进而影响系统快速性。一般地说,减速器输入量是执行电机转速n,其单位常为r/min,减速器输出量是机械转角θm(°),其传递函数为一积分环节,即
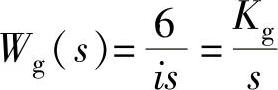
式中,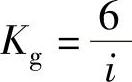 ,为减速器放大系数;i为减速器减速比。
,为减速器放大系数;i为减速器减速比。
6)如果把系统校正成Ⅱ型系统(一般情况都是如此),位置调节器APR应选用PI调节器,其传递函数为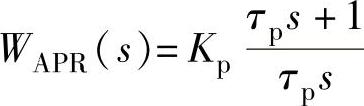 。
。
再将《控制系统MATLAB计算及仿真》中系统原理误差列于表13-2中。
表13-2 系统给定输入信号作用下的稳态误差(https://www.xing528.com)

表13-2中的K为闭环系统的开环增益,Kp、Kv、Ka分别为系统的静态位置误差系数、静态速度误差系数与静态加速度误差系数,并注意输入信号的量值系数r0、v0与a0。需要指出的是,表13-2中的数据是用Laplace变换终值定理推导出的,所以,有时直接用La-place变换终值定理求解稳态误差也是常见的。
3.扰动误差
表13-2中数据是系统原理误差,实际上随动系统所承受的各种扰动都会影响到系统的跟踪精度。最常见的扰动作用如图13-52所示。第一类是负载扰动,例如阵风对雷达天线是一种随机性负载扰动,轧机轧辊压下时的阻力是对压下随动系统的恒值负载扰动;第二类是系统参数发生变化,例如放大器零漂与元件老化或温度变化所引起的参数变化,以及电源电压波动等;第三类是噪声干扰,各种噪声干扰大都是从检测装置经反馈通道进入系统的。
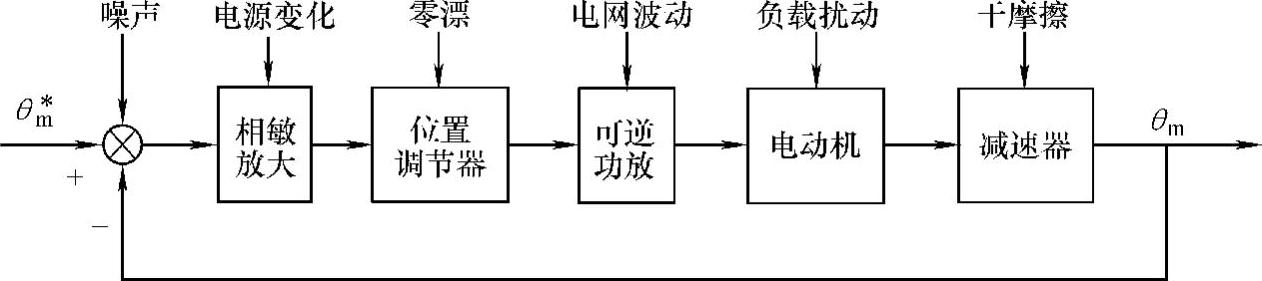
图13-52 位置随动系统中的扰动
除噪声干扰外,无论负载扰动还是参数扰动,尽管扰动的形式不同,但它们都作用在前向通道上,只是作用点不同,所以它们对系统产生的影响是相似的。
各种扰动引起的扰动误差,只要明确扰动的具体作用点,根据系统动态结构图,求出误差相对于扰动之间的传递函数,都可以用拉氏变换的终值定理来进行计算。
下面以恒负载扰动为例来说明其稳态误差的计算。
【例13-7】 自整角机位置随动系统结构如图13-53所示。已知系统数据如下:伺服电机为S661型,230W,110V,2.9A,2400r/min,Ra=3.4Ω;电枢回路总电阻R=5.1Ω,减速器速比i=60;自整角机放大系数Kbs=1.25V/(°);相敏与功放总增益KphKs=200;自整角机的检测误差ed=0.5°;实际负载转矩为TL=20N·m。试求输入轴为最高转速θ·m∗=200(°)/s时系统的稳态误差是多少?
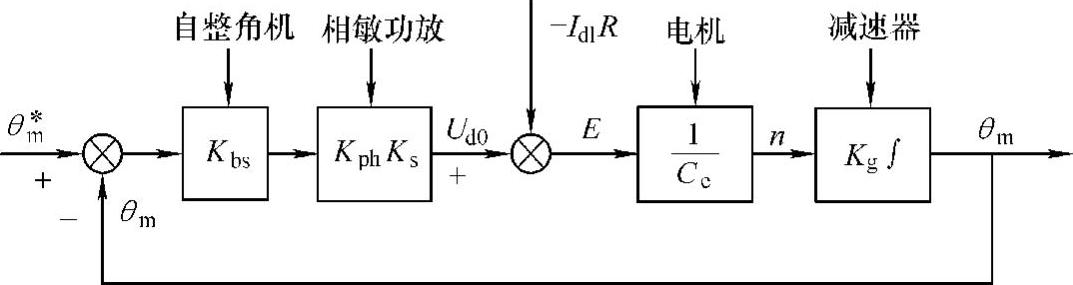
图13-53 自整角机位置随动系统静态结构图
解:1)系统检测误差ed。系统的检测误差就是自整角机的检测误差ed=0.5°。
2)系统原理误差esv。根据系统开环增益的概念,由图13-53可知,系统的开环增益为
K=KbsKphKsKg/Ce
已知Kbs=1.25V/(°);KphKs=200;Kg=6/i=6/60。
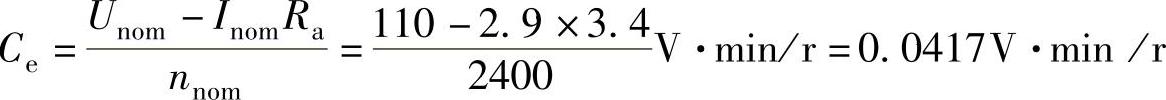
当θm∗=200t(°)时,θ·m∗=200(°)/s。若输入写成v(t)=v0t时,则v0=200(°)。那么esv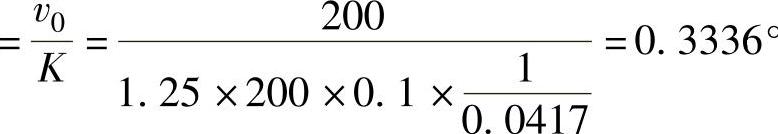 。
。
3)系统扰动误差et。根据自动控制原理[15],系统扰动误差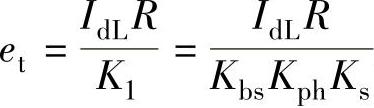 。式中,K1是误差信号到干扰作用点之间的增益。
。式中,K1是误差信号到干扰作用点之间的增益。
Cm=9.55Ce=9.55×0.0417N·m/A=0.398N·m/A
负载转矩折算到电动机轴上的等效转矩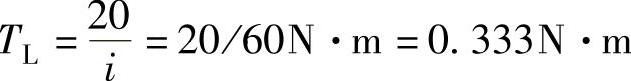 ,对应的负载电流
,对应的负载电流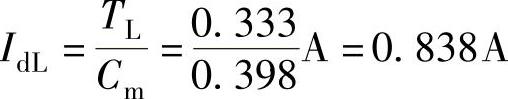 。
。
系统扰动误差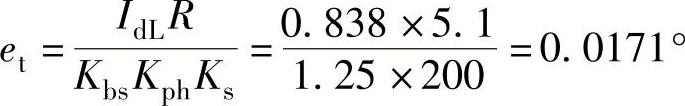 。
。
4)系统稳态误差ess。
ess=ed+esv+et=0.5°+0.3336°+0.0171°=0.8507°。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




