位置随动系统动态校正的设计优化

【例13-5】 某小功率随动系统，采用位置、转速与电流多环结构，其位置环结构如图13-40所示。图中相敏整流与滤波环节传递函数为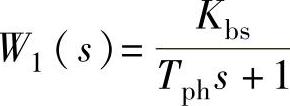，转速环等效闭环传递函数为，减速器传递函数。已知其中参数：K_bs=0.007V/（°）；T_ph=0.002s；T_Σn=0.01s；K₂=0.00025V·s/（°）；i=4。1）试设计一位置调节器，使系统满足下述指标：①在单位速度输入信号θ_m^∗=t（°）（t的单位为s）作用下，系统原理误差e_sv≤0.01°；②系统阶跃响应动态性能指标超调量σ%≤30%；调节时间t_s≤0.3s。2）再设计一位置调节器，使系统满足下述指标：①在单位加速度信号θ_m^∗=t²/2（°）（t的单位为s）作用下，系统误差e_sa≤0.01°；②系统阶跃响应动态性能指标超调量σ%≤30%；调节时间t_s≤0.3s。

图13-40 某小功率随动系统结构图

解：1）带入参数的系统环节传递函数。、、。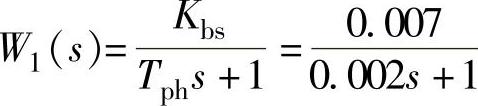

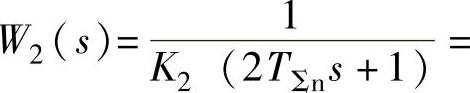
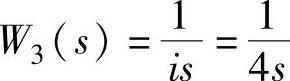未校正系统的开环传递函数为

2）求K、K₀与K_c。

根据自动控制理论与题意，本题给定系统为Ⅰ型系统，单位斜坡输入时，系统原理误差e_ss≤0.01°，即有。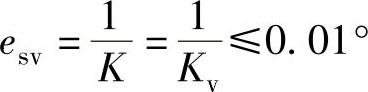

式中，K是系统开环增益，那么满足系统稳态性能指标要求的开环传递函数为

由K₀=7，位置调节器的增益。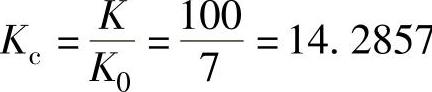

3）被控对象的传递函数。被控对象传递函数为，而满足系统稳态性能指标要求的开环传递函数为。

4）作原系统的Bode图与阶跃响应曲线，检查是否满足题目要求。根据系统校正设计的步骤，首先检查原系统的频域性能指标是否满足题目要求，并观察其阶跃响应曲线形状。为此给出如下调用自编函数chec.m列写的程序。

clear；K=100；n1=1；d1=conv（conv（[10]，[0.021]），[0.0021]）；

s1=tf（K∗n1，d1）；s2=[]；chec（1，s1，s2）；

程序运行后，可得未校正系统的Bode图与频域性能如图13-41所示，还有如图13-42所示的未校正系统的阶跃响应曲线。

由计算数据可知未校正系统的频域性能指标：

幅值稳定裕度：L_h=14.8dB -π穿越频率：ω_g=158rad/s

相角稳定裕度：γ=31.7° 剪切频率：ω_c=62.2rad/s

图13-41 未校正系统的Bode图与频域性能

图13-42 未校正系统的单位阶跃响应曲线

从计算的数据看，频域性能指标尚可，但是图13-42所示系统阶跃响应曲线表明，系统超调量σ%≈40%>30%，不满足题目要求，必须校正。

5）求滞后校正器的传递函数。可将时域性能指标超调量σ%=30%转换为频域性能指标相角裕度γ。

clear；sigma=30；[gama]=sitoga（sigma）；gama=vpa（gama∗180/pi，4），

程序运行后可知超调量σ%=30%，相当于相角裕度γ=43.42°。

将惯性环节时间常数0.002s改为0.2s并作恒等变换后，MATLAB 7.5版本系统能运行以下调用自编函数lagc.m的程序求校正补偿器传递函数。

clear；K=10000；n1=1；d1=conv（conv（[10]，[0.021]），[0.2100]）；

sope=tf（K∗n1，d1）；gama=48；[Gc]=lagc（1，sope，[gama]），

程序运行后得到的传递函数（包括增益）为。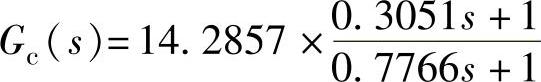

6）校验系统校正后频域与时域性能指标是否满足题目要求。系统包含有校正器的系统传递函数为

①由系统的开环增益K=100，可知系统原理误差；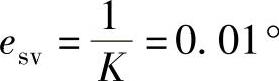

②根据校正后系统的结构与参数，计算系统校正后频域与时域性能指标。

clear；K=100；n1=1；d1=conv（conv（[10]，[0.021]），[0.0021]）；s1=tf（K∗n1，d1）；

n2=[0.30511]；d2=[0.77661]；s2=tf（n2，d2）；chec（2，s1，s2）；

程序运行后，可得校正后系统的Bode图如图13-43所示。由图可知系统的：

幅值稳定裕度：L_h=22.5dB -π穿越频率：ω_g=155rad/s

相角稳定裕度：γ=49.5° 剪切频率：ω_c=32.9rad/s

图13-43 校正后系统的Bode图

图13-44 校正后系统单位阶跃响应曲线

程序运行后，有校正后系统的单位阶跃响应曲线（见图13-44）及校正后系统的阶跃响应品质指标：超调量σ%=19.8085%；峰值时间t_p=0.0920s；调节时间（5%）t_s=0.1227s。

7）位置调节器G_c（s）=14.2857×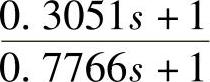的说明。此位置调节器能使系统在跟踪单位速度输入信号θ_m^∗=t（°）时，系统原理误差e_ss≤0.01°。系统校正前为Ⅰ型系统，经串联滞后校正后，仍为Ⅰ型系统，即系统对于给定输入信号只有Ⅰ型稳态精度。当然，系统也满足了其他指标要求。

8）将系统校正成Ⅱ型系统。根据题目要求系统能跟踪加速度输入，故应把系统校正成Ⅱ型系统。系统对象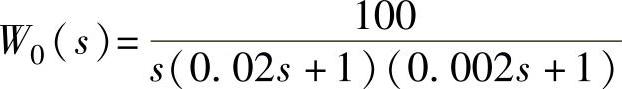，两个惯性环节时间常数均较小，根据自控系统理论^[21]，位置调节器APR应选用PI调节器，其传递函数为W_APR（s）=。

根据自动控制理论^[21]，由给定系统阶跃响应超调量，根据系统被控对象为积分环节加两个惯性环节，选择系统中频宽度的设计方法，给出调用以下自编函数prxd1.m的MATLAB程序来计算位置调节器传递函数。

clear；Kbs=0.007；K2=0.00025；i=4；Kobj=Kbs/（K2∗i）；

Tph=0.002；Tsigman=0.01；Tsigma=2∗Tsigman+Tph；

sigma=0.3；[Kp，taup]=prxd1（sigma，[Kobj，Tsigma]）；

程序运行后得到位置调节器APR的传递函数为

图13-45 校正成Ⅱ型系统的Bode图(www.xing528.com)

9）校正成的Ⅱ型系统是否满足题目要求。

①检验在单位加速度信号θ_m∗=t²/2（°）作用下的系统原理误差。

根据自动控制理论，由单位加速度信号θ_m∗=t²/2（°）作用下的系统原理误差计算公式以及系统开环增益的概念，给出以下MATLAB程序。

clear；Kbs=0.007；K2=0.00025；i=4；Kp=3.7106；

taup=0.1540；K=Kbs∗Kp/（K2∗i∗taup），esa=1/K，

程序运行后得到开环增益K=168.6636s^-2，原理误差e_sa=0.0059°≤0.01°。

②检验系统阶跃响应动态性能指标（超调量与调节时间）。

用以下MATLAB程序来计算系统阶跃响应的超调量与调节时间。

clear；K=7；n1=1；d1=conv（conv（[10]，[0.021]），[0.0021]）；s1=tf（K∗n1，d1）；

n2=[0.1541]；d2=[0.04150]；s2=tf（n2，d2）；chec（2，s1，s2）；

程序运行后，可得校正后系统Bode图如图13-45所示。程序运行后还绘制校正后系统单位阶跃响应曲线（见图13-46）及校正后系统阶跃响应品质指标：超调量σ%=29.7144%<30%；峰值时间t_p=0.1176s；调节时间（5%）t_s=0.2353s<0.3s。

【例13-6】 已知随动系统固有部分传递函数为，式中K_obj=15；T_m=0.2s；Tl=0.02s。要求设计一调节器，使系统满足下述性能指标：1）加速度品质因数K_a≥120s^-2；2）系统阶跃响应超调量σ%≤30%；调节时间t_s≤0.3s。

图13-46 校正成Ⅱ型系统的单位阶跃响应曲线

解：1）被控对象传递函数为。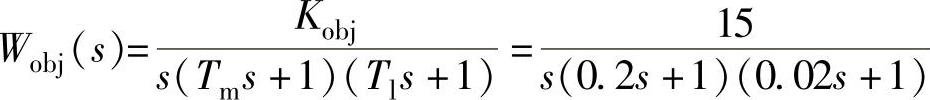

根据题意，有K_a=K≥120s^-2。满足系统稳态性能指标要求的开环传递函数应为。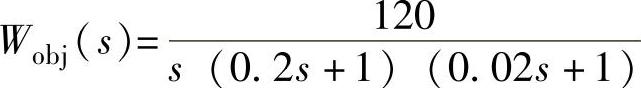

需要说明的是，系统加速度品质因数为120s^-2，对应着Ⅱ型系统。未校正系统为Ⅰ型系统，现将此数据作为设计系统调节器的Bode图与阶跃响应的参考依据。

2）作原系统的Bode图与阶跃响应曲线，检查是否满足题目要求。根据系统校正设计的步骤，首先检查原系统的频域性能指标是否满足题目要求，并观察其阶跃响应曲线形状。为此给出如下调用自编函数chec.m列写的程序。

clear；K=120；n1=1；d1=conv（conv（[10]，[0.21]），[0.021]）；

s1=tf（K∗n1，d1）；s2=[]；chec（1，s1，s2）；

程序运行后，可得未校正系统的Bode图与频域性能如图13-47所示，还有如图13-48所示的未校正系统阶跃响应曲线。由计算数据可知未校正系统的频域性能指标：

幅值稳定裕度：L_h=-6.78dB -π穿越频率：ω_g=15.8rad/s

相角稳定裕度：γ=-12.5° 剪切频率：ω_c=23.1rad/s

图13-47 未校正系统的Bode图

图13-48 未校正系统单位阶跃响应曲线

计算表明，幅值稳定裕度与相角稳定裕度都为负值，这样的系统是不稳定的。再从图13-48可以看到，系统阶跃响应曲线呈现发散的振荡。这都说明系统不满足要求，必须校正。

3）将系统校正成Ⅱ型系统。因为要求系统能跟踪加速度输入，故应把系统校正成Ⅱ型系统，位置调节器APR应选用PID调节器，其传递函数为。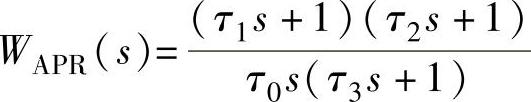

根据随动系统校正设计理论，由给定系统阶跃响应超调量与系统被控对象为积分环节加两个惯性环节，选择系统中频宽度的设计方法，给出以下调用自编函数prxd2.m（当位置环的控制对象为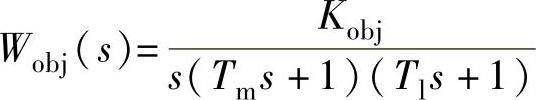时，由给定系统阶跃响应超调量σ%，选择系统中频宽度h，并将系统校正成Ⅱ型系统时，设计位置随动系统位置调节器的函数）的MAT-LAB程序来计算位置调节器传递函数。

clear；Kobj=15；Tm=0.2；Tl=0.02；tau3=0.005；sigma=0.3；

T2=Tl+tau3；[tau0，tau1，tau2]=prxd2（sigma，[Kobj，Tm，Tl，tau3]）；

程序运行后得到位置调节器APR传递函数为

4）校正成的Ⅱ型系统是否满足题目要求。

①检验系统加速度品质因数。根据自动控制理论，Ⅱ型系统加速度品质因数与系统开环增益概念，给出以下程序。

clear；Kobj=15；tau0=0.1148；K=Kobj/tau0；Ka=K，

程序运行后得到加速度品质因数K_a=K=130.6620s^-2>120s^-2，满足题目要求。

②检验系统阶跃响应动态性能指标（超调量与调节时间）。

clear；K=15；n1=1；d1=conv（conv（[10]，[0.21]），[0.021]）；

s1=tf（K∗n1，d1）；K2=1/0.1148；n2=conv（[0.21]，[0.1751]）；

d2=conv（[10]，[0.0051]）；s2=tf（K2∗n2，d2）；chec（2，s1，s2）；

程序运行后，可得校正系统的Bode图与频域性能如图13-49所示，还有如图13-50所示的校正系统阶跃响应曲线。由计算数据可知未校正系统的频域性能指标：

幅值稳定裕度：L_h=19.4dB -π穿越频率：ω_g=92.6rad/s

相角稳定裕度：γ=45.7° 剪切频率：ω_c=21.6rad/s

图13-49 校正成Ⅱ型系统的Bode图

计算数据表明，校正后系统稳定裕度足够大。程序运行后还得到校正后系统的单位阶跃响应曲线（见图13-50）及其系统的阶跃响应指标：超调量σ%=30.5729%≈30%；峰值时间t_p=0.1332s；调节时间（5%）t_s=0.2715s<0.3s。可见校正后系统基本满足题目要求。

图13-50 校正成Ⅱ型系统的单位阶跃响应曲线