MATLAB仿真：多闭环控制系统计算与优化

《控制系统MATLAB计算及仿真》对多环调速系统进行了各种给定输入响应仿真，特别是对双闭环控制系统仿真作了全面介绍。在此，着重介绍带转速微分负反馈双闭环调速系统的仿真。

根据自动控制系统设计理论，ACR、ASR均采用PI调节器的双闭环调速系统具有良好的稳态与动态性能，结构简单，工作可靠，设计也很方便，实践证明，它是一种应用最广的调速系统。然而，其动态性能不足之处就是转速超调，而且抗扰性能的提高也受到一定限制。

解决这个问题的一个简单有效办法就是在转速调节器上引入转速微分负反馈，这样就可以抑制转速超调直到消灭超调，同时可以大大降低动态速度降落。请看以下示例。

【例13-2】 带转速微分负反馈的晶闸管—直流电机双闭环调速V-M系统动态结构图如图13-20所示。图中电机参数：P_nom=40kW，n_nom=1000r/min，U_nom=440V，I_nom=104A，电机电枢电阻R_a=0.3Ω，V-M系统主电路总电阻R=0.5Ω，电枢主电路总电感L=200mH，拖动系统运动部分飞轮矩GD²=77.5N·m²，过载电流倍数λ=2，三相桥平均失控时间T_s=0.00167s，要求系统调速范围D=20，静差率s=10%，堵转（最大）电流I_dbl=2.1I_nom，临界截止电流I_dcr=2I_nom。ACR、ASR均采用PI调节器，ASR限幅输出U^∗_im=-8V，ACR限幅输出U_ctm=8V，若U_n^∗=10V时，n=n_nom=1000r/min。1）试计算系统参数：电机电动势转速比C_e、触发整流装置放大系数K_s、电流反馈系数β、系统机电时间常数T_m、系统测速反馈系数α；2）估算主电路的总电感与电枢回路电磁时间常数T_a；3）选择几个时间常数T_0i、T_0n、T_0dn与中频宽h；4）计算电流调节器传递函数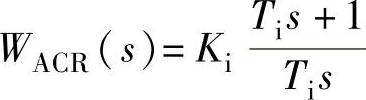；5）计算转速调节器传递函数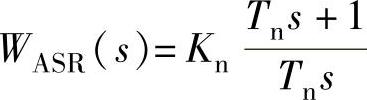；6）对双闭环调速系统进行单位阶跃响应仿真与单位阶跃负载扰动响应仿真；7）对转速微分负反馈环节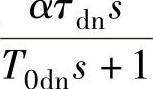进行参数计算；8）对带转速微分负反馈双闭环调速系统进行单位阶跃响应仿真与单位阶跃负载扰动响应仿真；9）对6）与8）两项仿真作简单比较；10）计算退饱和时间t_t与退饱和转速n_t。

图13-20 双闭环调速系统原理图

解：1）拖动调速系统几个参数的计算与选择。

①额定磁通下的电机电动势转速比。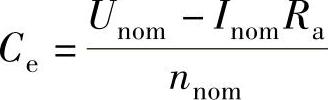

clear；syms Unom Inom nnom Ra Ce；

Unom=440；Inom=104；Ra=0.3；nnom=1000；

Ce=（Unom-Inom∗Ra）/nnom，

程序运行后得到额定磁通下电机电动势转速比C_e=0.4088V·min/r。

②满足系统要求时的触发整流装置放大系数。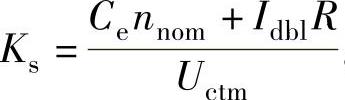

clear；syms Ks nnom Ibdl R Ce Uctm；

Ce=0.4088；nnom=1000；Idbl=2∗104；R=0.5；Uctm=8；

Ks=（Ce∗nnom+Idbl∗R）/Uctm，

程序运行后得到系统要求的触发整流装置放大系数K_s=64。

③满足系统要求的电流反馈系数。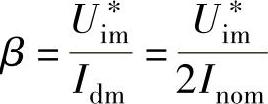

clear；syms beta Uim Idm Inom；Uim=8；

Inom=104；Idm=2∗Inom；beta=Uim/Idm，

程序运行后得到满足系统要求的电流反馈系数β=0.0385V/A。

④电机拖动系统机电时间常数。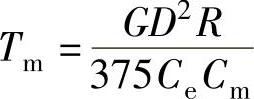

clear；syms GDpf R Ce Cm；GDpf=77.5；R=0.5；

Ce=0.4088；Cm=30∗Ce/pi；Tm=（GDpf∗R）/（375∗Ce∗Cm），

程序运行后得到电机拖动系统机电时间常数T_m=0.0648s。

⑤满足系统要求的转速反馈系数。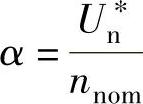

clear；syms alpha Un nnom；Un=10；nnom=1000；alpha=Un/nnom，

程序运行后得到满足系统要求的转速反馈系数α=0.01V·min/r。

⑥选取电流环滤波时间常数T_0i=0.002s；选取转速环滤波时间常数T_0n=0.01s；选取转速微分滤波时间常数T_0dn=T_0n=0.01s；选择中频宽h=5。

2）电枢回路电磁时间常数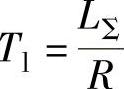。根据参考文献[32]提供的公式，先估算各种电感量，然后计算电枢回路电磁时间常数。

①电枢电感量。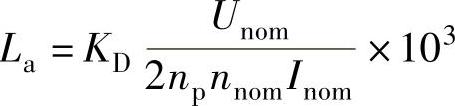

式中，U_nom为电机额定电压；n_p为电机磁极对数；n_nom为电机额定转速；I_nom为电机额定电流；K_D为计算系数，无补偿绕组时K_D=8～12，此处取K_D=10。

clear；syms La KD Unom np nnom Inom；

KD=10；Unom=440；np=3；nnom=1000；Inom=104；

La=KD∗Unom∗10^3/（2∗np∗nnom∗Inom），

程序运行后得到电枢电感量。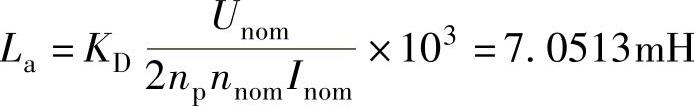

②整流变压器的电感量。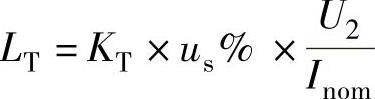

式中，u_s%为整流变压器短路电压百分数，一般取u_s%=5%；U₂为整流变压器二次侧额定相电压，这里取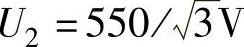；I_nom为电动机额定电流I_nom=104A；K_T为与整流电路形式有关的计算系数，三相全控桥K_T=3.9，三相零式K_T=6.75，单相全控桥K_T=3.18。取K_T=3.9、u_s%=5%、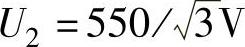、I_nom=104A，则L_T=0.5954mH。

③限制电流脉动的电感量。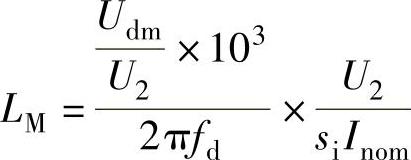

式中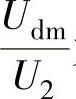，为整流电压最低谐波的幅值与电源相电压之比，与整流电路的形式有关，三相全控桥为0.46，三相零式为0.88，单相全控桥为1.2；f_d为整流电流的最低谐波频率，与整流电路的形式有关，三相全控桥f_d=300Hz，三相零式f_d=150Hz，单相全控桥f_d=100Hz；s_i为电流脉动系数，这里取s_i=0.05。

最后有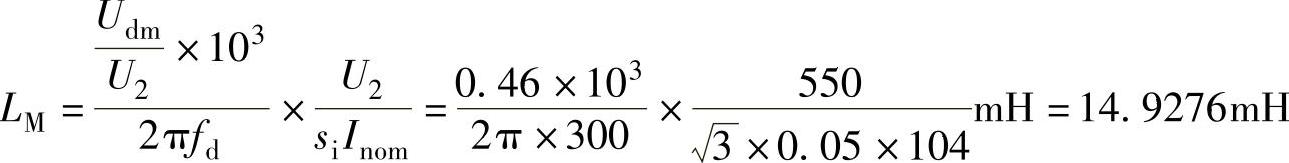

④与负载串联的限制电流脉动的实际电感量L=L_M-（L_a+2L_T）。

L=L_M-（L_a+2L_T）=15mH-（7.0513+2×0.5954）mH=6.7579mH

⑤主电路总电感量。

L_Σ=L_a+2L_T+L=7.0513mH+2×0.5954mH+6.7579mH=15mH

⑥电枢回路电磁时间常数。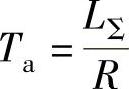

clear；syms TL R Lsigma；Lsigma=15∗10^（-3）；R=0.5；TL=Lsigma/R，

程序运行后得到电枢回路电磁时间常数T_a=0.03s。

3）电流调节器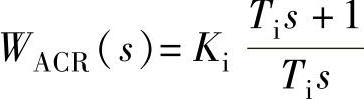参数计算。根据自动控制系统设计理论，选取电流环滤波时间常数T_0i=0.002s；选取积分时间常数T_i=T_a=0.03s，三相桥整流电路平均失控时间T_s=0.00167s，合并电流环小时间常数T_Σi=T_s+T_0i=0.00167s+0.002s=0.00367s，电流环开环增益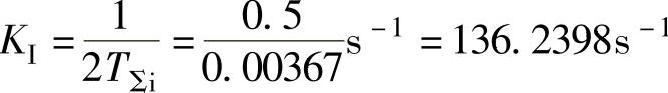，电流调节器的比例系数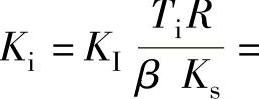0.8294，所以电流调节器传递函数为。

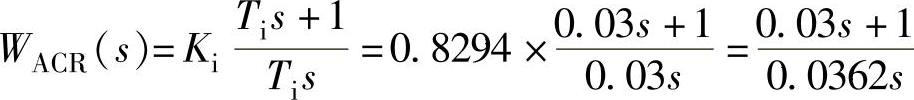选取转速环滤波时间常数T_0n=0.01s、转速微分滤波时间常数T_0dn=T_0n=0.01s；选择中频宽h=5。

4）转速调节器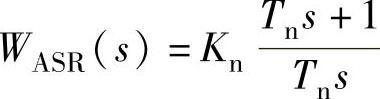参数计算。根据自动控制系统设计理论，选取转速环滤波时间常数T_0n=0.01s；以上已经确定T_Σi=0.00367s，合并转速环小时间常数则为T_Σn=2T_Σi+T_0n=2×0.00367s+0.01s=0.0173s；选择中频宽h=5；选取转速调节器积分时间常数T_n=hT_Σn=5×0.0173s=0.0865s；转速环开环增益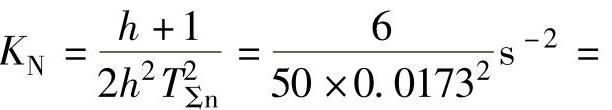400.95s^-2；转速调节器比例系数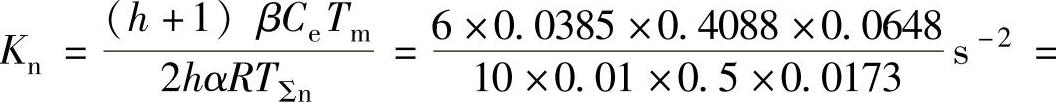7.0743s^-2。所以转速调节器传递函数。

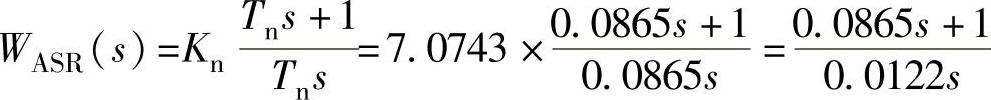5）双闭环调速系统的Simulink动态结构图及其仿真。

①创建带参数双闭环调速系统模型sx2L1302.mdl，如图13-21所示。

根据图13-20，图13-21中。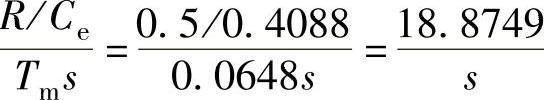

图13-21 带参数的双闭环调速系统模型sx2L1302.mdl(www.xing528.com)

②双闭环调速系统单位阶跃响应仿真。

clear；[a，b，c，d]=linmod（sx2L1302）；

s1=ss（a，b，c，d）；sys=tf（s1）；step（sys），

[y，t]=step（sys）；perf（2，y，t）；

程序运行后绘制的单位阶跃响应曲线如图13-22所示。还算得双环系统单位阶跃响应的超调σ%=36.2266%、峰值时间t_p=0.0847s、调节时间t_s=0.2091s。

③创建双闭环调速系统负载扰动仿真动态结构图sx2L1302a.mdl，如图13-23所示。

④双闭环调速系统单位阶跃负载扰动响应仿真。

图13-22 双环调速系统单位阶跃响应曲线

图13-23 双闭环调速系统负载扰动仿真动态结构图sx2L1302a.mdl

clear；[a，b，c，d]=linmod（sx2L1302a）；s1=ss（a，b，c，d）；t1=[0：0.01：2]；

[y，t]=step（s1，t1）；step（s1，t1）；[detac，tp，tv]=dist（1，y，t），

程序运行后绘制单位阶跃负载扰动响应曲线，如图13-24所示，并计算出性能指标，即无基准量最大动态降落：Δc_max%=-0.5258%，最大动态降落时间：t_p=0.05s，恢复时间：t_v=0.16s（对应5%的误差带）。

特别提请读者注意，如果模型sx2L1302a.mdl在work目录下的子目录里，运行此程序时，模型sx2L1302a.mdl必须处于打开状态。同时MATLAB系统必须停留在work里。

6）带转速微分负反馈的转速调节器的原理图与电流关系式。

带转速微分负反馈的转速调节器原理图如图13-25所示。

由图13-25，根据欧姆定理，流经C_dn、R_dn转速微分负反馈支路电流象函数为

图13-24 双环系统单位阶跃负载扰动响应曲线

图13-25 带转速微分负反馈的转速调节器原理图

在图13-25中对虚地点A写出Kirchhoff电流定理^[21]：

整理后得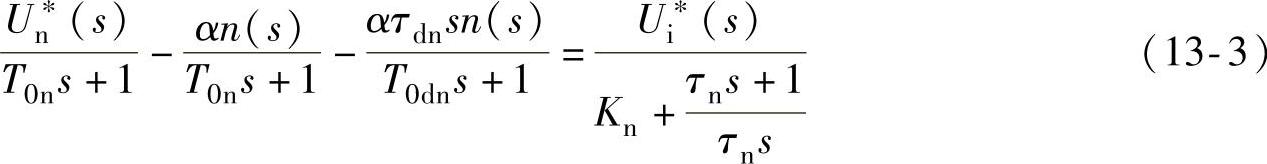

式中，τ_dn=R₀C_dn，为转速微分时间常数；T_0dn=R_dnC_dn，为转速微分滤波时间常数。

7）转速微分负反馈环节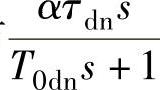参数的计算。

已经计算出转速反馈系数α=0.01V·min/r。根据自动控制系统设计理论[21]，选取转速微分滤波时间常数T_0dn=T_0n=0.01s。

取τ_dn=0.0634s，那么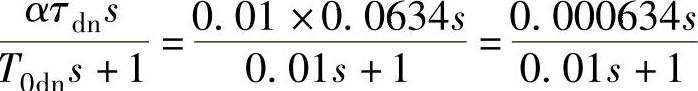

8）带参数转速微分负反馈双闭环调速系统的Simulink动态结构图。

①创建转速微分负反馈双环系统负载扰动仿真模型sx2L1302b.mdl，如图13-26所示。

根据图13-21所示的模型sx2L1302.mdl，将算得的转速微分负反馈环节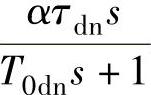参数带入即得模型sx2L1302b.mdl，以下仿真要用到它。

图13-26 带转速微分负反馈环节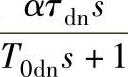的系统模型sx2L1302b.mdl

②转速微分负反馈双闭环调速系统的单位阶跃响应仿真。

clear；[a，b，c，d]=linmod（sx2L1302b）；

s1=ss（a，b，c，d）；sys=tf（s1）；step（sys），

[y，t]=step（sys）；perf（2，y，t）；

程序运行后绘制的单位阶跃响应曲线如图13-27所示。由图可见，双环系统单位阶跃响应的超调σ%=36.2266%；而带转速微分负反馈的双环系统σ%=3.2922%，超调大为降低，转速微分负反馈作用显示无疑。

③创建转速微分负反馈双闭环系统负载扰动仿真模型sx2L1302c.mdl，如图13-28所示，以下仿真要用到它。

图13-27 转速微分负反馈双环系统单位阶跃响应曲线

图13-28 转速微分负反馈双闭环调速系统负载扰动仿真模型sx2L1302c.mdl

④转速微分负反馈双闭环调速系统的单位阶跃负载扰动响应仿真。

clear；[a，b，c，d]=linmod（sx2L1302c）；

s1=ss（a，b，c，d）；t1=[0：0.01：2]；

[y，t]=step（s1，t1）；step（s1，t1）；

[detac，tp，tv]=dist（1，y，t），

程序运行后绘制的单位阶跃负载扰动响应曲线如图13-29所示，比较图13-24与图13-29及其计算的数据，带转速微分负反馈双环系统比普通双环系统，其单位阶跃负载扰动无基准量最大动态降落从-0.5258%下降为-0.2305%；最大动态降落时间t_p=0.05s上升到t_p=0.07s，恢复时间t_v=0.16s上升到t_v=0.29s。

9）计算退饱和时间t_t与退饱和转速n_t。根据自动控制系统设计理论^[21]，有退饱和时间计算公式tt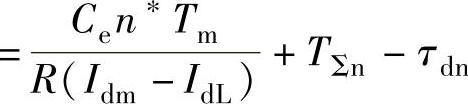，还有退饱和转速计算公式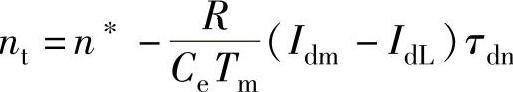。这可以用以下MAT-

LAB程序来计算退饱和时间t_t与退饱和转速n_t：

clear；syms Ce nx Tm R Idm Idbl Inom IdL Tsigman taudn tt；

Ce=0.4088；nx=1000；Tm=0.0648；R=0.5；Inom=104；Idbl

=2∗Inom；

Idm=Idbl；IdL=0；Tsigman=0.0173；taudn=0.0634；

tt=Ce∗nx∗Tm/（R∗（Idm-IdL））+Tsigman-taudn，

nt=nx-R∗（Idm-IdL）∗taudn/（Ce∗Tm），

程序执行后得到退饱和时间t_t=0.2086s，退饱和转速n_t=751.0932r/min。

图13-29 转速微分负反馈双环系统单位阶跃负载扰动响应曲线