MATLAB仿真：简单闭环控制计算与实现

图13-1 转速单闭环调速系统的Simulink动态结构图

《控制系统MATLAB计算及仿真》中对简单闭环控制调速系统进行了各种给定输入信号响应仿真。在此，将对简单闭环控制调速系统，再应用作者自编程序，进行PI校正设计，并验算设计后系统时域与频域性能指标是否满足要求。请看以下示例。

【例13-1】 已知龙门刨床工作台拖动系统采用晶闸管—直流电机单闭环调速系统（V-M系统）Simulink动态结构图如图13-1所示。图中电机参数：P_nom=60kW，n_nom=1000r/min，U_nom=220V，I_nom=305A，电枢电阻R_a=0.056Ω，V-M系统主电路总电阻R=0.18Ω，电枢电磁时间常数T_a=0.012s，系统运动部分飞轮矩对应的机电时间常数T_m=0.097s，整流触发装置的放大系数K_s=40，三相桥平均失控时间T_s=0.00167s。1）试计算额定磁通下电机电动势转速比；2）要求系统调速范围D=20，静差率s=5%，求闭环系统开环放大系数K；3）若U_n∗=12V时n=n_nom=1000r/min，求拖动系统测速反馈系数K_t或α；4）计算满足系统调速范围与静差率要求的比例调节器放大系数K_p；5）试问系统此时能否稳定运行？其临界开环放大系数K_cr为多少？6）试绘制出系统开环放大系数大于K_cr与小于K_cr（改变系统比例调节器K_p的设置）时系统单位给定阶跃响应曲线以验证系统能否稳定运行？7）以相角稳定裕度为校正主要指标对系统进行滞后校正；8）以剪切频率为校正主要指标对系统进行滞后校正；9）用根轨迹校正器对系统进行滞后校正。

解：1）计算C_e、Δn_cl、Δn_op、K。

clear；Unom=220；Inom=305；nnom=1000；s=0.05；D=20；R=0.18；Ra=0.056；

[Ce，delnnom，delncl，delnop，K]=closeK（Unom，Inom，nnom，Ra，R，D，s）；

程序运行后得到额定磁通下电机电动势转速比C_e=0.2029V·min/r、满足系统调速范围与静差率要求时的闭环系统稳态速降Δn_cl=Δn_nom=2.6316r/min、系统开环额定负载下稳态速降Δn_op=270.55r/min、满足系统调速范围与静差率要求的闭环系统开环放大系数K=101.8090。

图13-2 单闭环调速系统静态结构图

2）求系统测速反馈系数。

对单闭环调速系统有静态结构图如图13-2所示。根据自动控制理论有如下方程组

式中，K=K_pK_sα/C_e。

代入已知条件得到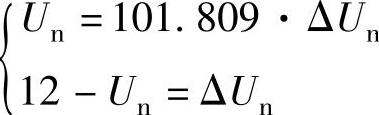

用MATLAB程序解此方程组

clear；syms Un delUn alpha；

[Un，delUn]=solve（Un=101.809∗delUn，12-Un=delUn）；

alpha=vpa（Un/1000，4），

程序运行结果K_t=α=0.01188V·min/r（因为MATLAB模型图中不能输入希腊字母，图13-1中测速反馈系数为K_t）。

3）计算比例调节器放大系数K_p。根据自动控制理论，闭环系统开环放大系数K、测速反馈系数α、电机电动势转速比C_e与放大系数K_p之间满足关系式：K=K_pK_sα/C_e。

clear；syms K Kp Ks Ce alpha；K=101.809；Ks=40；

Ce=0.2029；alpha=0.01188；Kp=（K∗Ce）/（Ks∗alpha），

程序运行结果K_p=43.4702。

4）绘制单闭环调速系统Simulink动态结构图模型sx2L1301.mdl，如图13-3所示。

图13-3 带参数单闭环调速系统的动态结构图模型sx2L1301.mdl

5）求闭环系统临界开环放大系数。

根据自动控制理论的代数判据，系统稳定的充要条件为，其临界开环放大系数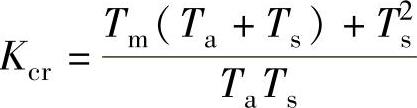。式中，T_m是系统运动部分飞轮矩相应的机电时间常数，T_a是电枢回路电磁时间常数，T_s是三相桥平均失控时间。

clear；Tm=0.097；Ta=0.012；Ts=0.00167；Kcr=（Tm∗（Ta+Ts）+Ts^2）/（Ta∗Ts），

程序运行后得到闭环系统临界开环放大系数K_cr=66.3063。

6）求系统闭环特征根以验证系统能否稳定运行。

clear；[a，b，c，d]=linmod（sx2L1301）；s1=ss（a，b，c，d）；

sys=tf（s1）；sys1=zpk（s1）；P=sys.den{1}；roots（P），

程序运行后得到

ans=

1.0e+002∗-7.1466

0.1626+2.7155i

0.1626-2.7155i

即系统闭环特征根有两个根的实部为正，说明系统不能稳定运行。

7）对应临界开环放大系数K_cr=66.3063，计算其对应的K_p。

clear；syms K Kp Ks Ce alpha；K=66.3063；Ks=40；

Ce=0.2029；alpha=0.01188；Kp=（K∗Ce）/（Ks∗alpha），

程序运行后得到K_p=28.3113。以下将绘制临界值两侧（K_p=28与K_p=28.312）系统的单位给定阶跃响应曲线以验证系统能否稳定运行。

①绘制比例调节器K_p=28时系统模型sx2L1301a.mdl，如图13-4所示，并用程序绘制系统的阶跃响应曲线。

图13-4 比例调节器K_p=28时系统模型sx2L1301a.mdl

clear；[a，b，c，d]=linmod（sx2L1301a）；

s1=ss（a，b，c，d）；sys=tf（s1）；step（sys），

程序运行后得到当K_p=28时对应着模型sx2L1301a.mdl绘制的系统单位阶跃响应曲线，如图13-5所示，呈现剧烈的衰减振荡，尚属于稳定系统范围。

②绘制比例调节器K_p=28.312时系统模型sx2L1301b.mdl，如图13-6所示，并用程序绘制系统的阶跃响应曲线。clear；[a，b，c，d]=linmod（sx2L1301b）；s1=ss（a，b，c，d）；sys=tf（s1）；step（sys），

程序运行后得到当K_p=28.312时对应着模型sx2L1301b.mdl绘制的系统单位阶跃响曲线，如图13-7所示，呈现发散的振荡，属于不稳定系统范畴。

图13-5 当K_p=28时系统阶跃响应

图13-6 调节器K_p=28.312时模型sx2L1301b.mdl(www.xing528.com)

8）以相角稳定裕度（γ=45°）为校正主要指标对系统进行滞后校正。

创建sx2L1301.mdl的开环模型sx2L1301op.mdl，如图13-8所示，即将模型sx2L1301.mdl反馈断开的开环状态。以下调用自编函数lagc.m的程序要用到它。

①利用开环模型sx2L1301op.mdl并调用自编函数lagc.m设计PI校正器。clear；[a，b，c，d]=linmod（sx2L1301op）；s1=ss（a，b，c，d）；s2=tf（s1）；gama=48；[Gc]=lagc（1，s2，[gama]），

程序运行后得到γ≥45°的校正器为G_c（s）。

图13-7 当K_p=28.312时系统阶跃响应

图13-8 系统开环模型sx2L1301op.mdl

②对以相角裕度为校正指标的校正器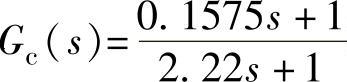验算设计的校正效果。

clear；[a，b，c，d]=linmod（sx2L1301op）；

s1=ss（a，b，c，d）；s2=tf（s1）；gama=48；

[Gc]=lagc（1，s2，[gama]），sys=s2∗Gc；margin（sys），

程序运行后绘制系统Bode图，如图13-9所示。从图中可见，校正后系统的相角稳定裕度γ=47.6°>45°，达到预期目的。

9）以剪切频率为校正主要指标（ω_c=40rad/s）对系统进行滞后校正。

①利用开环模型sx2L1301op.mdl并调用自编函数lagc.m设计PI校正器。

clear；[a，b，c，d]=linmod（sx2L1301op）；

s1=ss（a，b，c，d）；s2=tf（s1）；wc=40；[Gc]=lagc（2，s2，[wc]），

程序运行后得到ω_c≥40rad/s的PI校正器为。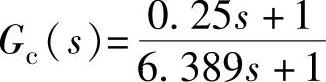

②验算设计的校正器的校正效果。

clear；[a，b，c，d]=linmod（sx2L1301op）；s1=ss（a，b，c，d）；s2=tf（s1）；

wc=40；[Gc]=lagc（2，s2，[wc]），sys=s2∗Gc；margin（sys），

程序运行后绘制系统Bode图，如图13-10所示。从图中可以看出，校正后系统的剪切频率ω_c=40.2rad/s>40rad/s，也达到预期目的。

图13-10 经校正器校正后的Bode图

10）用根轨迹校正器对系统进行滞后校正。

没有经过用根轨迹校正器对系统进行滞后校正前，系统模型为sx2L1301.mdl。利用该模型先绘制其单位阶跃响应曲线，以便与校正后的效果进行比较。

clear；[a，b，c，d]=linmod（sx2L1301）；s1=ss（a，b，c，d）；

sys=tf（s1）；t=0：0.001：0.3；step（sys，t），

程序运行后绘制系统单位阶跃响应曲线，如图13-11所示。单位阶跃响应呈现发散的振荡。

根据自动控制理论^[14]，给开环传递函数G（s）H（s）增加负极点的作用是使根轨迹向右

图13-9 经校正器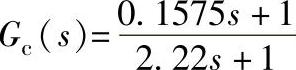校正后的Bode图

半S平面移动，其系统稳定性变差；而给开环传递函数G（s）H（s）增加负零点的作用是使根轨迹向左半S平面移动，其系统稳定性会变好。

在程序方式下（必须如此）运行以下MATLAB程序sx2L131.m，打开系统根轨迹设计器（见图13-12）与控制和估计工具管理器，按图中选择【Analysis】菜单中的【Response to Step Com-mand】命令，单击后即得到没有经过用根轨迹校正器校正的系统阶跃响应曲线（见图13-13），也是发散的振荡，与图13-11所示曲线一致。

%sx2L131.m

[a，b，c，d]=linmod（sx2L1301op）；

s1=ss（a，b，c，d）；s2=tf（s1）；rltool（s2），

图13-11 系统单位阶跃响应曲线

图13-12 被打开的系统根轨迹设计器

图13-13 根轨迹校正器中显示的发散振荡

在图13-14即控制与估计工具管理器中，选择【Compensator Editor】补偿校正器编辑器卡，单击“Add Pole/Zero”下的“Real Zero”为系统增加一个零点“-100”（见图13-14与图13-15），会使系统从不稳定变成稳定，且具有很好的性能指标。

图13-14 补偿校正器编辑器对话框

图13-15 设置零点“-100”后的编辑器

增加系统零点“-100”后，经存储且确认后，图13-12所示的系统根轨迹改变为图13-16。图13-13显示的发散振荡改变为图13-17。图中显示，其峰值时间t_p=0.01～0.02s，超调量σ%<30%，响应超调一、二次后，即回落到稳态值。这样的时域性能指标是非常理想的单位阶跃响应。

图13-16 增加零点“-100”后的根轨迹

图13-17 补偿校正后的系统单位阶跃响应

还可将图13-15中增加零点后的校正器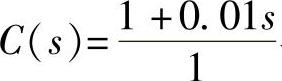与图13-3所示的动态结构图sx2L1301.mdl的前向通道串联得到模型sx2L1301rot.mdl，如图13-18所示，并运行以下程序，绘制的阶跃响应曲线（见图13-19）与图13-17一致，只是将横坐标缩短，使超调部分显示清楚。

clear；[a，b，c，d]=linmod（sx2L1301rot）；

s1=ss（a，b，c，d）；sys=tf（s1）；

t=0：0.001：0.06；step（sys，t），

图13-18 串联校正器的模型sx2L1301rot.mdl

图13-19 阶跃响应曲线