MATLAB实现控制系统稳定边界法的P、PI、PID校正设计

作者为控制系统稳定边界法P、PI、PID校正设计开发的自编函数是zn02.m，请看示例。

【例12-11】 已知过程控制系统被控对象传递函数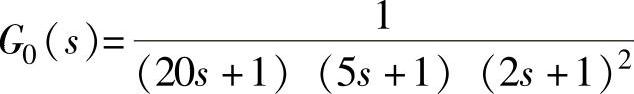，试用稳

定边界法计算串联调节器G_c（s）作P、PI、PID校正时的参数，并进行阶跃响应仿真。

解：程序方式下运行以下程序sx2X1211.m，程序中调用了自编函数zn02.m。

%MATLAB PROGRAM sx2L1211.m

clear；G1=tf（1，[201]）；G2=tf（1，[51]）；

d3=conv（[21]，[21]）；G3=tf（1，d3）；G=G1∗G2∗G3；p=3；

[Gc1，Kp1]=zn02（1，G，p），[Gc2，Kp2，Ti2]=zn02（2，G，p），

[Gc3，Kp3，Ti3，Td3]=zn02（3，G，p），

Gcc1=feedback（G∗Gc1，1）；step（Gcc1）；hold on；

Gcc2=feedback（G∗Gc2，1）；step（Gcc2）；Gcc3=feedback（G∗Gc3，1）；step（Gcc3）；

gtext（1 P control），gtext（2 PI control），gtext（3 PID control），

程序需在MATLAB命令窗口中运行，程序运行后有根轨迹图12-30，图上显示有十字光标，选择根轨迹与虚轴的交点用鼠标左键单击。再回到MATLAB命令窗口中，可以见到有计算出的根轨迹增益与极点值（应该力求准确定在根轨迹与虚轴的交点上，尽量使极点实部为0），还可见到字符“K”。应该在字符“K”后输入指令“return”，然后即可在MAT-LAB命令窗口中看到km=9.3797，wm=0.2422，这就是交点的系统增益K_m及其对应的振荡角频率ω_m。在MATLAB命令窗口中还看到用稳定边界法计算出P、PI、PID校正的参数。再弹出根轨迹图，再次用鼠标左键单击根轨迹与虚轴的交点，程序三次调用函数zn02.m，即这样操作三次，最后得到如图12-31所示的P、PI、PID三种校正时的阶跃给定响应曲线与校正器计算结果。

图12-30 系统闭环根轨迹图

图12-31　P、PI、PID校正后系统的阶跃响应曲线

以下是程序执行过程中在MATLAB命令窗口中留下的信息记录。

>>sx2X1211

Select a point in the graphics window

selected_point=

0.0012+0.2283i

km=8.6349

pole=

-0.6194+0.2407i

-0.6194-0.2407i

-0.0056+0.2335i(www.xing528.com)

-0.0056-0.2335i

K>>return

wm=0.2335

Gc=4.3174

Gc1=4.3174

Kp1=4.3174

Select a point in the graphics window

selected_point=

0.0012+0.2283i

km=8.6349

pole=

-0.6194+0.2407i

-0.6194-0.2407i

-0.0056+0.2335i

-0.0056-0.2335i

K>>return

wm=0.2335

Transfer function：

计算出三种P、PI、PID校正时校正器的参数分别为

①P校正器G_c1=K_p1=4.3174

②PI校正器K_p2=3.9289、T_i2=22.8748、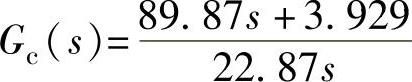

③PID校正器K_p3=5.586、T_i3=13.1253、T_d3=3.2813、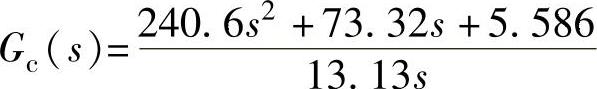

从图12-31所示稳定边界法计算的P、PI、PID校正阶跃给定响应曲线可以看到，P与PI校正的阶跃响应曲线上升的速度差不多快，PID校正的最快；三条曲线有两个不同的终了值。超调量都较大，以PI校正的为最大。