MATLAB实现最优控制校正设计（误差积分指标优化）

作者还为控制系统最优控制（误差积分指标最优）P、PI、PID校正设计开发了自编函数inmin01.m，请看示例。

【例12-10】 已知过程控制系统被控广义对象为一个带延迟的惯性环节，其传递函数为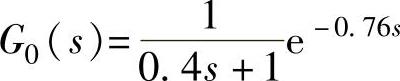，试用IAE、ISE、ITAE积分值最小准则计算P、PI、PID串联校正器的参数，并对其进行阶跃给定响应的仿真。

解：1）调用自编函数kttau.m计算带延迟惯性环节的三参数。

clear；n=1；d=[0.41]；G1=tf（n，d）；tau1=0.76；[np，dp]=pade（tau1，2）；

Gp=tf（np，dp）；G=G1∗Gp；[K，T，tau]=kttau（G），

程序运行后得到K=1、T=0.4、τ=0.7383。

2）计算比例（P）校正器并作阶跃响应仿真。

clear；K=1；T=0.4；tau=0.7383；[np，dp]=pade（tau，2）；

Gp=tf（np，dp）；G=tf（1，[0.41]）；iC=1：3；

for i=1：length（iC）

[Gc1，Kp]=inmin01（1，[K，T，tau，iC（i）]）

Gc=G∗Gc1；Gcc=feedback（Gc，Gp）；

set（Gcc，Td，tau）；

step（Gcc），hold on

end

gtext（IAE），gtext（ISE），gtext（ITAE），

程序运行后，可以得到三种最优控制下实现P校正时的参数：

①IAE积分最小准则校正器：G_c1=K_p=0.4932

②ISE积分最小准则校正器：G_c1=K_p=0.8061

③ITAE积分最小准则校正器：G_c1=K_p=0.4652

运行程序后还得到三种积分最小准则P校正的阶跃给定响应曲线如图12-27所示。三条曲线有三个不同的终了值，ITAE的最小，IAE的次之，ISE的最大。这可以从计算出的P校正器K_p的不同大小值看出。IAE与ITAE这两种的曲线接近重合，响应速度与超调都差不多。而ISE的响应速度最快，超调量也最大。

图12-27 积分最小准则P校正阶跃给定响应曲线

3）计算PI校正器并作阶跃响应仿真。

clear；K=1；T=0.4；tau=0.7383；[np，dp]=pade（tau，2）；Gp=tf（np，dp）；

G=tf（1，[0.41]）；iC=1：3；

for i=1：length（iC）

[Gc2，Kp，Ti]=inmin01（2，[K，T，tau，iC（i）]）

Gc=G∗Gc2；(www.xing528.com)

Gcc=feedback（Gc，Gp）；

set（Gcc，Td，tau）；

step（Gcc），hold on

end

gtext（IAE），gtext（ISE），gtext（ITAE），

程序运行后，可以得到三种最优控制下实现PI校正时的参数：

①IAE积分最小准则校正器K_p=0.5377、T_i=1.0147、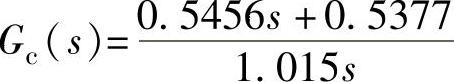

②ISE积分最小准则校正器K_p=0.7250、T_i=1.2788、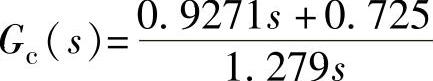

③ITAE积分最小准则校正器K_p=0.4720、T_i=0.9003、

运行程序后还得到三种积分最小准则PI校正如图12-28所示的阶跃给定响应曲线。三条曲线的终了值是一致的。IAE与ITAE这两种曲线接近重合，响应速度与过程相差不多。而ISE的响应速度较快，三种积分校正均没有超调，以ISE的振荡稍稍大一点。

图12-28 积分最小准则PI校正的阶跃响应曲线

4）计算PID校正器并作阶跃响应仿真。

clear；K=1；T=0.4；tau=0.7383；[np，dp]=pade（tau，2）；

Gp=tf（np，dp）；G=tf（1，[0.41]）；iC=1：3；

for i=1：length（iC）

[Gc3，Kp，Ti，Td]=inmin01（3，[K，T，tau，iC（i）]）

Gc=G∗Gc3；Gcc=feedback（Gc，Gp）；

set（Gcc，Td，tau）；

step（Gcc），hold on

end

gtext（IAE），gtext（ISE），gtext（ITAE），

程序运行后，可以得到三种最优控制下实现PID校正时的参数：

①IAE积分最小准则校正器：K_p=0.8160、T_i=0.7210、T_d=0.3870、

②ISE积分最小准则校正器：K_p=0.8377、T_i=0.5828、T_d=0.4150、

③ITAE积分最小准则校正器：K_p=0.7595、T_i=0.7468、T_d=0.2804、

运行程序后还得到三种积分最小准则PID校正如图12-29所示的阶跃给定响应曲线。三条曲线终了值是一致的。就响应速度而言，三条曲线差不多快；超调量以ITAE、IAE、ISE的顺序加大，ISE的超调量最大。而调节时间以ITAE的最短。

图12-29 积分最小准则PID校正的阶跃响应曲线