MATLAB实现Ziegler-Nichols控制系统整定公式校正设计

作者为控制系统Ziegler-Nichols整定公式P、PI、PID校正设计开发了自编函数zn01.m，请看示例。

【例12-8】 已知单回路控制系统控制对象为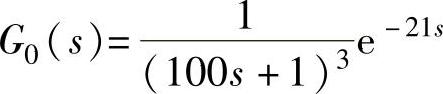，试用Ziegler-Nichols整定公式计算P、PI、PID串联校正器参数，并进行阶跃给定响应仿真。

解：

clear；G1=tf（1，[1001]）；G2=tf（1，[1001]）；G3=tf（1，[1001]）；

tau1=21；[np，dp]=pade（tau1，2）；Gp=tf（np，dp）；G=G1∗G2∗G3∗Gp；

[K，T，tau]=kttau（G）；[Gc1，Kp1]=zn01（1，[K，T，tau]）；

[Gc2，Kp2，Ti2]=zn01（2，[K，T，tau]）；

[Gc3，Kp3，Ti3，Td3]=zn01（3，[K，T，tau]）；

Gcc1=feedback（G1∗G2∗G3∗Gc1，Gp）；

set（Gcc1，Td，tau）；step（Gcc1）；hold on(https://www.xing528.com)

Gcc2=feedback（G1∗G2∗G3∗Gc2，Gp）；set（Gcc2，Td，tau）；step（Gcc2）；

Gcc3=feedback（G1∗G2∗G3∗Gc3，Gp）；set（Gcc3，Td，tau）；step（Gcc3）；

gtext（1 P control），gtext（2 PI control），gtext（3 PID control），

程序运行后得到P校正器为G_c（s）=2.8084

PI校正器为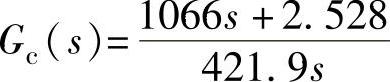

PID校正器为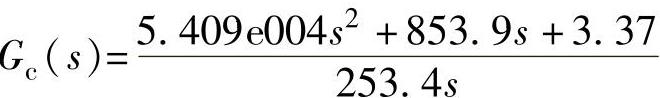

程序运行后，还绘制出系统的阶跃给定响应曲线如图12-25所示。由图可知，PID校正控制的效果最佳，超调既小，又快捷。

图12-25 校正后系统的阶跃给定响应曲线