MATLAB实现控制系统根轨迹滞后校正设计

作者也为根轨迹滞后校正设计开发了自编函数rlagc.m，请看示例。

【例12-7】 已知单位负反馈系统开环传递函数为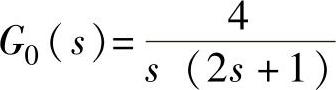，试用根轨迹法对系统进行滞后串联校正设计，1）使系统单位斜坡响应稳态误差e_ssv≤0.025v₀；2）阶跃响应超调量σ%≤12%；3）相角稳定裕度γ≥55°；4）阶跃响应调节时间t_s≤15s。

解：1）求校正器的放大系数K_c。根据自动控制理论，对Ⅰ型系统满足单位斜坡响应稳态误差e_ssv≤0.025v₀时，有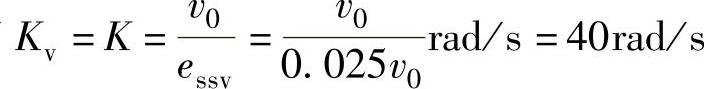，则校正器放大系数为。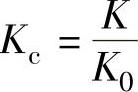

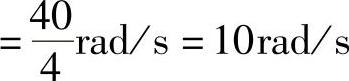2）校检原系统的阶跃响应超调量是否满足要求。

clear；K=40；n1=1；d1=conv（[10]，[21]）；

s1=tf（K∗n1，d1）；s2=[]；key=1；chec（key，s1，s2）；

程序运行后，可得到如图12-20所示的未经校正系统的Bode图及其性能指标，还有如图12-21所示的未校正系统的阶跃响应曲线。由图12-20可知系统的：

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=6.4° 剪切频率：ω_c=4.46rad/s

即系统的相角稳定裕度γ=6.4°<45°。由图12-21可以看到，未校正系统的阶跃响应超调量竟达80%，并有剧烈的振荡，故原系统需要校正。

图12-20 未校正系统Bode图

图12-21 未校正系统阶跃响应曲线

3）由期望极点位置确定校正器传递函数。为求校正器传递函数，参看图12-22a确定期望闭环主导极点s₁的位置。在图中直线s₁0与负实轴的夹角为α，则有ζ=cosα。

图12-22 二阶系统的闭环极点与根轨迹图

由σ%=12%用以下MATLAB程序将其转换成对应的ζ。

clear；sigma=0.12；zeta=sitoze（sigma）；

程序运行求得zeta=0.5594，取ζ=0.6。

用以下MATLAB程序绘制未校正系统的根轨迹图。(https://www.xing528.com)

clear；K=40；n1=1；d1=conv（[10]，[21]）；

s1=tf（K∗n1，d1）；rlocus（s1），

程序运行后得到未校正系统的根轨迹图如图12-22b所示。由图可以看出，根轨迹分离点d=-0.25。由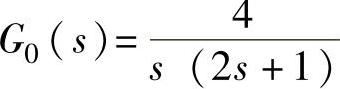可知未校正系统没有零点，有两个极点：p₁=0，p₂=-0.5。用以下程序确定由期望极点位置确定校正器传递函数。

clear；essv=0.025；x=-0.25；z1=0；p1=0；p2=0.5；zeta=0.6；

[Gc]=rlagc（essv，x，z1，p1，p2，zeta）；

程序运行后得校正器传递函数为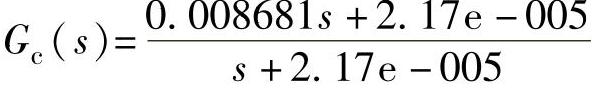，则校正系统传递函数为。

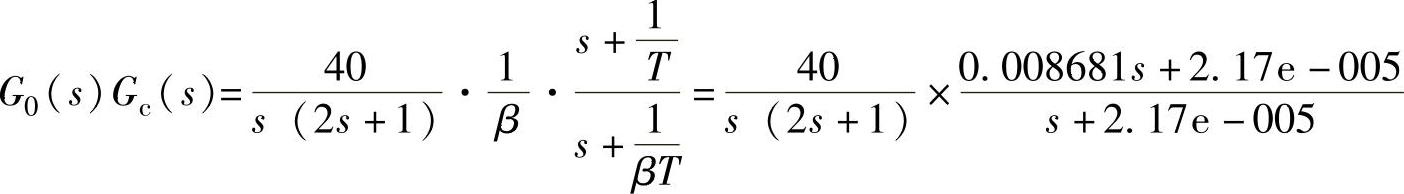4）校检校正器计算是否符合要求。

clear；K=40；n1=1；d1=conv（[10]，[21]）；

s1=tf（K∗n1，d1）；n2=[0.0086812.17e-005]；

d2=[12.17e-005]；s2=tf（n2，d2）；key=2；chec（key，s1，s2）；

程序运行后，可得到如图12-23所示的校正后系统的Bode图及其性能指标，还有如图12-24所示的未校正系统的阶跃响应曲线。由图12-23可知系统的：

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=58.7° 剪切频率：ω_c=0.298rad/s

图12-23 校正系统的Bode图

图12-24 校正后的阶跃响应曲线

相角稳定裕度γ=58.7°≥55°，已达到题目要求。由图12-24可看出系统超调量σ%=10.5445%<12%，已达到题目要求；峰值时间t_p=9.3718s；调节时间（5%）t_s=12.7798s<15s也已达到要求。