MATLAB实现控制系统根轨迹超前校正设计

控制系统根轨迹设计是与Bode图设计并列的第2类设计法。作者为根轨迹超前校正设计开发了自编函数rtloc.m，请看示例。

【例12-6】 已知单位负反馈系统的开环传递函数为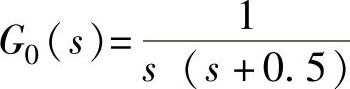，试用根轨迹解析方法对系统进行超前串联校正设计，使系统闭环主导极点的阻尼比ζ=0.5，自然振荡角频率ω_n=5rad/s，静态速度误差系数K_v=20rad/s，系统相角稳定裕度γ≥40°。

解：1）求满足系统静态速度误差要求的校正器的放大系数K_c。

已知单位负反馈系统为Ⅰ型系统，故满足系统静态速度误差要求的放大系数应为K=Kv=20rad/s，校正器的放大系数。

2）作原系统的Bode图与阶跃响应曲线，检查是否满足题目要求。clear；n1=1；d1=conv（[10]，[10.5]）；

s1=tf（n1，d1）；s2=[]；key=1；chec（key，s1，s2）；

程序运行后，可得到如图12-16所示未经校正系统的Bode图及其性能指标，还有如图12-17所示的未校正系统的阶跃响应曲线。由图12-16可知系统的：

模稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=28° 剪切频率：ω_c=0.94rad/s

即系统的相角稳定裕度γ=28°<40°。由图12-17可以看到，未校正系统的阶跃响应超调量竟达44.6656%，故原系统需要校正。

图12-16 未经校正系统的Bode图及其性能指标

图12-17 未校正系统的阶跃响应曲线

3）根据使系统满足的闭环主导极点用根轨迹解析方法计算超前校正器传递函数。

由闭环主导极点阻尼比ζ=0.5，自然振荡角频率ω_n=5rad/s，即有闭环主导极点

clear；zeta=0.5；wn=5；

s1=-zeta∗wn+j∗wn∗sqrt（1-zeta^2），

程序运行后得到

s1=-2.5000+4.3301i(www.xing528.com)

根据系统闭环特征根s₁，2与校正器放大系数K_c=20rad/s计算校正器传递函数。

clear；s1=-2.5+4.3301i；kc=20；

n1=1；d1=[10.50]；sope=tf（n1，d1）；

[Gc]=rtloc（2，sope，[s1，kc]）；

程序运行后得到超前校正器传递函数。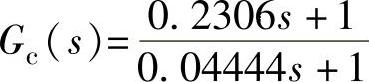

4）检查校正后系统是否满足题目要求。

clear；K=20；n1=1；d1=[10.50]；s1=tf（K∗n1，d1）；

n2=[0.23061]；d2=[0.044441]；s2=tf（n2，d2）；

key=2；chec（key，s1，s2）；

程序运行后，可得到如图12-18所示的校正后系统的Bode图及其性能指标，还有如图12-19所示的校正后系统的阶跃响应曲线。由图12-18可知系统的：

模稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=43.4° 剪切频率：ω_c=5.63rad/s

即系统相角稳定裕度：γ=43.4°>40°。系统自然振荡角频率ω_n=5rad/s、系统阻尼比ζ=0.5。由图12-19可以看到，校正后系统阶跃响应超调量σ%由44.6656%减少为32.8719%，故系统满足校正要求。

已经说明过，校正后系统剪切频率从ω_c=0.94rad/s增大到5.63rad/s，稳定裕度从γ=28°提高到43.4°，超调量减小，这既看到超前校正的作用，也说明根轨迹解析方法对系统进行超前串联校正设计自编函数的有效。

图12-18 校正后系统Bode图

图12-19 校正后系统阶跃响应曲线