MATLAB实现控制系统Bode图常规设计法滞后校正设计

控制系统Bode图滞后校正也是校正设计最基本的设计方法，作者也为此开发了自编函数lagc.m，请看示例。

【例12-4】 已知单位负反馈系统的开环传递函数为，式中K₀=2rad/s。系统额定转速为35r/min，输出角度误差e_ss（∞）=3°。1）试用Bode图设计方法对系统进行串联滞后校正设计，使之满足校正后的相角裕度γ≥45°；2）对校正补偿器进行有源网络实现的参数计算。

解：1）系统稳态性能指标计算。

本题给定系统为Ⅰ型，系统在匀速信号作用下稳态误差为常值，那么，满足系统稳态性能指标要求的系统开环放大系数为

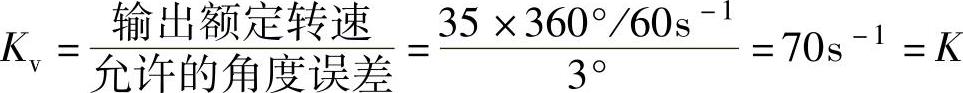
根据自动控制理论与题意，则校正环节要求的放大系数为，则满足稳态性能指标要求的系统开环传递函数为。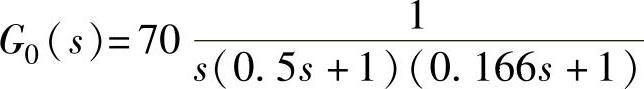

2）作原系统的Bode图与阶跃响应曲线，检查是否满足要求。

clear；K=70；n1=1；d1=conv（conv（[10]，[0.51]），[0.1661]）；

s1=tf（K∗n1，d1）；s2=[]；key=1；chec（key，s1，s2）；

程序运行后得到未校正系统Bode图如图12-5所示，还有如图12-6所示的未校正系统阶跃响应曲线。由图12-5可知未校正系统的频域性能指标：

幅值稳定裕度：L_h=-18.8dB -π穿越频率：ω_g=3.47rad/s

相角稳定裕度：γ=-42.7° 剪切频率：ω_c=8.78rad/s

由计算的相角稳定裕量与模稳定裕量均为负值可知，这样的系统根本不能工作。这也可从图12-6看到阶跃响应曲线为发散的振荡，故系统必须校正。

图12-5 未校正系统Bode图与频域性能

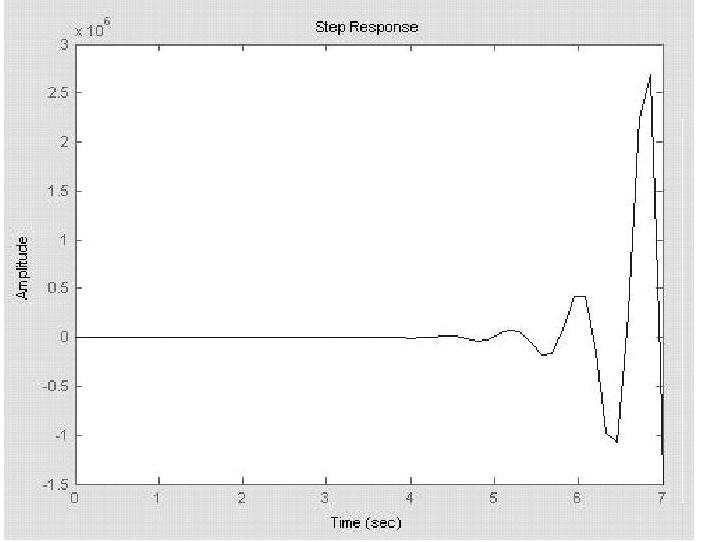
图12-6 未校正系统的单位阶跃响应曲线

3）计算校正后系统剪切频率的上限。根据题意，校正后系统相角裕度γ≥45°。先不考虑校正环节的相频特性，根据自动控制原理，在剪切频率处，有γ=φ（ω_c）-（-180°），即

45°=180°-90°-arctan（0.5ω_c）-arctan（0.166ω_c）

解此三角方程，求出满足系统的相角裕度γ≥45°的剪切频率的上限：

clear；syms omegac；

[omegac]=solve（atan（0.5∗omegac）+atan（0.166∗omegac）=（45）∗pi/180）；

omegac=vpa（omegac，3），

程序运行后得到系统剪切频率上限ω_c=1.29rad/s，必须有ω_c≤1.29rad/s。取校正后系统剪切频率ω_c2=1.2rad/s。

4）求滞后校正器的传递函数。取校正后系统剪切频率ω_c2=1.2rad/s与相角裕度γ=45°。如果已知系统校正后相角裕度与剪切频率，可以调用以下函数lagc（）的程序求滞后校正补偿器的两个传递函数。

clear；K=70；n1=1；d1=conv（conv（[10]，[0.51]），[0.1661]）；

sope=tf（K∗n1，d1）；wc=1.2；gama=46；

[Gc]=lagc（2，sope，[wc]），[Gc]=lagc（1，sope，[gama]），

程序运行后得到按ω_c2=1.2rad/s滞后校正补偿器传递函数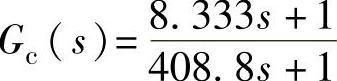、按γ=45°的滞后校正补偿器传递函数。程序校正后得到ω_c2=1.2rad/s的Bode图和阶跃响应分别如图12-7和图12-8所示。

图12-7 校正后ω_c2=1.2rad/s的Bode图

图12-8　ω_c2=1.2rad/s的阶跃响应

5）校验系统校正后频域性能是否满足题目要求。

①当剪切频率ω_c2=1.2rad/s时有校正器的系统传递函数为

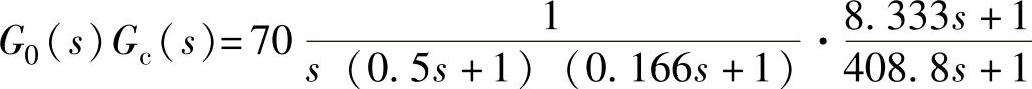
clear；K=70；n1=1；d1=conv（conv（[10]，[0.51]），[0.1661]）；s1=tf（K∗n1，d1）；

n2=[8.3331]；d2=[408.81]；s2=tf（n2，d2）；key=2；chec（key，s1，s2）；

程序运行后得到

幅值稳定裕度：L_h=14.3dB -π穿越频率：ω_g=3.33rad/s

相角稳定裕度：γ=42.1° 剪切频率：ω_c=1.2rad/s

由数据可以看出，系统校正后相角稳定裕度γ=42.1°<45°，没满足题目要求。再按相角裕度γ=45°的校正器进行校核。

②当相角裕度γ=45°时有校正器的系统传递函数为

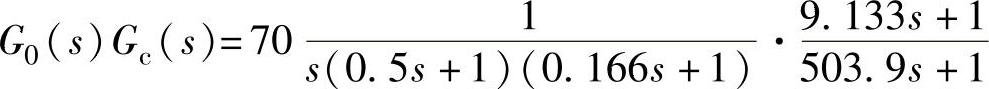
clear；K=70；n1=1；d1=conv（conv（[10]，[0.51]），[0.1661]）；

s1=tf（K∗n1，d1）；n2=[9.1331]；d2=[503.91]；s2=tf（n2，d2）；

key=2；chec（key，s1，s2）；

程序运行后得到校正后系统Bode图如图12-9所示。由图可知系统的：

幅值稳定裕度：L_h=15.4dB -π穿越频率：ω_g=3.34rad/s

相角稳定裕度：γ=45.3° 剪切频率：ω_c=1.1rad/s

数据显示，校正后系统相角稳定裕度γ=45.3°>45°，剪切频率ω_c=1.1rad/s<1.29rad/s。本来滞后校正就是以牺牲系统快速性来换取稳定裕度的，所以指标完全满足题目要求。

③程序还绘制出校正后阶跃响应曲线如图12-10所示，并计算了系统性能指标：超调量σ%=27.1863%；峰值时间t_p=2.5956s；调节时间（5%）t_s=4.2179s。

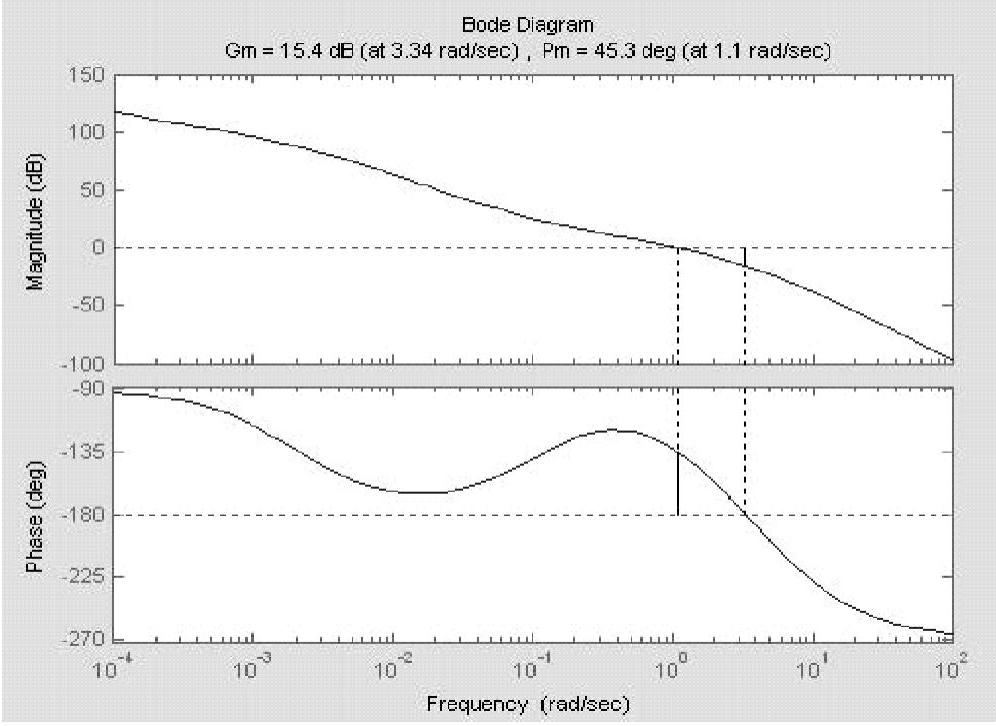
图12-9 按γ=45°校正后系统Bode图

图12-10 校正后的单位阶跃响应曲线

由以上数据看到，校正后系统剪切频率从ω_c=8.78rad/s减少到1.1rad/s，稳定裕度从γ=-42.7°提高到45.3°，系统从不稳定到稳定，这正是滞后校正的功能所在。

6）对校正补偿器进行有源网络实现的参数计算。根据校正环节K_c=35，G_c（s）=35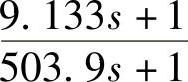。选择同相输入PI有源校正网络如图12-11所示。对图12-11所示的传递函数推导如下。(www.xing528.com)

根据模拟电子技术理论：①为保持两个输入端对地电阻相等，有R₀=R₁//R₂；②反相输入端Σ与同相输入端Σ′是虚短路，即U_i=U_Σ=U_Σ′；③有分压表达式：

即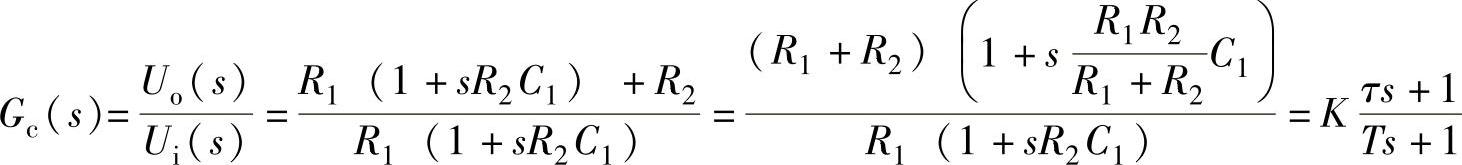

式中，

图12-11 近似PI有源校正网络

请注意，，，T=R₂C₁这三个方程，实际上只有两个是独立的，即三个参数R₁，R₂，C只有两个是独立的，第3个必须根据工程实际进行选取。

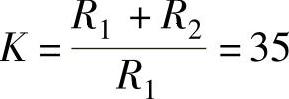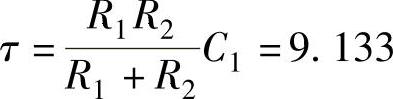为实现，需确定参数。按以上公式带入数据：，，T=R₂C₁=503.9。选C₁=10×10^-6F

clear；syms R0 R1 R2 C1；

[R1，R2]=solve（503.9=R2∗10^（-5），R1∗R2/（R1+R2）∗10^（-5）=9.133）；

R1=vpa（R1，6），R2=vpa（R2，6），

程序运行结果

R1=930159.

R2=.503900e8

还有

clear；R1=930159.；R2=.503900e8；

[R0]=solve（1/R0=1/930159.+1/.503900e8）；

R0=vpa（R0，6），

程序运行结果

R0=913300.

即R₀=913300Ω，R₁=930159Ω，R₂=50390000Ω，还选有C=1×10^-6F。

根据以上数据，要按元件标称值选择电阻、电容。在进行工程实践时，电阻R₂与R₃通常要使用电位器以便调试确定电阻值。电位器同样要按其系列标称值进行选择。

【例12-5】 已知单位负反馈系统的开环传递函数为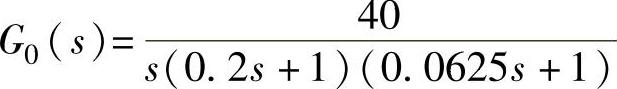，试用Bode图设计方法对系统进行串联滞后—超前校正设计，使之满足校正后的系统开环增益不变，相角裕度γ≥60°，超调量σ%<10%；调节时间（5%误差带）t_s<0.5s。

解：1）作原系统的Bode图与阶跃响应曲线检查是否满足题目要求。

clear；K=40；n1=1；d1=conv（conv（[10]，[0.21]），[0.06251]）；

s1=tf（K∗n1，d1）；s2=[]；key=1；chec（key，s1，s2）；

程序运行后，可得未校正系统的Bode图与频域性能如图12-12所示，还有如图12-13所示的未校正系统阶跃响应曲线。由图12-13可知未校正系统的频域性能指标：

幅值稳定裕度：L_h=-5.6dB -π穿越频率：ω_g=8.94rad/s

相角稳定裕度：γ=-14.8° 剪切频率：ω_c=12.1rad/s

计算数据表明，相角稳定裕量与模稳定裕量均为负值，这样的系统是根本不能工作的。这也可从发散振荡的阶跃响应曲线（见图12-13）看到，系统必须校正。

图12-12 未校正系统的Bode图

图12-13 未校正系统的阶跃响应曲线

2）用试探法选γ=40°先求滞后校正器的传递函数。

clear；K=40；n1=1；d1=conv（conv（[10]，[0.21]），[0.06251]）；

sope=tf（K∗n1，d1）；gama=40；[Gc]=lagc（1，sope，[gama]），

程序运行得到滞后校正器。

3）将G_c1（s）与原对象合并作新对象再用试探法选γ=40°求超前校正器。

clear；K=40；n1=1；d1=conv（conv（[10]，[0.21]），[0.06251]）；

s1=tf（K∗n1，d1）；n2=[3.0371]；d2=[30.171]；s2=tf（n2，d2）；

sope=s1∗s2；gama=40；[Gc]=leadc（1，sope，[gama]）；

程序运行后得到超前校正器。

4）对滞后—超前校正器校验系统校正后系统性能是否满足题目要求。

clear；K=40；n1=1；d1=conv（conv（[10]，[0.21]），[0.06251]）；

s1=tf（K∗n1，d1）；n21=[3.0371]；d21=[30.171]；s21=tf（n21，d21）；

n22=[0.4091]；d22=[0.070171]；s22=tf（n22，d22）；

s2=s21∗s22；key=2；chec（key，s1，s2）；

程序运行后得到校正后系统Bode图如图12-14所示。由图可知系统的：

幅值稳定裕度：L_h=13.8dB -π穿越频率：ω_g=17.1rad/s

相角稳定裕度：γ=62.1° 剪切频率：ω_c=5.9rad/s

由数据看出，系统校正后相角稳定裕度γ=62.1°>60°。程序还绘制出校正后阶跃响应曲线如图12-15所示，其超调量σ%=5.639%<10%，调节时间（5%误差带）t_s=0.449s<0.5s。所以指标完全满足题目要求。

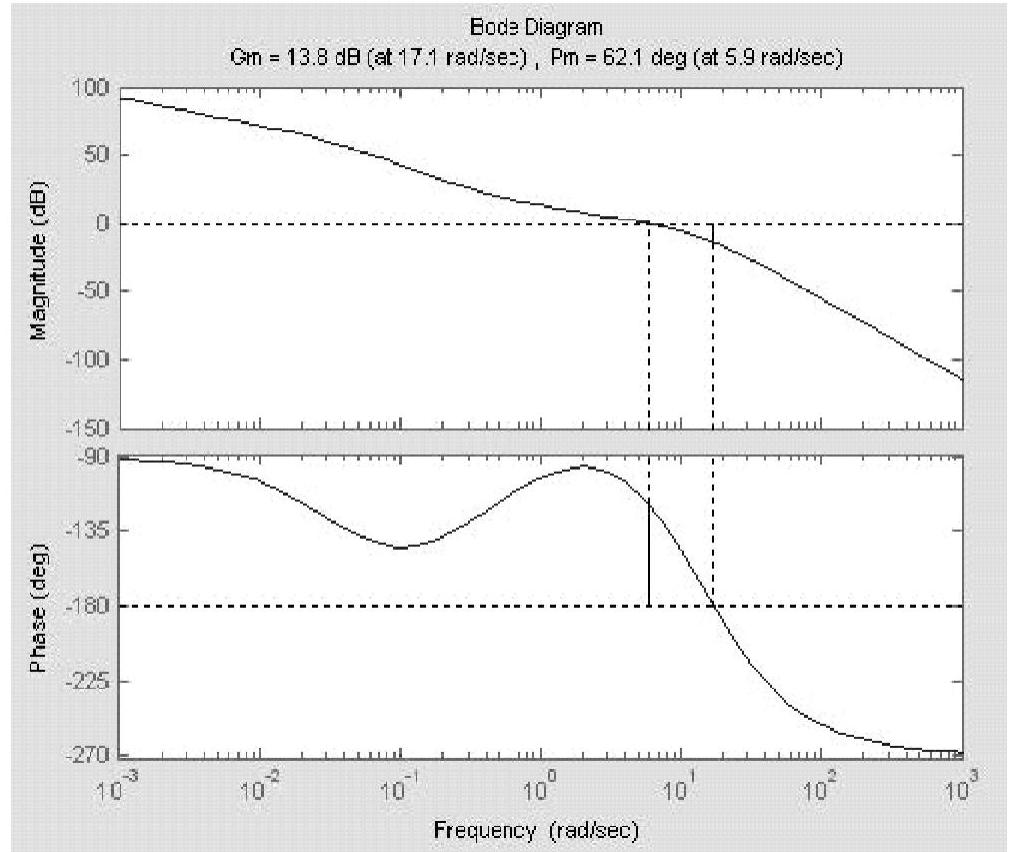
图12-14 校正后系统Bode图

图12-15 校正后阶跃响应曲线