MATLAB实现超前校正设计控制系统Bode图常规设计法

控制系统Bode图超前校正常规设计法是最基本的设计方法，自编函数leadc.m就是为此开发的。请看示例。

【例12-3】 已知单位负反馈系统被控对象传递函数为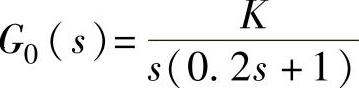，试用Bode图设计方法对系统进行超前串联校正设计，使系统校正后满足：①在单位速度信号下的K_v=50rad/s²；②γ≥40°；③ω_c≥20rad/s；④σ%≤28%。

解：1）求满足稳态误差要求的系统开环增益K。根据自动控制理论与题意，本题给定系统为Ⅰ型，速度误差系数K_v=K，系统的开环增益K=K_v=50rad/s²。

2）检查原系统是否满足题目要求。

clear；K=50；n1=1；d1=conv（[10]，[0.21]）；

s1=tf（K∗n1，d1）；s2=[]；key=1；chec（key，s1，s2）；

再次提醒，chec.m中有暂停函数pause，需按下任意键显示两图。程序运行后，可得未校正系统的Bode图如图12-1所示，还有如图12-2所示的未校正系统阶跃响应曲线。由图12-1可知：

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=18° 剪切频率：ω_c=15.4rad/s

其中相角稳定裕度γ=18°<40°，剪切频率ω_c=15.4rad/s<20rad/s。这都不满足题目的要求。从图12-2可以看到系统阶跃响应超调量σ%>60%，系统必须校正。

3）根据γ≥40°，选择γ=50°、ω_c=20rad/s，计算超前校正器传递函数。

clear；K=50；n1=1；d1=conv（[10]，[0.21]）；

sope=tf（K∗n1，d1）；vars（1）=50；vars（2）=20；gama0=18；c1=6；c2=18；

[Gc]=leadc（3，sope，vars，gama0，c1，c2）；

程序运行后得到超前串联校正器传递函数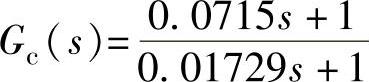。(www.xing528.com)

图12-1 未校正系统的Bode图

图12-2 未校正系统的阶跃响应曲线

4）校验校正后系统性能是否满足题目要求。

clear；K=50；n1=1；d1=conv（[10]，[0.21]）；s1=tf（K∗n1，d1）；

n2=[0.07151]；d2=[0.017291]；s2=tf（n2，d2）；key=2；chec（key，s1，s2）；

程序运行后得到校正后系统的Bode图如图12-3所示，还有如图12-4所示的系统阶跃响应曲线。由图12-3可知系统频域性能指标：

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=50° 剪切频率：ω_c=20rad/s

看到校正后系统剪切频率ω_c=20rad/s、γ=50°≥40°，已满足要求。从图12-4也看到

σ%=22.6172%<28%，即也满足要求。

由以上数据看到，校正后系统剪切频率增大，稳定裕度提高，超调量减小，这正是超前校正的功能所在。

图12-3 校正后系统Bode图

图12-4 校正后系统阶跃响应曲线