系统校正动态性能指标要求解析

大体上也有两种情况：一是已知系统的频域性能指标，如系统校正后剪切频率ω_c或相角稳定裕度γ，这两个指标直接用于校正器设计；二是已知系统时域性能指标，如系统校正后超调量σ%或调节时间t_s。在已知系统传递函数或系统型别时，根据自动控制理论，有以下关系式将频域指标与时域指标两者联系起来：

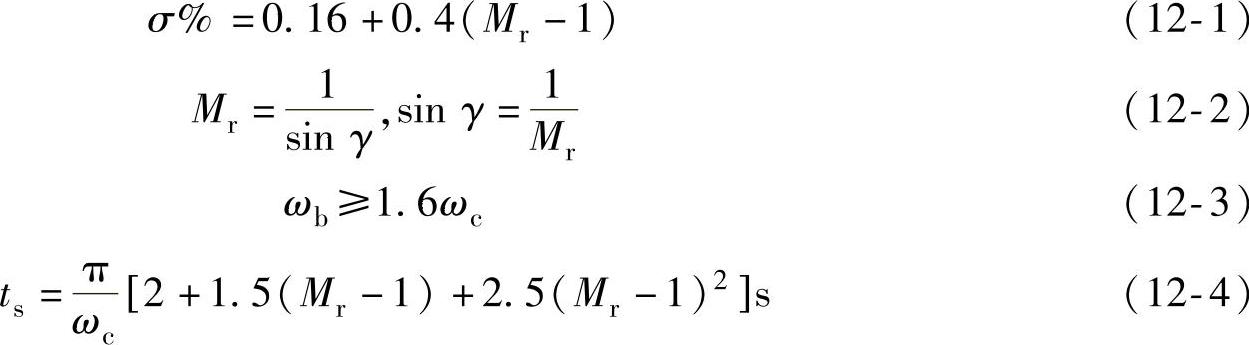
根据以上几个关系式，即由σ%算出M_r，再由M_r算出γ；由M_r与t_s算出ω_c。作者编制了两个函数sitoga.m与tstoom.m（参见附录B）来求解以上两个问题。系统超调量σ%与其对应相角稳定裕度γ之间有一定的相关关系。请看以下示例。

【例12-1】 若系统超调量从σ%=10%按10%递增至80%，求这些超调量对应的系统相角稳定裕度γ，并用自编函数gatosi.m来验算。

解：1）用以下MATLAB程序求解。

clear；sigma=[0.2，0.3，0.4，0.5，0.6，0.7，0.8]；

for i=1：length（sigma）

[gama]=sitoga（sigma（i））；

end

将程序运行结果列成表12-1。

表12-1 系统超调量与其超调量间的关系

从表12-1所示的数据可以看出，系统的超调量越小，则系统的相角稳定裕度越大；也可以是系统的相角稳定裕度越大，那么系统的超调量越小。反之亦然。

2）对表12-1所示部分数据运行调用自编函数gatosi.m的程序来验算。

clear；gama=[65.4，47.8，38.7，32.7]；

for i=1：length（gama）(www.xing528.com)

[sigma]=gatosi（gama（i））；

end

程序运算后的数据说明自编函数sitoga.m、gatosi.m计算正确、有效。读者可自行验算其他数据。

在系统超调量σ%一定的情况下，系统调节时间与其对应的系统剪切频率ω_c之间也有一定的相关关系。请看下例。

【例12-2】 若系统的超调量σ%=20%，而调节时间从t_s=0.1s至t_s=0.8s，试用自编函数tstoom.m计算这个超调量与调节时间对应的系统剪切频率ω_c。

解：用以下MATLAB程序求解。

clear；sigma=0.20；ts=[0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8]；

for i=1：length（ts）

[omegac]=tstoom（sigma，ts（i））；

end

将程序运行结果列成表12-2。

表12-2 系统σ%=20%时调节时间t_s与其剪切频率ω_c间的关系

从表12-2所示的数据可以看出，系统超调量不变（σ%=28%）时，系统调节时间越短，则要求系统剪切频率ω_c越大；也就是若系统剪切频率间ω_c越大，则系统调节时间就越短。反之亦然。