MATLAB实现离散系统动态性能分析的案例分析

《控制系统MATLAB计算及仿真》在连续系统的MATLAB计算与仿真部分对离散系统的MATLAB函数命令已一并作了介绍。以上多个示例中已经涉及离散系统动态性能分析。在此，就离散系统动态性能分析的MATLAB实现再举例。

【例11-20】 一离散系统如图11-5所示。图中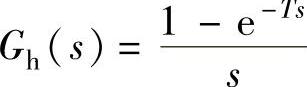为零阶保持器，线性部分的传递函数为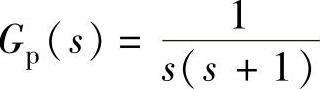，T=0.25s。1）计算系统开环与闭环的脉冲传递函数G（z）、Φ（z）；2）计算当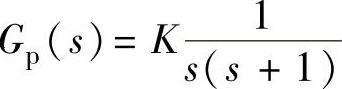时使系统稳定的K值范围；3）计算当输入信号r（t）=1（t）、r（t）=t与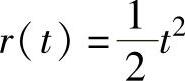时系统的稳态误差；4）根据w平面的系统开环脉冲传递函数G（w）绘制系统Bode图并求频域性能指标；5）根据T=0.25s时G（z）绘制负反馈闭环系统阶跃响应曲线；6）计算当r（t）=1（t）时系统输出响应c^∗（t）。

解：1）计算系统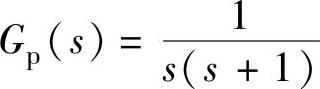，T=0.25s时脉冲传递函数G（z）、Φ（z）。

clear；num=[1]；den=[110]；T=0.25；

key=2；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到T=0.25s时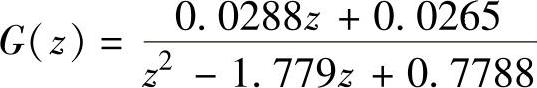

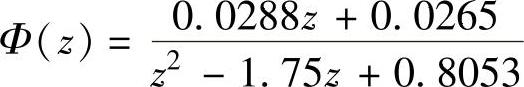
2）计算系统稳定时K的取值范围。

①再次写出系统开环脉冲传递函数。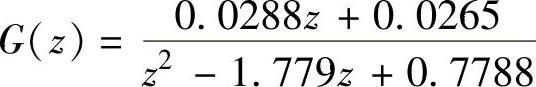

②考虑系数K后得到。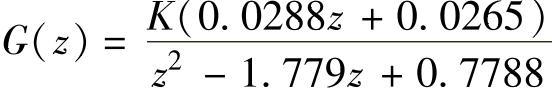

③用符号计算法求w变换后的闭环特征方程D（w）=0。

clear；syms w z K；Dzn=K∗（0.0288∗z+0.0265）；

Dzd=z^2-1.779∗z+0.7788；key=1；[Dw，Gw]=Dzw（key，Dzn，Dzd）；

程序运行后得到

D（w）=（0.0553∗K-0.0002）w²+（0.4424-0.053K）w+（3.5578-0.0023K）=0

④应用Lienard-Chipard稳定判据，系统稳定的必要充分条件是：特征方程的各项系数

均大于0，即a₀>0、a₁>0、a₂>0、D₁=a₁>0，那么有

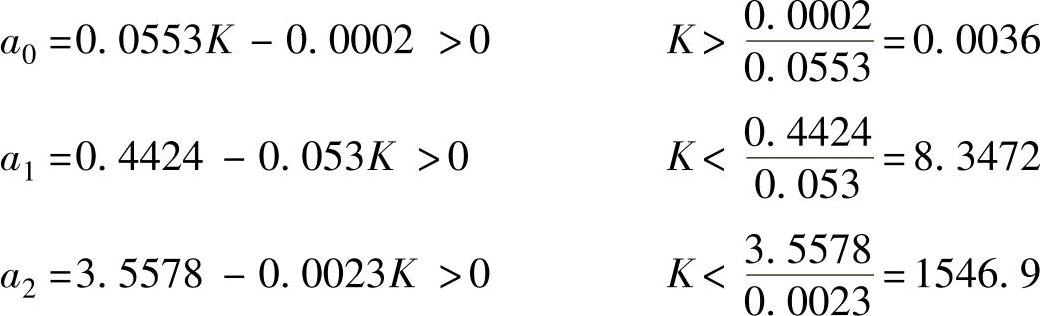
取0.0036<K<8.3472

3）计算当输入信号r（t）=1（t）、r（t）=t与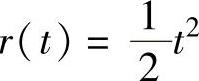时系统的稳态误差。

clear；syms z；Gz=（0.0288∗z+0.0265）/（z-1）/（z-0.7788）；

T=0.25；[Kp，Kv，Ka，ep，ev，ea]=Kpvaz（Gz，T）；

程序运行后得到K_p=∞、e_ssp=0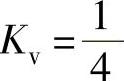；、essv=1；Ka=0、essa=∞。

4）根据w平面的系统开环脉冲传递函数G（w）绘制系统Bode图并求频域性能指标。

①取双线性变换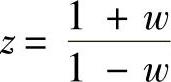计算w平面的系统开环脉冲传递函数G（w）。

clear；syms w z K；Dzn=0.0288∗z+0.0265；；

Dzd=z^2-1.779∗z+0.7788；key=2；[Dw，Gw]=Dzw（key，Dzn，Dzd）；

程序运行后得到

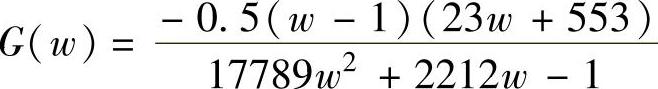
②根据w平面的系统开环脉冲传递函数G（w）绘制系统Bode图并求频域性能指标。

clear；n=conv（[-0.50.5]，[23553]）；d=[177892212-1]；

Gw=tf（n，d）；w=logspace（-3，3）；margin（Gw）；

程序运行后绘制Bode图，如图11-16所示，程序运行后还计算得到：

幅值裕度G_m即L_h=18.4dB -π穿越频率ω_cg即ω_g=0.361rad/s

相角稳定裕度P_m即γ=46.1° 剪切频率ω_cp即ω_c=0.0983rad/s

这些频域性能指标说明系统不仅稳定，而且频域性能已满足一般要求。

5）根据T=0.25s时G（z）绘制负反馈闭环系统阶跃响应曲线。(www.xing528.com)

clear；T=0.25；t=0：0.25：20；

s1=tf（[0.0288，0.0265]，[1，-1.7788，0.7788]，T）；

sys=feedback（s1，1）；step（sys，t）；grid；

程序运行后绘制负反馈闭环系统阶跃响应曲线，如图11-17所示。

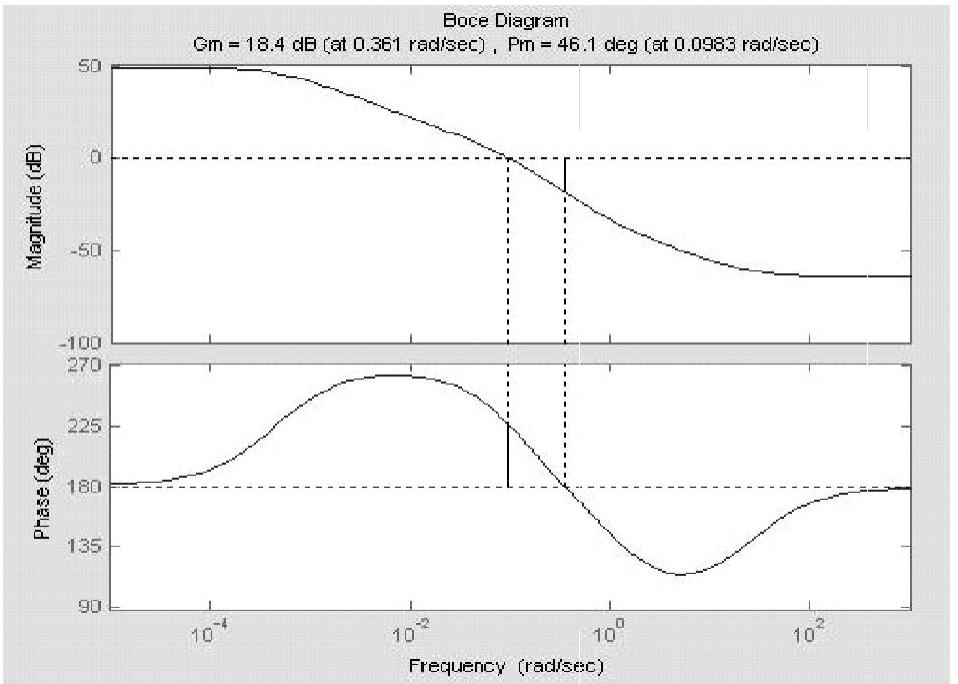
图11-16 系统Bode图

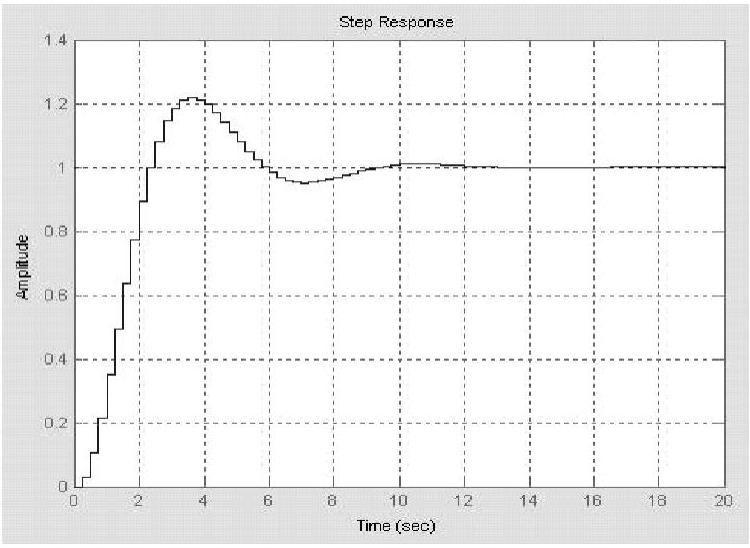
图11-17 负反馈闭环系统阶跃响应曲线

6）用MATLAB符号计算法计算r（t）=1（t）时的系统输出响应c^∗（t）。

clear；syms z；Rz=z/（z-1）；N=8；

phiz=（0.0288∗z+0.0265）/（z^2-1.75∗z+0.8053）；

[cn]=phiRz（phiz，Rz，N）；

程序运行后得到

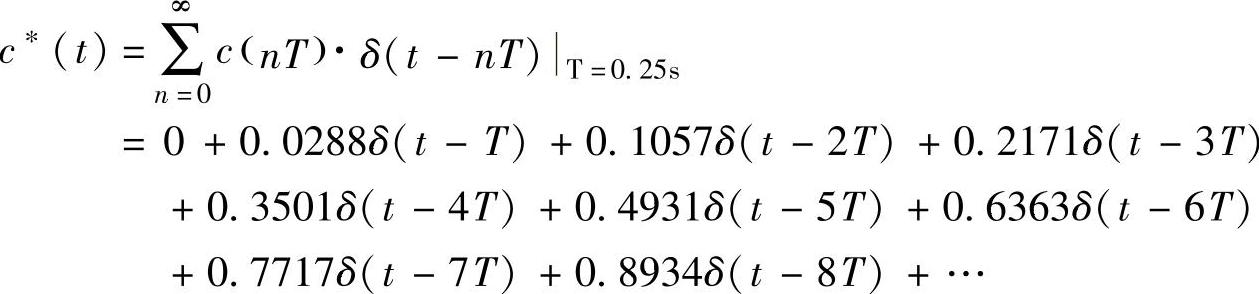
【例11-21】已知采样系统开环传递函数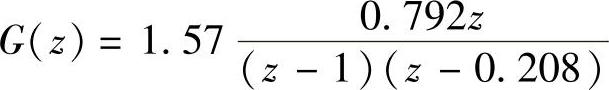，1）试绘制采样系统的Nyquist图并判稳；2）试绘制系统的Bode图并判稳。

解：1）试绘制采样系统的Nyquist图并判稳。

①取线性代换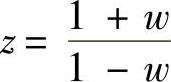，求w域的开环脉冲传递函数G（w）。

clear；syms w z K；Dzn=1.57∗0.792∗z；；

Dzd=（z-1）∗（z-0.208）；key=2；[Dw，Gw]=Dzw（key，Dzn，Dzd）；

程序运行后得到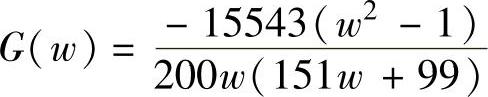

②绘制采样系统的Nyquist图并判稳。

clear；n=[-15543/200015543/200]；

d=[151990]；sys=tf（n，d）；nyquist（sys），

程序运行后绘制系统Nyquist图，如图11-18所示。根据Nyquist稳定判据，Nyquist曲线不包围（-1，j0）点，所以系统闭环稳定。

2）试绘制系统的Bode图并判稳。

clear；n=[-15543/200015543/200]；

d=[151990]；sys=tf（n，d）；margin（sys），grid；

程序运行后绘制Bode图，如图11-19所示，程序运行后还计算得到

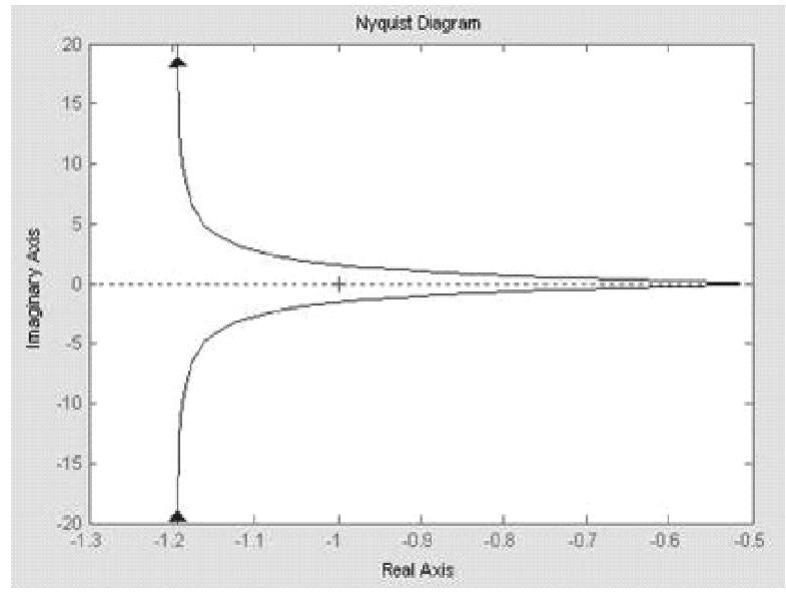
图11-18 采样系统Nyquist图

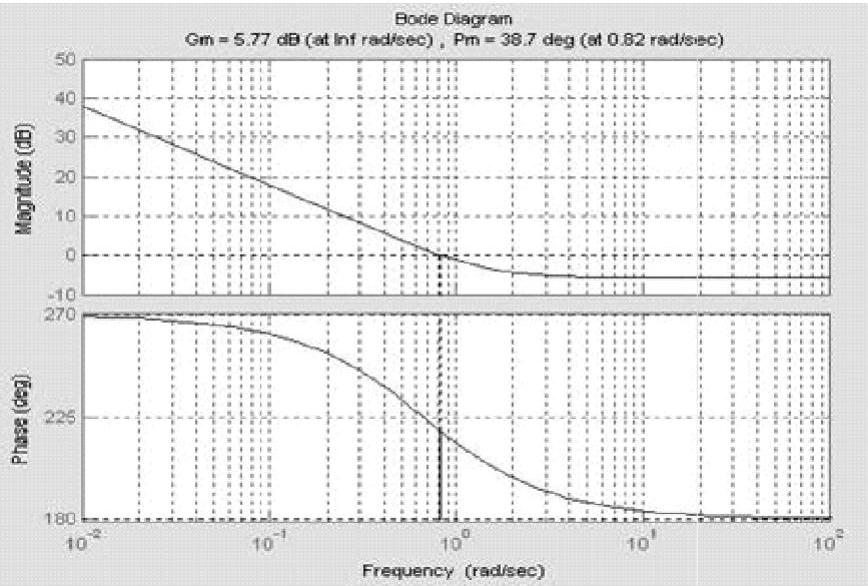
图11-19 系统Bode图

幅值裕度G_m即L_h=5.77dB -π穿越频率ω_cg即ω_g=∞rad/s

相角稳定裕度P_m即γ=38.7° 剪切频率ω_cp即ω_c=0.82rad/s

这些频域性能指标说明系统不仅稳定（与Nyquist判据判稳结论一致），而且频域性能已满足一般要求。