MATLAB实现离散系统稳定性分析

有关离散系统稳定性分析稍微要麻烦点，以上示例中已有涉及。连续线性系统的稳定性分析是基于系统闭环特征根在s平面中的位置，若全在虚轴之左，则系统稳定。那么要在z平面上研究离散系统的稳定性，则要明确s平面与z平面间的对应关系，这就是从s平面到z平面的映射。根据自动控制原理，当位于s左半平面的点，对应于z平面上单位圆之内；反之，位于s右半平面的点，对应于z平面上单位圆之外。再将z平面映射到w平面，则将特征方程D（z）=0转换为D（w）=0之后，便可应用连续系统的稳定判据。

【例11-16】 已知系统特征方程为D（z）=3z³+3z²+2z+1=0，试在w平面用代数稳定判据判别该系统的稳定性。

解：取代换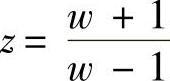代入特征方程，得

clear；syms z w D Dw；z=（w+1）/（w-1）；D=3∗z^3+3∗z^2+2∗z+1；[n，d]=numden（D），Dw=n/d，

程序执行结果D（w）=（9w³+7w²+7w+1）/（w-1）3=0，取分式分子为0，那么有(www.xing528.com)

9w³+7w²+7w+1=0

应用连续系统的Lienard-Chipard稳定判据，系统稳定的必要充分条件是：特征方程的各项系数均大于0，且Hurwitz行列式中奇数阶子行列式（即D₁、D₃、D₅、…）或偶数阶子行列式（即D₂、D₄、D₆、…）大于0。

现特征方程式中各项系数均大于零，特征方程最高阶n=3，取偶数阶即2阶子行列式

故离散系统稳定。