离散系统时域响应的MATLAB实现

离散系统时域响应的MATLAB实现显然要使用程序完成。再次提请读者，要特别关注MATLAB符号计算与MATLAB函数计算的不同使用与配合使用。

【例11-14】 一离散系统如图11-5所示。图中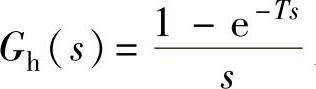为零阶保持器，T=1s。线性部分的传递函数为。1）计算系统开环与闭环的脉冲传递函数；2）计算当时使系统稳定的K值范围；3）计算当r（t）=1（t）时系统输出响应c∗（t）。

图11-5 闭环离散系统

解：1）计算系统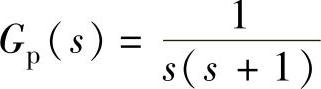与T=1s开环与闭环的脉冲传递函数。

clear；num=[1]；den=[110]；T=1；key=2；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到T=1s时、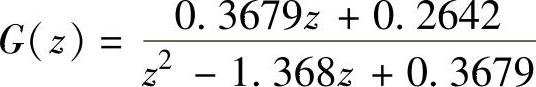

2）计算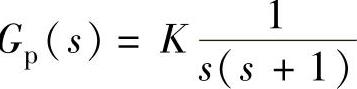系统闭环w域特征方程。

clear；syms w z K；Dzn=K∗（0.3679∗z+0.2642）；

Dzd=z^2-1.368∗z+0.3679；key=1；[Dw，Gw]=Dzw（key，Dzn，Dzd）；

程序运行后得到系统闭环w域特征方程为

D（w）=（0.6321∗K-0.0001）w²+（1.2642-0.5284K）w+（2.7359-0.1037K）=0

用Lienard-Chipard稳定判据计算系统稳定的K值范围。

要系统稳定，首先，特征方程的各项系数均应大于0，有系数a₀>0、a₁>0、a₂>0。其次，因系统最高阶n=2，则计算Hurwitz行列式中奇数阶子行列式D₁=a₁应大于0。

clear；syms a1 a2 a0 K；

a0=0.6321∗K-0.0001；

[K]=solve（0.6321∗K-0.0001=0）；K=vpa（K，4），

a1=1.2642-0.5284∗K；

[K]=solve（1.2642-0.5284∗K=0）；K=vpa（K，4），

a2=2.7359-0.1037∗K；

[K]=solve（2.7359-0.1037∗K=0）；K=vpa（K，4），

程序运行后得到0.0001582<（K）<2.393。

3）用MATLAB符号计算法计算r（t）=1（t）时的系统输出响应c∗（t）。

clear；syms z；Rz=z/（z-1）；H=8；phiz=（0.3679∗z+0.2642）/（z^2-z+0.6321）；[cn]=phiRz（phiz，Rz，H）；

程序运行后得到

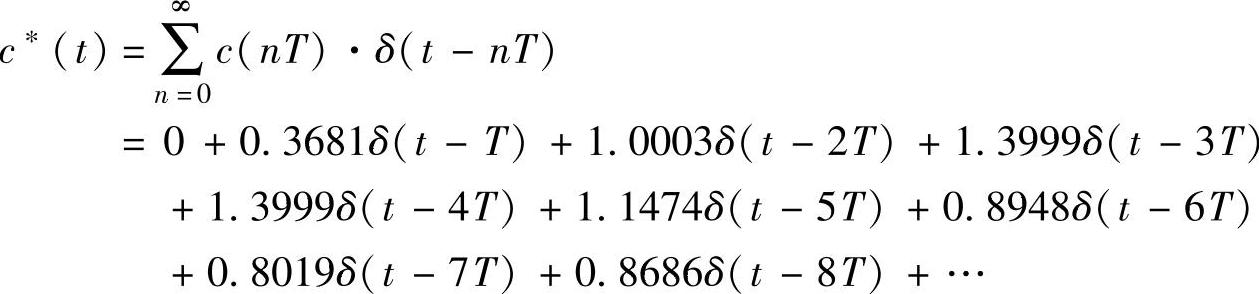
【例11-15】 续上题，1）绘制系统单位阶跃响应曲线；2）用单位阶跃响应验证开环增益K>2.4时系统是否稳定；3）绘制系统单位斜坡响应曲线；4）绘制系统单位冲激响应曲线。

解：1）绘制单位阶跃响应曲线。

clear；num=[0.36790.2642]；den=[1-10.6321]；n=50；dstep（num，den，n），grid；

程序运行后绘制出当K=1时的单位阶跃响应曲线，如图11-6所示。

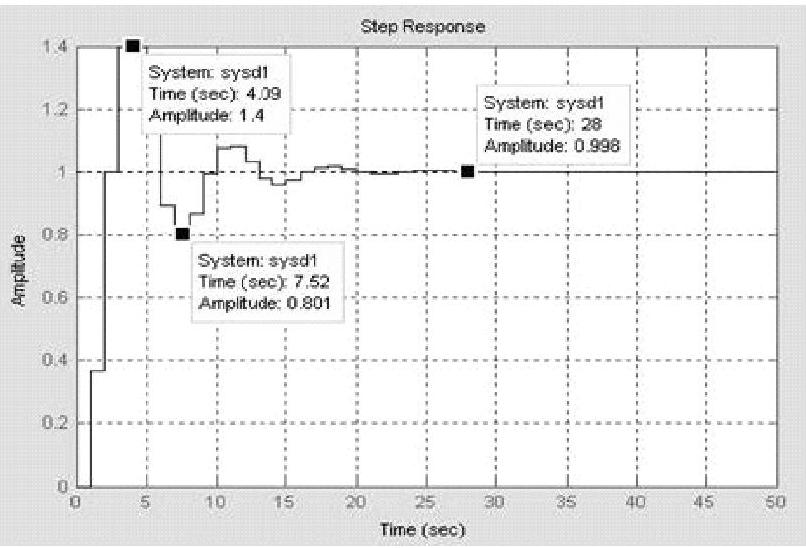
图11-6 当K=1时单位阶跃响应曲线(www.xing528.com)

2）验证临界开环增益K>2.393时，系统是否稳定。

①取K=2.5时计算Φ（z）。

clear；num=[2.5]；den=[110]；T=1；key=2；

[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到当K=2.5时Φ（z）=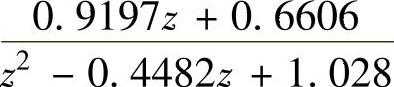

②当K=2.5时再次绘制单位阶跃响应曲线。

clear；num=[0.91970.6606]；den=[1-0.4482

1.028]；

n=280；dstep（num，den，n），grid；

程序运行后绘制出当K=2.5时的单位阶跃响应曲线，如图11-7所示。由曲线可知，单位阶跃响应是发散的振荡，说明当K>2.393时系统确实不稳定。

3）绘制系统单位斜坡响应曲线。

clear；n=[1]；d=[110]；G=tf（n，d）；

G1=feedback（G，1）；dt=0.6；Gz=c2d（G1，dt）；

[nz，dz]=tfdata（Gz，v）；

ts=0：dt：40；dlsim（nz，dz，ts）；grid；

程序运行后绘制出当K=1时系统单位斜坡响应曲线，如图11-8所示。

图11-7 当K=2.5时单位阶跃响应曲线

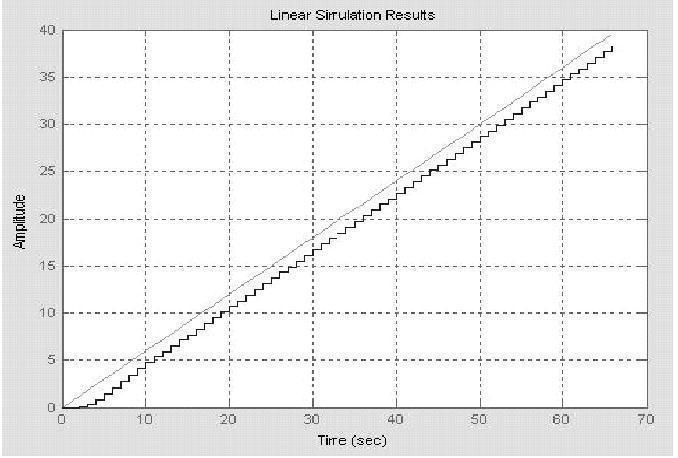
图11-8 当K=1时单位斜坡响应曲线

4）绘制系统单位冲激响应曲线。

clear；num=[0.36790.2642]；den=[1-10.6321]；

n=50；dimpulse（num，den，n），grid；

程序运行后绘制系统单位冲激响应曲线，如图11-9所示。还可以用以下程序绘制系统单位冲激响应离散杆图，如图11-10所示。

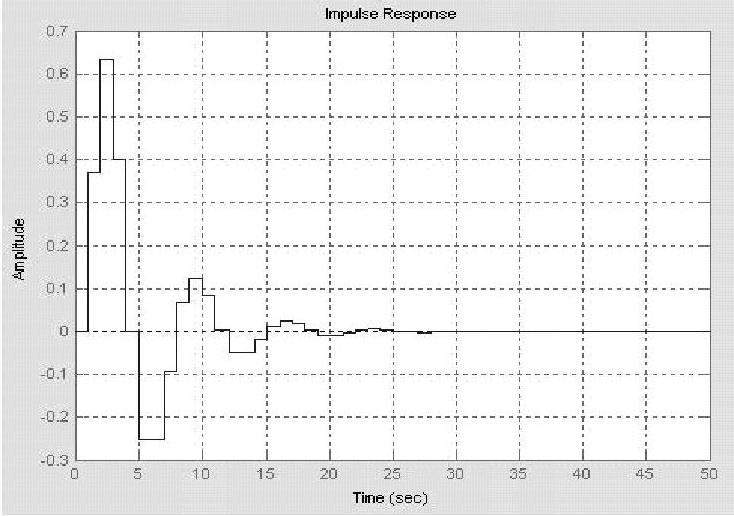
图11-9 系统单位冲激响应曲线

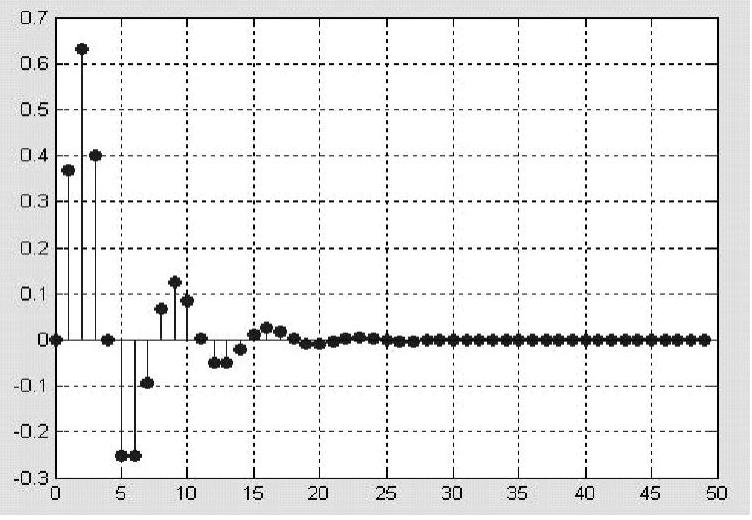
图11-10 单位冲激响应离散杆图

clear；num=[0.36790.2642]；den=[1-10.6321]；n=50；t=0：1：49；

[y，x]=dimpulse（num，den，n）；stem（t，y，filled），grid；