离散控制系统的脉冲传递函数介绍

离散控制系统的脉冲传递函数是分析线性离散系统的基础。设开环离散系统如图11-1所示，在零初始条件下，连续输入信号r（t）采样后r^∗（t）的z变换为R（z），系统连续部分的输出为c（t），采样后c^∗（t）的z变换为C（z），则线性定常离散系统的脉冲传递函数定义为系统输出采样信号的z变换C（z）与输入采样信号的z变换R（z）之比，记作

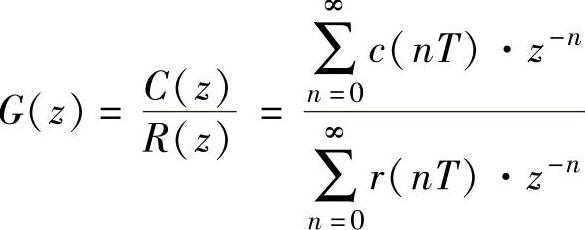
从上式可知，已知输出采样信号的z变换C（z）与输入采样信号的z变换R（z）以及脉冲传递函数G（z）三者中的两者就可以求出第三者。

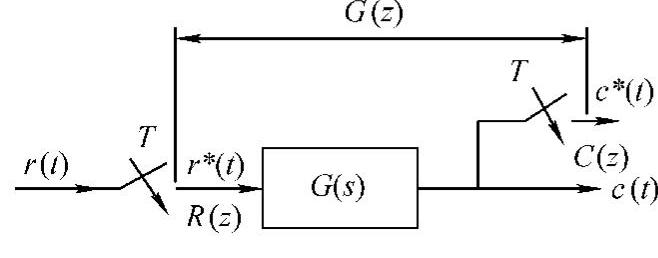
图11-1 开环离散系统

【例11-8】 已知离散系统脉冲传递函数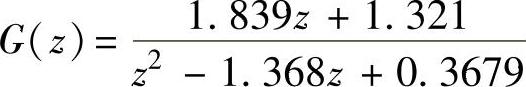、采样开关的采样周期T=1 s。若输入信号的z变换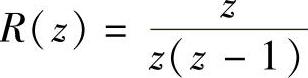，试求系统输出信号c（nT）T=1=c（n）与

c∗（t）。

解：

clear；syms z；Rz=z/（z-1）；H=8；Gz=（1.839∗z+1.321）/（z-1）/（z-0.3679）；

phiz=Gz；[cn]=phiRz（phiz，Rz，H）；

程序运行后得到

cn=-5.000+5.000∗.3679^n+4.999∗n

cn0=0

cn1=1.8385

cn2=5.6748

cn3=10.2460

cn4=15.0876

cn5=20.0287

cn6=25.0064

cn7=29.9976

cn8=34.9937

即系统输出采样信号c（n）=-5+4.999n+5×（0.3679）n与

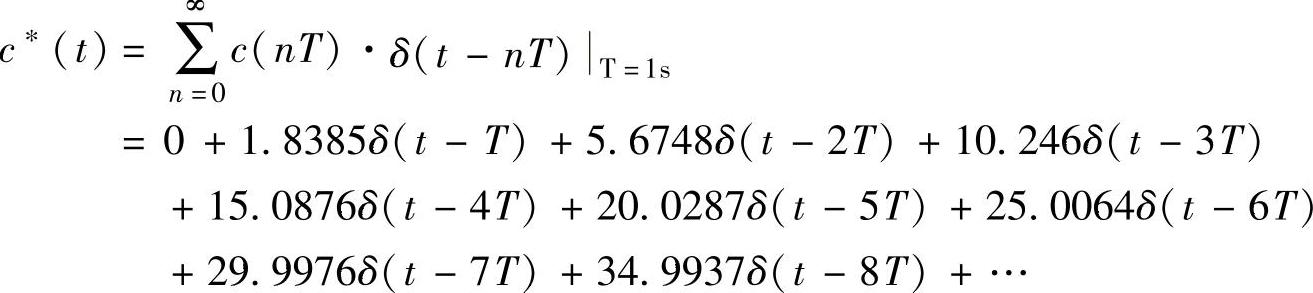
【例11-9】 开环离散系统如图11-1所示，其连续部分传递函数为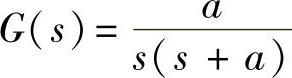，试求该开环离散系统的脉冲传递函数G（z）及当a=8时的G（z）。

解：根据自动控制原理，如果连续系统的传递函数为G（s），其系统脉冲过渡函数为g（t），那么有g（t）=L^-1[G（s）]与。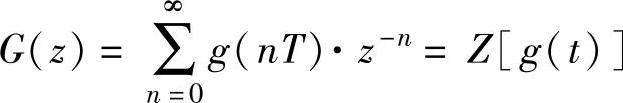

clear；syms s a；G1s=a/s；G2s=1/（s+a）；key=1；

[Gz]=seriz（key，G1s，G2s）；Gz=subs（Gz，a，8），

程序运行后得到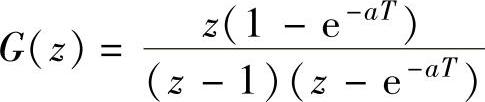

当a=8时。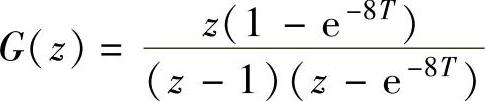

【例11-10】 开环系统结构如图11-2所示，图中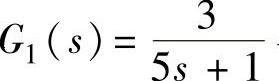与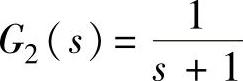，试求系统的脉冲传递函数G（z）及当采样开关采样周期T=1s时的G（z）。

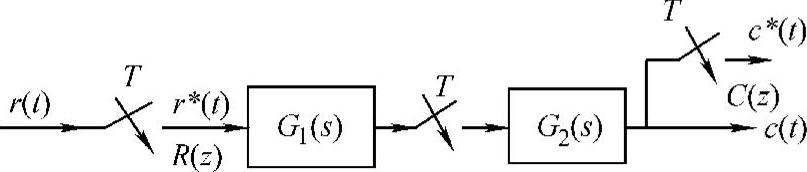
图11-2 有零阶保持器的开环系统

解：

clear；syms s T；G1s=3/（5∗s+1）；G2s=1/（s+1）；key=2；

[Gz]=seriz（key，G1s，G2s）；Gz=subs（Gz，T，1），

程序运行后得到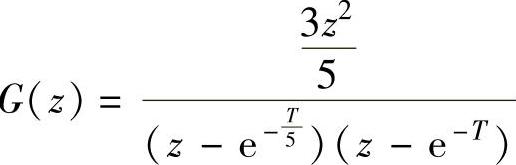

当T=1s时。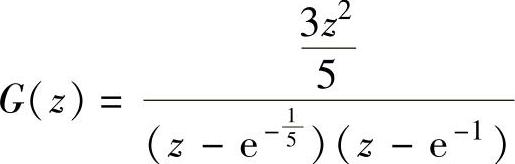

【例11-11】 具有零阶保持器的开环系统结构如图11-3所示，其零阶保持器与连续部分传

递函数分别为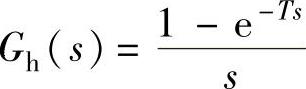与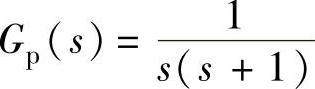，采样开关的采样周期T=1s，试求系统开环脉冲传递函数G（z）。(https://www.xing528.com)

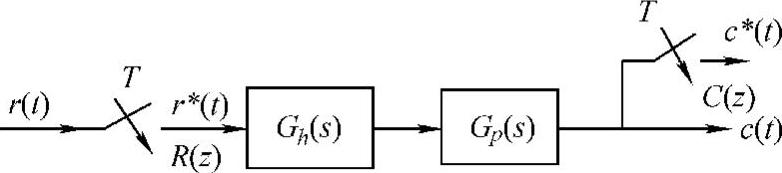
图11-3 有零阶保持器的开环系统

解：

clear；num=[1]；den=[110]；T=1；

key=1；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到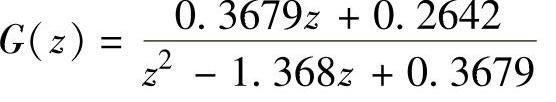

【例11-12】 闭环离散系统结构如图11-4所示，其前向通道零阶保持器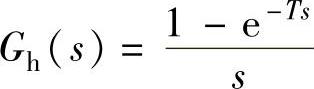，采样开关的采样周期与连续部分传递函数分别为1）T=1s、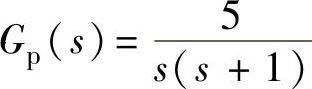、2）T=0.2s与T=0.05s、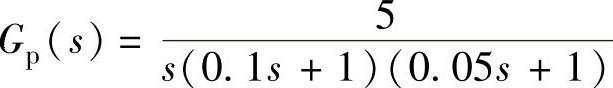、3）T=1s与T=0.1s、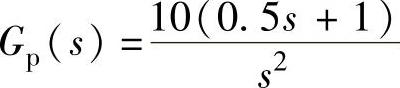、4）T=1s、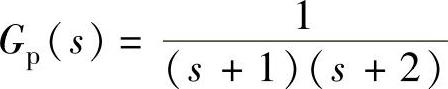，试求4个开环与闭环系统脉冲传递函数G（z）与Φ（z）。

图11-4 闭环离散系统

解：1）。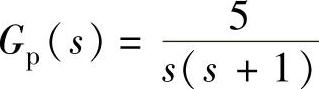

clear；num=[5]；den=[110]；T=1；

key=2；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到T=1s时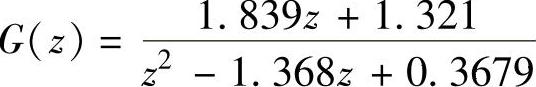

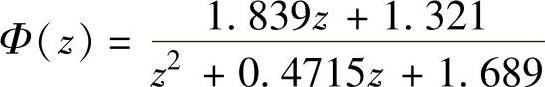
2）。

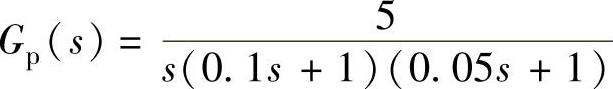clear；num=[5]；den=conv（[0.110]，[0.051]）；T=0.2；

key=2；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到T=0.2s时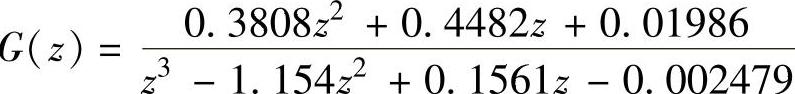

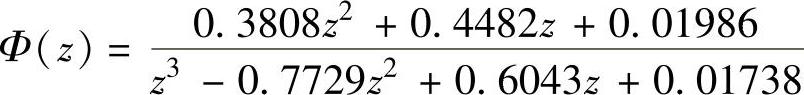
clear；num=[5]；den=conv（[0.110]，[0.051]）；T=0.05；

key=2；[Gz，phiz]=zohz（key，T，num，den）；

程序运行后得到T=0.05s时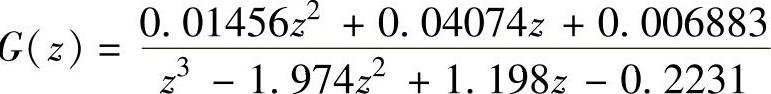

。

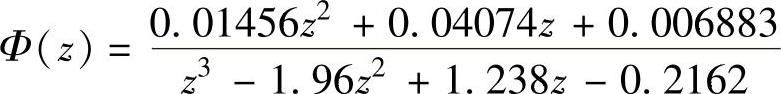
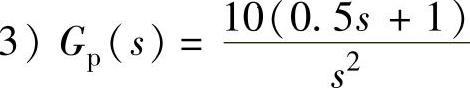读者可仿上例自行编写程序算得T=1s时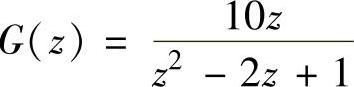、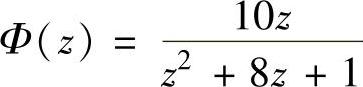，T=0.1s时、。

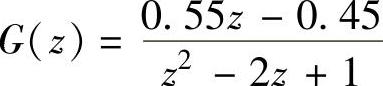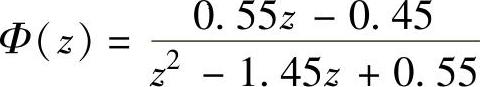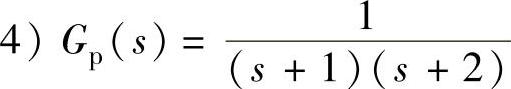
同样读者可仿上例自行编写程序算得T=1s时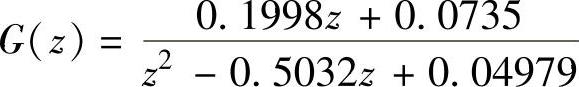

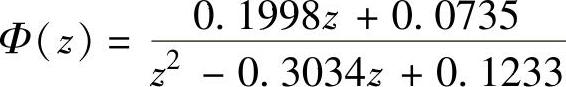
【例11-13】 已知离散系统状态空间方程

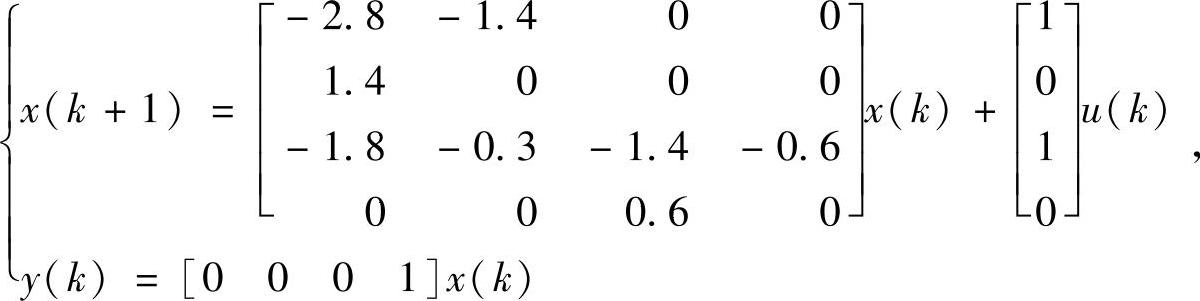
试求采样周期T=0.4s时系统传递函数模型的num、den、系统零极点增益模型与传递函数模型的DSP形式。

解：

clear；a=[-2.8-1.400；1.4000；-1.8-0.3-1.4-0.6；000.60]；

b=[1；0；1；0]；c=[0001]；d=[0]；

T=0.1；sys=ss（a，b，c，d，T）；sys1=tf（sys）；num=sys1.num{1}，

den=sys1.den{1}，sys2=zpk（sys），sys3=filt（num，den，T），

程序运行后可得传递函数模型的num、den、系统的零极点增益模型与传递函数模型的DSP形式分别为