用MATLAB工具解析Z变换和反变换

MATLAB系统为z变换与z反变换提供了专用函数以及多种调用格式。提请读者特别关注：①连续时间函数e（t）经过采样，只在离散的t=nT处取值即e（nT），于是e（t）的采样值就为e（nT）。②定义z反变换Z^-1[E（z）]=e（nT）或Z^-1[E（z）]=e^∗（t），两者一致。MATLAB系统提供的z反变换函数求出的是e（nT）。若待求解的是e^∗（t），只要将e（nT）带入采样函数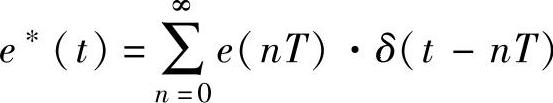即可。请看示例。

【例11-1】 对函数1）f（t）=1-e^-at、2）f（t）=sin（ωt）e^-at计算其z变换F（z）。

解：1）f（t）=1-e^-at。

clear；syms a n z t T；f=1-exp（-a∗n∗T）；F=simple（ztrans（f））；

[n，d]=numden（F）；F=n/d，

程序运行后得到。

2）f（t）=sin（ωt）e^-at。

clear；syms a n z T omega；

f=sin（omega∗n∗T）∗exp（-a∗n∗T）；F=simple（ztrans（f）），

程序运行结果

【例11-2】 试对函数1）f（n-2）、2）f（n-1）计算其z变换F（z）。

解：1）f（n-2）。

clear；syms n z；F=ztrans（sym（f（n-2））），

语句运行结果。

2）f（n-1）。

clear；syms n z；F=ztrans（sym（f（n-1））），

语句运行结果。

【例11-3】 对函数1）f（t）=te^-at、2）f（t）=t·e（t）求其F（z）。

解：1）f（t）=te^-at。

clear；syms a n z T；f=n∗T∗exp（-a∗n∗T）；F=ztrans（f），

语句运行后得到

作为特例，当T=1时

2）f（t）=t·e（t）。

clear；syms n z T；f=n∗T∗sym（e（n∗T））；

F=ztrans（f），F=subs（F，T，1），

语句运行结果，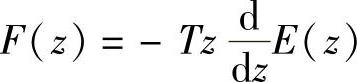

当T=1时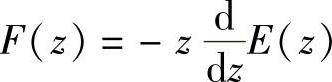，此题结论就是z域微分定理。

【例11-4】 对z变换式，试求z反变换f（n）；当a=10、b=1与c=2时，再对求z反变换f∗（t）。(https://www.xing528.com)

解：1）求其z反变换f（n）。

clear；syms a b c n z；F=a∗z/（（z-b）∗（z-c））；f=iztrans（F），

语句运行结果。

2）当a=10、b=1与c=2时求的反变换f^∗（t）。

clear；syms n z；F=10∗z/（（z-1）∗（z-2））；f=iztrans（F），

语句执行后得到z反变换为f（n）=Z^-1[F（z）]=10（2ⁿ-1），即

【例11-5】 对z变换1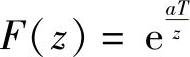）、2），试求其z反变换f（nT）。

解：1）。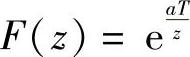

clear；syms a z n T；f=iztrans（exp（a∗T/z）），

语句执行后得到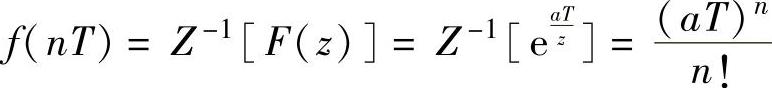

当T=1时，显然有

当T=1与a=1时，则有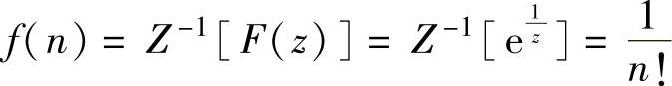

2）。

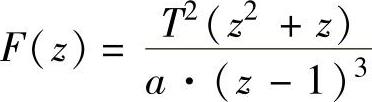clear；syms z t T a；F=T^2∗（z^2+z）/（a∗（z-1）^3）；f=iztrans（F），

语句执行结果

即。当a=2时，求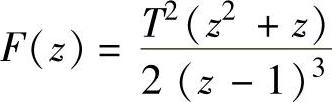的z反变换即。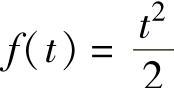

【例11-6】 试确定1）、2）、3）E（z）=函数的初值与终值。

解：1）。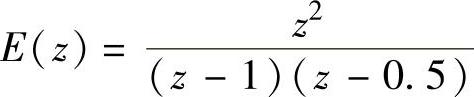

clear；syms z；Ez=z^2/（z-0.5）/（z-1）；[essini，essend]=iniendz（Ez）；

程序运行后得到函数初值e（0）=1与终值e_ss（∞）=2。

2）。

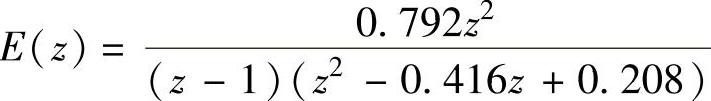clear；syms z T；Ez=0.792∗z∗z/（z-1）/（z^2-0.416∗z+0.208）；[essini，essend]=iniendz（Ez）；

程序运行后得到函数初值e（0）=0与终值e_ss（∞）=1。

3）。

clear；syms z；Ez=z∗（z+0.5）/（z-1）/（z^2-0.5∗z+0.3125）；[essini，essend]=iniendz（Ez）；

程序运行后得到函数初值e（0）=0与终值e_ss（∞）=1.8462。