MATLAB实现描述函数法分析非线性系统自振

在以下描述函数法分析非线性系统自振的MATLAB实现中，必须绘制系统线性部分在频率范围0≤ω≤+∞的幅相特性，即Nyquist曲线。《控制系统MATLAB计算及仿真》中已经说明过，MATLAB中的函数命令nyquist（）执行后绘制的是在-∞≤ω≤+∞范围的完整开环频率响应G（jω）H（jω），范围-∞≤ω≤0与0≤ω≤+∞的两个部分Nyquist曲线对称于复平面的横轴。提请读者要特别关注从横轴下方穿到横轴上方趋向原点这一分支曲线即0≤ω≤+∞区段内的曲线情况。

【例10-1】 设带有死区特性的系统结构如图10-4所示，其中参数Δ=0.1，K=1。线性部分的传递函数为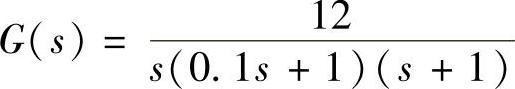。试分析该系统是否存在自振。若有自振，需求出自振振幅X与角频率ω。

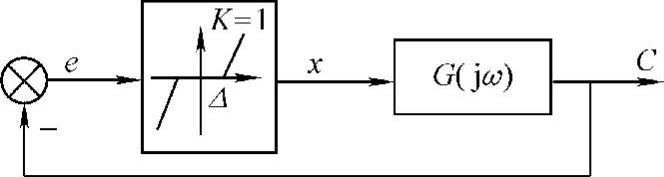
图10-4 带有死区特性的系统

解：1）系统线性部分传递函数为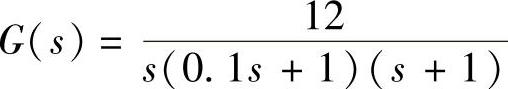，那么，线性部分频率特性为

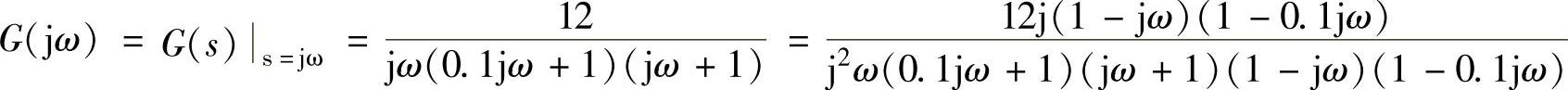
2）负倒描述函数与负倒描述函数图。

①死区特性的描述函数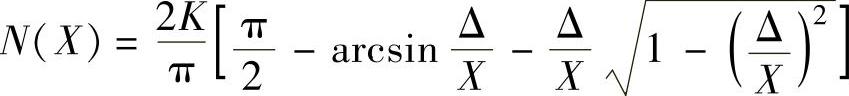，已知Δ=0.1，K=1，故有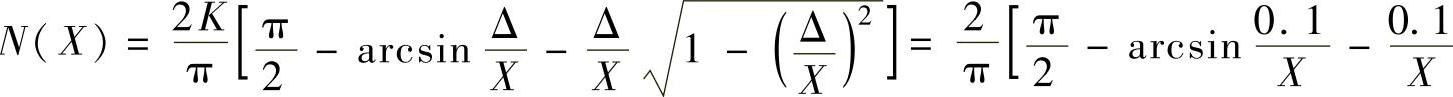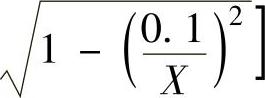。负倒描述函数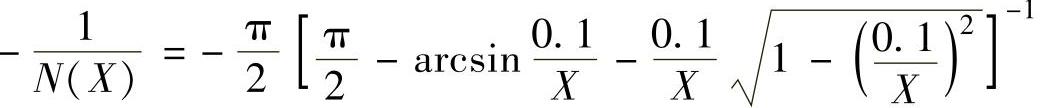，所有N（X）与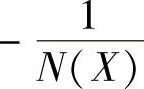都是X的实数函数。

②负倒描述函数图。当X=Δ=0.1时，N（X）=0、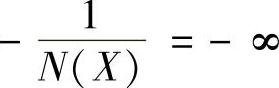；当X=∞时，N（X）=K、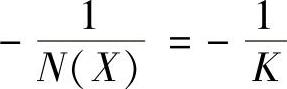。据此得到带有死区特性的负倒描述函数图，如图10-5所示。请特别注意X增大的方向，这在判断自振点性质时尤其重要。

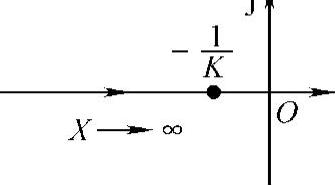
图10-5 带有死区特性的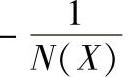

3）因为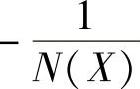是X的实数函数，与G（jω）画在同一复平面内时，交点必在横坐标上，G（jω）虚部为零，求交点的角频率ω与交点的|G（jω）|。

①分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）部分：

clear；syms w Gn；Gn=12∗j∗（1-j∗w）∗（1-0.1∗j∗w）；Gn=expand（Gn），

程序运行结果Gn=12∗i+66/5∗w-6/5∗i∗w^2。

②利用交点的虚部为零，求交点的角频率ω。

clear；syms w；[w]=solve（12-6/5∗w^2=0，w）；w=vpa（w，4），

程序运行后得到交点的角频率。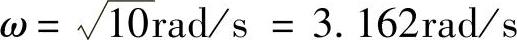

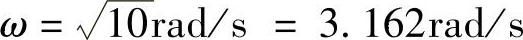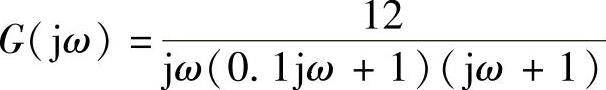③由交点，按计算交点。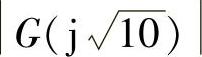

clear；syms w U；w=sqrt（10）；G=12/（j∗w∗（0.1∗j∗w+1）∗（j∗w+1））；U=real（G），

程序运行后得到。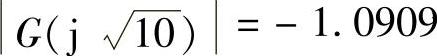

④利用交点在横坐标上，即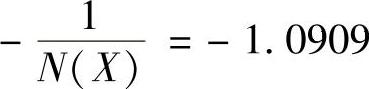，求自振的振幅X。

clear；syms X；

[X]=solve（pi/2/（pi/2-asin（0.1/X）-0.1/X∗sqrt（1-（0.1/X）^2））=1.0909，X）；X=vpa（X，4），

程序运行后得到X=1.527。

4）执行以下MATLAB程序使在同一复平面上绘制非线性特性负倒描述函数与线性部分的Nyquist曲线，以便观察其交点。

clear；

for X=0.1：0.1：20

x=2/pi∗（pi/2-asin（0.1/X）-0.1/X∗sqrt（1-（0.1/X）^2））；

y=0；plot（-1/x，y，k∗），grid on；hold on；

end

n=[12]；d=conv（conv（[10]，[11]），[0.11]）；G=tf（n，d）；

for w=1.8：0.1：80

nyquist（G，[w，w+0.1]），grid on；hold on；

end

程序运行后绘制带有死区特性负倒描述函数与线性部分Nyquist曲线，如图10-6所示，其示意图如图10-7所示。

由图10-7可以看出，系统的G（jω）与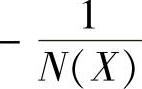有一个交点且在横轴上。交点的角频率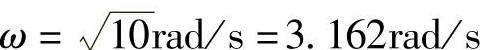，交点的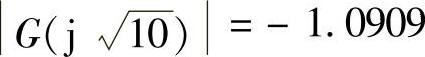。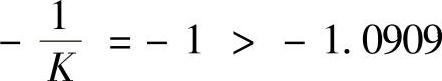，按图10-3中M₁交点的分析，不是自振点，计算的自振角频率与自振振幅都无意义。

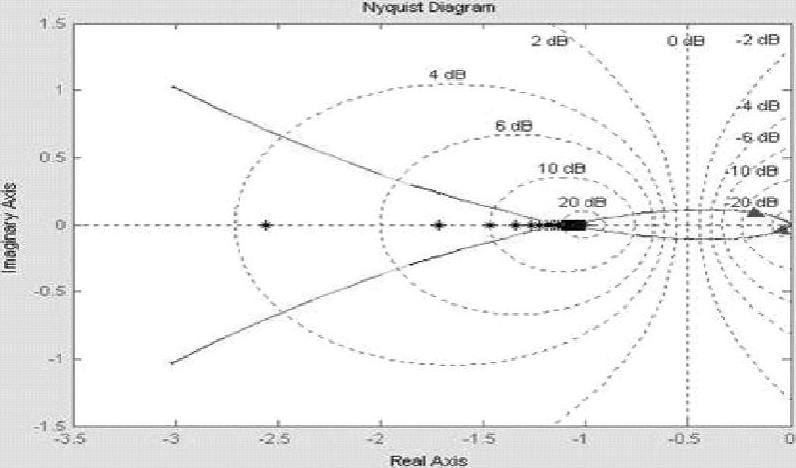
图10-6 系统的G（jω）与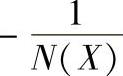曲线

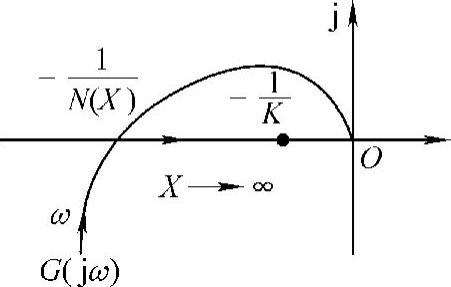
图10-7　G（jω）与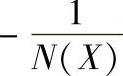交点示意图

在此特别提请读者关注以下三点。

①程序运行的时间可长达数分钟之久，是因为计算工作量太大，不要误认为是死机。

②为了方便地绘制出曲线，可根据程序中两个循环语句循环变量的起始值与终了值的范围，分成数段进行，以收到立竿见影的效果。显然，分成的数段应彼此衔接，以便使曲线连续。还要注意，步长越小，绘制的曲线越精细美观，而运算的时间越长。

③由于带有死区特性的描述函数是自振振幅X的实函数，其相对负倒描述函数也是自振振幅X的实函数，其虚部为零，曲线在负实轴上，与系统线性部分Nyquist曲线的交点也在横坐标上。

以上三点说明，对本章其他的题目也都适用。非线性特性描述函数是X复函数者除外。

【例10-2】 设带有理想继电特性的系统结构如图10-8所示，其中参数为M=1，线性部分的传递函数为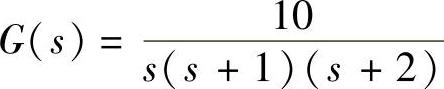。试分析系统是否存在自振，若有自振，试求振幅X与角频率ω。

解：1）系统线性部分的传递函数为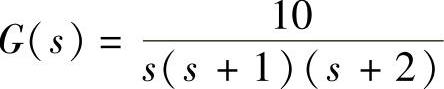，则其频率特性为

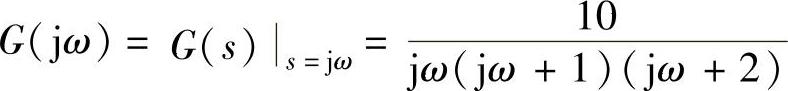
2）书写负倒描述函数与绘制负倒描述函数图。

①理想继电特性的描述函数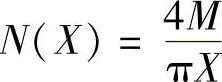，负倒描述函数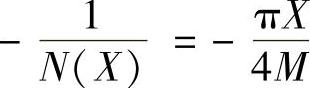，N（X）与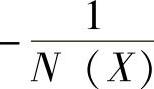都是X的实数函数。

②负倒描述函数图。当X=0时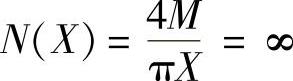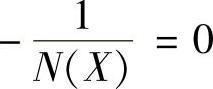，、；当X=∞时，N（X）=0、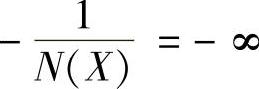。据此得到理想继电特性的负倒描述函数图如图10-9所示。已经说明过，请特别注意X增大的方向，这在判断自振点性质时尤其重要。

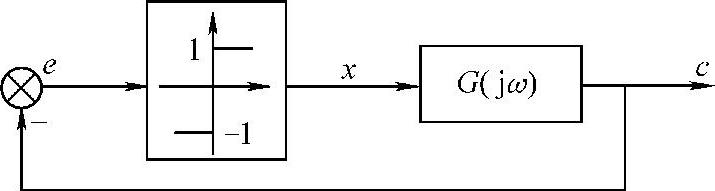
图10-8 带有理想继电特性的系统

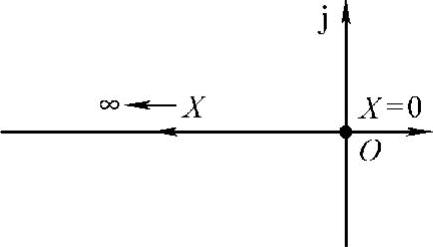
图10-9 理想继电特性的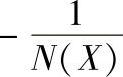

3）对于线性部分的频率特性，利用交点在横坐标上，其虚部为零，求交点的角频率ω与交点的G（jω）。

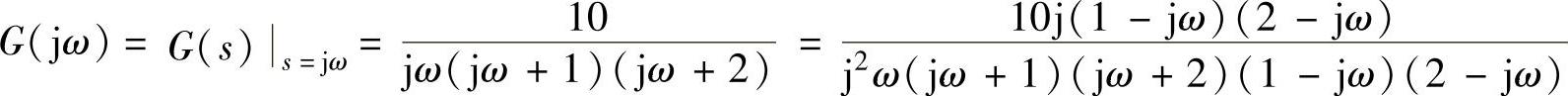
①分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）：

clear；syms w n；n=expand（j∗（1-1∗j∗w）∗（2-1∗j∗w）），

程序段运行结果n=2∗i+3∗w-i∗w^2。

②利用交点的虚部为零，求交点的角频率ω。

clear；[w]=solve（2-w^2=0）；w=vpa（w，4），

序段运行后得到交点的角频率ω=1.4142rad/s。

③由交点的角频率ω=1.4142rad/s，按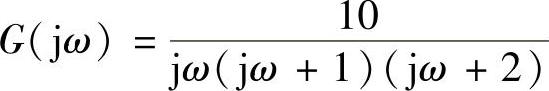计算交点的|G（j1.414）|。

clear；w=1.414；G=10/（j∗w∗（j∗w+1）∗（j∗w+2））；A=real（G），

程序段运行后得到|G（j1.414）|=-1.6672。

④利用交点在横坐标上，即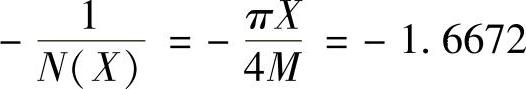，求自振的振幅X。

clear；syms X；[X]=solve（pi∗X/4=1.6672，X）；X=vpa（X，4），

程序段运行结果X=2.123。

4）执行以下MATLAB程序使在同一复平面上绘制非线性特性负倒描述函数与线性部分的Nyquist曲线，以便观察其交点。

clear；M=1；

for X=0.01：0.1：10

x=4/pi/X；y=0；plot（-1/x，y，k∗），

grid on；hold on；

end

n=[0 0 0 1 0]；d=conv（conv（[1 0]，[1 1]），[1 2]）；G=tf（n，d）；

for w=0.8：0.1：6

nyquist（G，[w，w+0.1]），

grid on；hold on；

end

程序运行后绘制带有理想继电特性的负倒描述函数与线性部分Nyquist曲线，如图10-10所示，其示意图如图10-11所示。

5）结论。线性部分的频率特性曲线与相对负描述函数有一个交点，交点的角频率ω=1.414rad/s，G（j1.414）=-1.6672，自振的振幅X=2.123，对应着系统一次近似下的周期运动状态。类似图10-3中M₂交点的分析，确定该点是自振点。

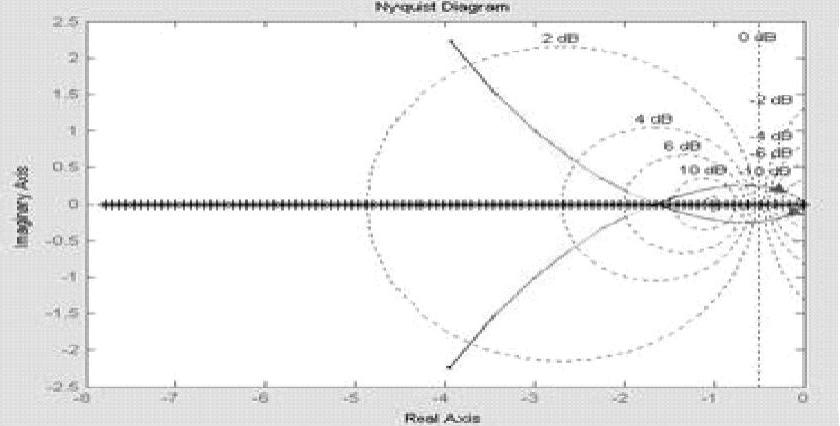
图10-10 系统的G（jω）与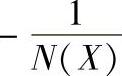曲线

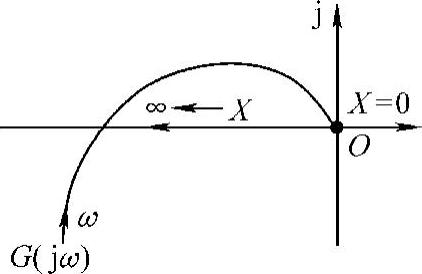
图10-11 图10-10示意图

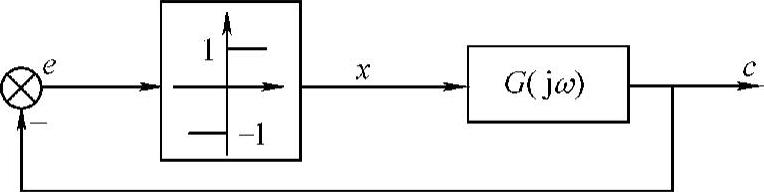
图10-12 带有理想继电特性的系统

【例10-3】 设带有理想继电特性的系统结构如图10-12所示，其中参数为M=1，线性部分的传递函数为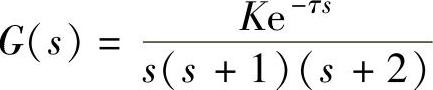。1）当τ=0时，要产生振幅为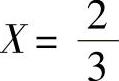的自振，K应取何值？自振角频率ω为何值？2）当τ>0时，要产生振幅为X=2与角频率ω=1rad/s的自振，τ与K应取何值？

解：1）当τ=0、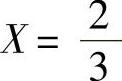时，求K与ω。

①系统的线性部分的传递函数为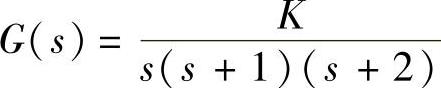，那么，线性部分的频率特性为。

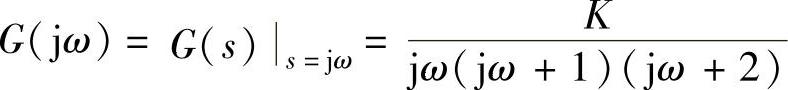②对于线性部分的频率特性，利用交点在横坐标上，其虚部为零，求交点的角频率ω与交点的|G（jω）|。

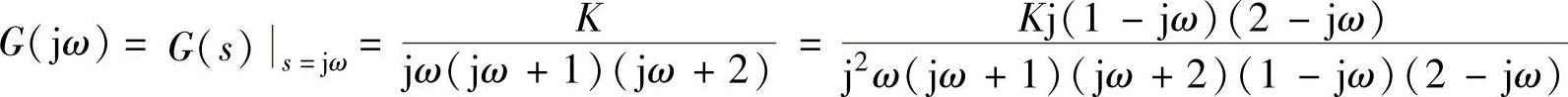
分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）：

clear；syms w n；n=expand（j∗（1-1∗j∗w）∗（2-1∗j∗w）），

程序段运行结果n=2∗i+3∗w-i∗w^2。

利用交点的虚部为零，求交点的角频率ω。

clear；[w]=solve（2-w^2=0）；w=vpa（w，4），

程序段运行后得到交点角频率ω=1.414rad/s。

由交点的角频率ω=1.414rad/s，按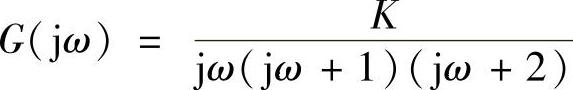计算交点的|G（j1.414）|：

clear；syms G A w；syms K real；w=1.414；

G=K/（j∗w∗（j∗w+1）∗（j∗w+2））；A=abs（G）；A=vpa（A，4），

程序段运行后得到|G（j1.414）|=0.1668K。

③对于负倒描述函数，利用交点在横坐标上，其虚部为零，求K。

理想继电特性的描述函数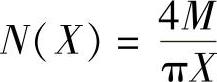，负倒描述函数。

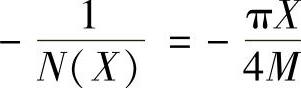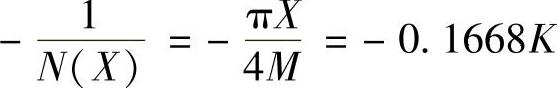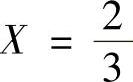利用交点在横坐标上，即，M=1，，求K。

clear；syms K；[K]=solve（pi∗（2/3）/4=0.1668∗K，K）；K=vpa（K，4），

程序段运行后得到K=3.139。

④结论。绘制的τ=0时的G（jω）曲线与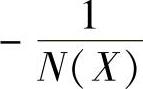曲线如图10-13所示。要产生振幅为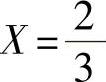的自振，应取K=3.139，此时自振的角频率ω=1.414rad/s。

2）当τ>0时，X=2与ω=1rad/s的自振，求τ与K。

①频率特性G（jω）与负倒描述函数曲线分析。

当τ>0时，线性部分相频特性为

φ（ω_g）=-90°-arctan（ω_g）-arctan（ω_g/2）-τω×57.3°

其G（jω）曲线是螺旋线，G（jω）与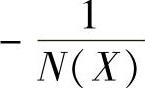有无穷多个交点，交点的相位为

-180°-k360°（k=0，1，2，…）

利用图10-3分析法，只有最左端的交点是自振点，绘制的τ>0时G（jω）曲线与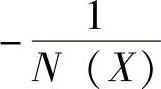曲线如图10-14所示。

②产生ω_g=1rad/s的自振时求τ。根据以上分析，有以下关系式

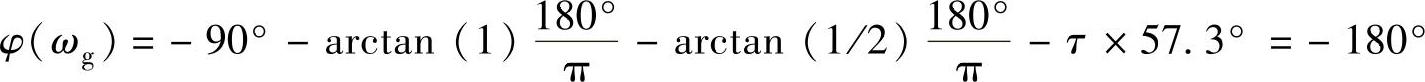
clear；syms tau；

[tau]=solve（90-atan（1）∗180/pi-atan（1/2）∗180/pi-tau∗57.3=0，tau）；

tau=vpa（tau，4），

程序运行后得到τ=0.3217。

③G（jω）与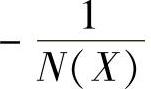相交时，。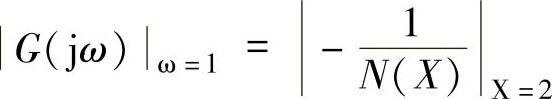

求|G（jω）|_ω=1。

clear；syms G A w；syms K real；w=1；

G=K/（j∗w∗（j∗w+1）∗（j∗w+2））；A=abs（G）；A=vpa（A，4），

程序运行结果A=0.3162∗abs（K）。

由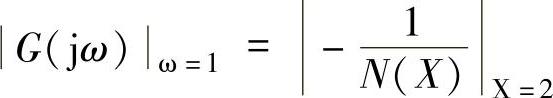求K。

理想继电特性的负倒描述函数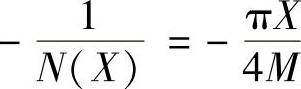，X=2，M=1。

clear；syms K；[K]=solve（pi∗2/4=0.3162∗K，K）；K=vpa（K，4），

程序运行结果后得到K=4.968。

④结论。当τ>0，要产生X=2与ω=1rad/s的自振，应取τ=0.3217与K=4.968。

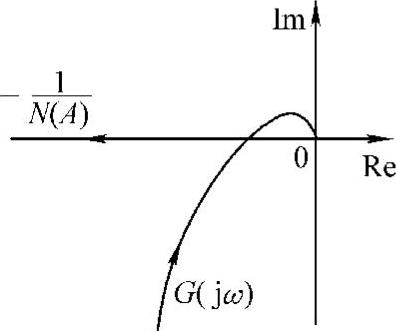
图10-13　τ=0时G（jω）与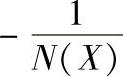

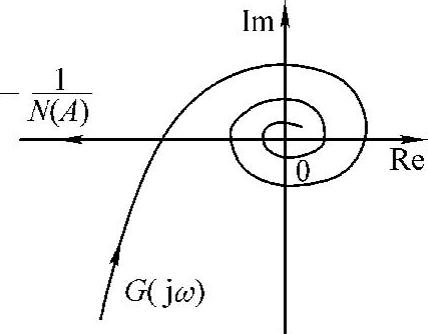
图10-14　τ>0时G（jω）与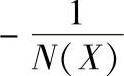

【例10-4】 设带有饱和特性的系统结构如图10-15所示，其中参数为a=1、K=2，线性部分的传递函数为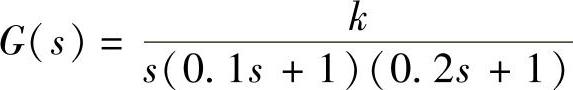。1）当k=15时，试分析该系统是否存在自振。若有自振，需求出自振的振幅X与角频率ω。2）试确定系统稳定时线性部分增益K的临界值K_c。

解：1）当k=15时，分析自振。

①系统的线性部分的传递函数为G（s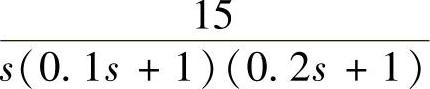）=，那么线性部分的频率特性为。

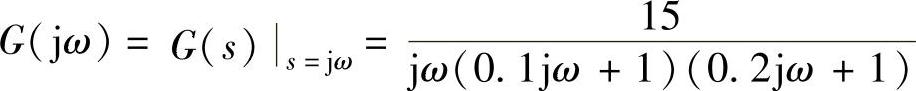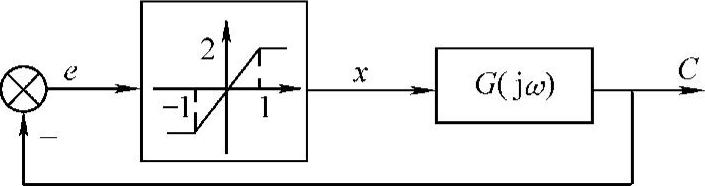
图10-15 带有饱和特性的系统

②负倒描述函数与负倒描述函数图。

饱和特性描述函数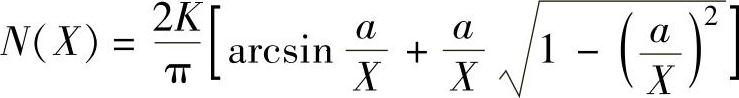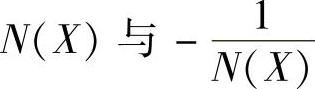，都是X实函数。当X=a时，N（X）=K、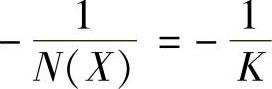；当X=∞时，N（X）=0、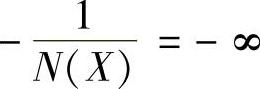。据此得到带有饱和特性的负倒描述函数图如图10-16所示。请特别注意X增大的方向。

③因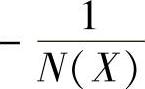是X实函数，与G（jω）画在同一复平面内时，交点必在横坐标上，其虚部为零，求交点角频率ω与交点的|G（jω）|。

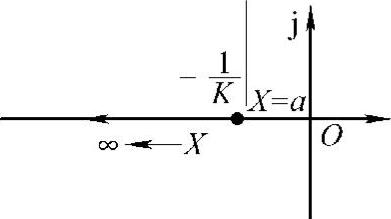
图10-16 带有饱和特性的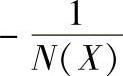

因为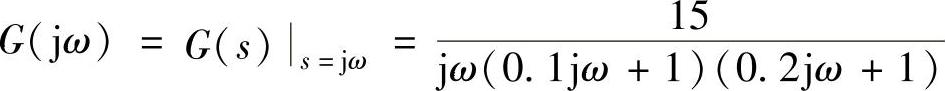

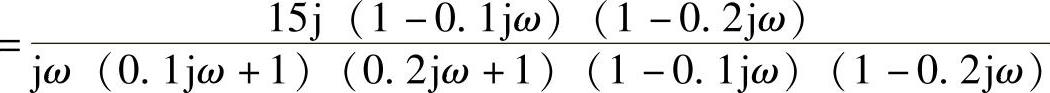
分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）：

clear；syms w n；

n=expand（j∗（1-0.1∗j∗w）∗（1-0.2∗j∗w）），

程序段运行结果n=i+3/10∗w-1/50∗i∗w^2。

利用交点的虚部为零，求交点的角频率ω。

clear；[w]=solve（1-1/50∗w^2=0）；w=vpa（w，4），

程序段运行后得到交点的角频率ω=0.707rad/s。

由交点的角频率ω=0.707rad/s，按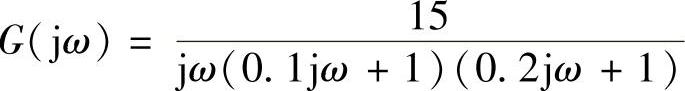计算交点的|G（j7.07）|。

clear；w=7.07；G=15/（j∗w∗（0.1∗j∗w+1）∗（0.2∗j∗w+1））；A=real（G），

程序段运行后得到|G（j7.07）|=-1.0003。

④利用负倒描述函数求自振的振幅X。

饱和特性描述函数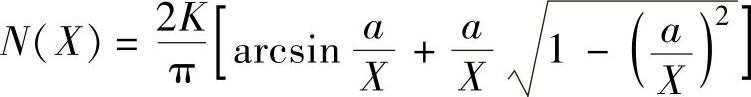，求负倒描述函数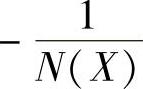表达式。

clear；syms X a K f；

a=1；N=2∗K/pi∗（asin（a/X）+a/X∗sqrt（1-（a/X）^2））；

f=-1/N；f=subs（f，K，2），

程序段运行结果f=-1/4∗pi/（asin（1/X）+1/X∗（1-1/X^2）^（1/2））。

利用交点在横坐标上，即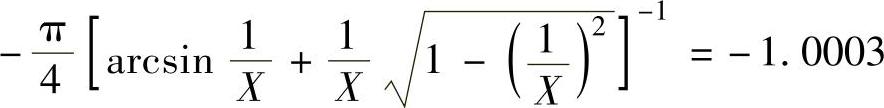，求自振振幅X。

变换以上表达式，得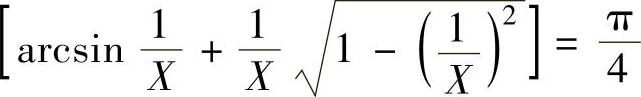

clear；syms X；

[X]=solve（asin（1/X）+1/X∗（1-1/X^2）^（1/2）=pi/4，X）；X=vpa（X，4），

程序段运行后得到X=2.475。

⑤在同一复平面用程序绘制G（jω）与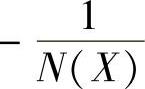曲线，以观察其交点情况。

clear；syms S k x y X；

S=1；k=2；

for X=0.5：0.01：4

x=2∗k/pi∗（asin（S/X）+S/X∗sqrt（1-（S/X）^2））；

y=0；plot（-1/x，y，k∗），hold on；

end

n=[00015]；

d=conv（conv（[10]，[0.11]），[0.21]）；G=tf（n，d）；

for w=5：0.1：30

nyquist（G，[w，w+0.1]），grid on；hold on；

end

程序运行后绘制G（jω）与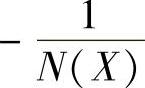曲线，如图10-17所示，其示意图如图10-18所示。(https://www.xing528.com)

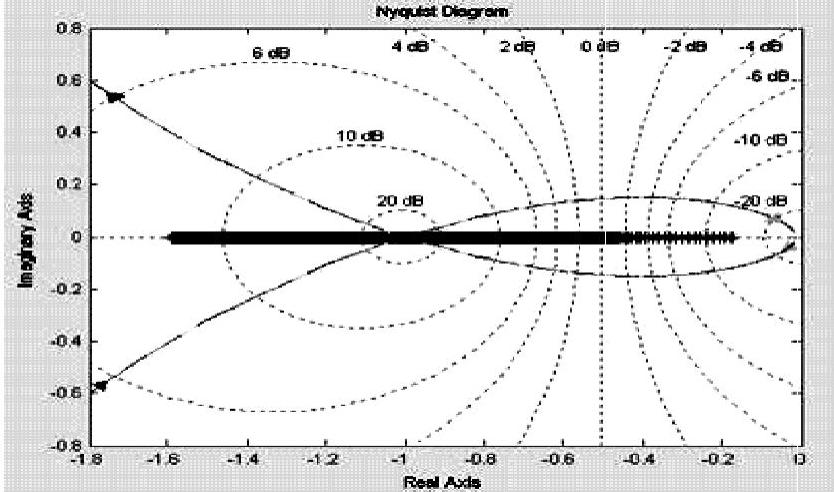
图10-17　G（jω）与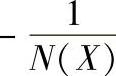曲线

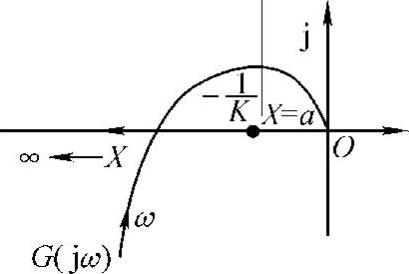
图10-18　G（jω）与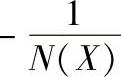曲线示意图

由图10-18可知，线性部分的频率特性曲线与相对负描述函数有一个交点，交点的角频率ω=0.707rad/s，自振的振幅X=2.475。对应着系统一次近似下的周期运动状态，按图10-3中M₂点的分析，确定该点是自振点。

2）确定系统稳定时线性部分增益k的临界值K_c。

①根据自动控制原理，对饱和非线性特性，当X=S时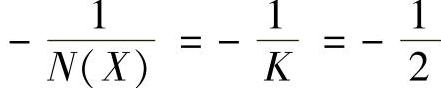，；而当X=∞时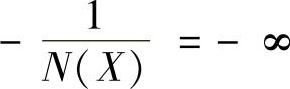，。欲使系统稳定，则线性部分频率特性G（jω）曲线需不包围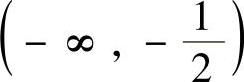线段。

②线性部分的频率特性曲线与相对负描述函数的交点，其角频率ω=7.07rad/s，求G（j7.07）的表达式（含有线性部分增益K变量）。

clear；syms w G U；syms Kc real；

w=7.07；G=Kc/（j∗w∗（0.1∗j∗w+1）∗（0.2∗j∗w+1））；

U=abs（G）；U=vpa（U，4），

程序运行结果U=.6668e-1∗abs（Kc）。

③确定增益k的临界值K_c。

clear；syms Kc；

[Kc]=solve（.6668e-1∗abs（Kc）=1/2，Kc）；Kc=vpa（Kc，4），

程序运行后得到增益k的临界值K_c=7.499。

【例10-5】设带有死区继电特性的系统如图10-19所示，并且死区特性的参数M=3、h=1，线性部分的传递函数为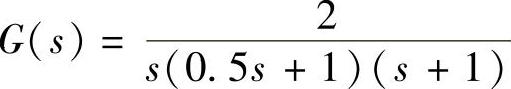，试分析该系统是否存在自振。若有自振，需求出自振的振幅X与角频率ω。

解：1）线性部分的频率特性为。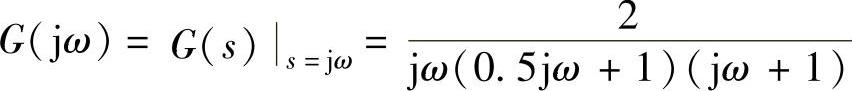

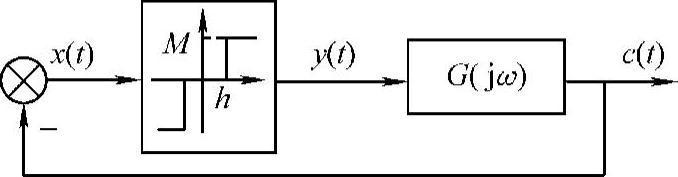
图10-19 带有死区继电特性的系统

2）求死区继电特性的负倒描述函数的极值条件。

①负倒描述函数的导函数。将负倒描述函数的导函数分解成分子与分母两部分。

clear；syms X M h；N=4∗M/pi/X∗sqrt（1-（h/X）^2）；

FN=-1/N；dFN=diff（FN，X）；[n，d]=numden（dFN），

程序运行后得到

n=-pi∗（X^2∗（1-h^2/X^2）-h^2）

d=4∗X^2∗M∗（1-h^2/X^2）^（3/2）

②令导函数分子部分为0对其计算负倒描述函数的极值条件。

clear；syms f N X M h；[X]=solve（-pi∗（X^2∗（1-h^2/X^2）-h^2）=0，X），

程序运行后得到极值条件为。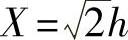

③计算负倒描述函数的极值。

clear；syms f N X M h；X=2^（1/2）∗h；f=-pi∗X/（4∗M∗sqrt（1-（h/X）^2）），

程序运行后得到。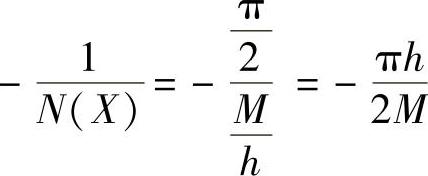

3）死区继电特性的描述函数与负倒描述函数图。

死区继电特性的描述函数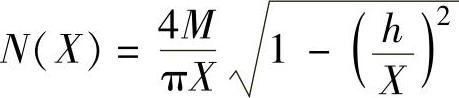，所以N（X）与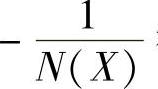都是X的实函数。当X=h时，N（X）=0、-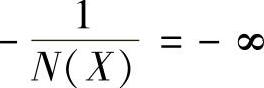；当X=∞时，N（X）=0、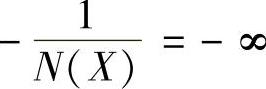。当时，函数出现极值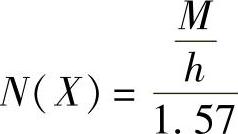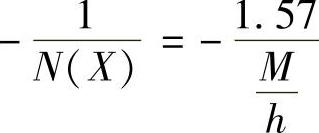，、。据此绘制带有死区继电特性的负倒描述函数图，如图10-20所示。请特别注意负倒描述函数图都在横坐标上，为分析方便画成分开的两支，并请注意X增大的方向、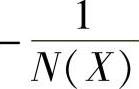图极值及其条件。

4）因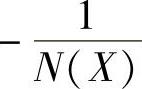是X实函数，与G（jω）画在同一复平面内时，交点必在横坐标上。利用虚部为零，求交点角频率ω与交点的|G（jω）|。

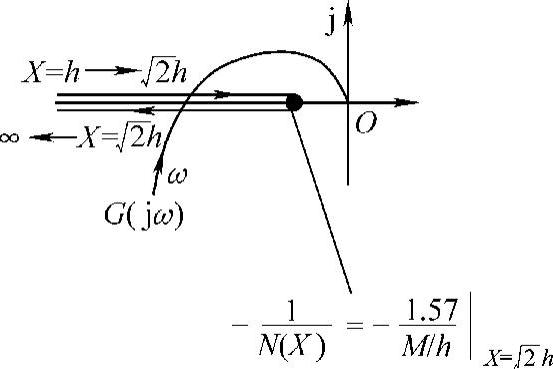
图10-20 带有死区继电特性的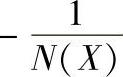

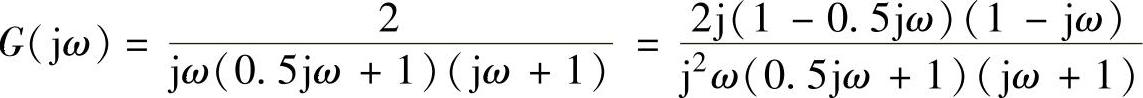
①分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）：

clear；syms w n；n=simple（j∗（1-1∗j∗w）∗（1-0.5∗j∗w）），

程序段运行结果n=i+3/2∗w-1/2∗i∗w^2。

②利用交点的虚部为零，求交点角频率ω。

clear；[w]=solve（1-1/2∗w^2=0），

程序段运行后得到交点角频率。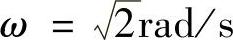

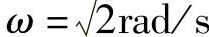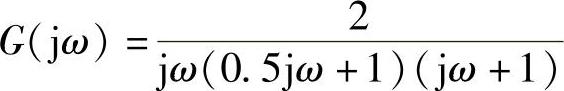③由交点，根据计算交点的。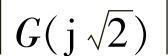

clear；w=2^（1/2）；G=2/（j∗w∗（0.5∗j∗w+1）∗（j∗w+1））；A=abs（G），

程序运行后得到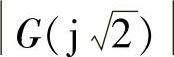=0.6667。

④对于负倒描述函数，利用交点在横坐标上，其虚部为零，求自振的振幅X。clear；syms X；[X]=solve（pi∗X/4/3/sqrt（1-（1/X）^2）=0.6667）；X=vpa（X，4），

程序运行后得到自振的振幅X₁=1.111与X₂=2.291。

5）在同一复平面用程序绘制G（jω）与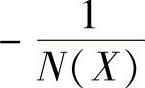曲线，以观察其交点情况。

clear；syms t x y z h M X；

M=3；h=1；

for X=0.7：0.1：10

x=4∗M/（pi∗X）∗sqrt（1-（h/X）^2）；y=0；plot（-1/x，y，k∗），hold on；

end

n=[0002]；d=conv（conv（[10]，[0.51]），[11]）；G=3/1∗tf（n，d）；

for w=1：0.1：8

nyquist（G，[w，w+0.1]），grid on；hold on；

end

程序运行后绘制的G（jω）与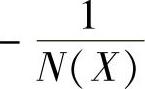曲线如图10-21所示，其示意图如图10-22所示。

6）结论。由图10-22可知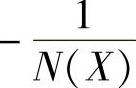，与G（jω）有两个交点，交点的角频率为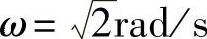，自振有两个振幅X₁=1.111与X₂=2.291，对应着系统两个一次近似下的周期运动状态，究竟哪个交点是自振点呢？类似图10-3中M₂交点的分析，确定X₂=2.291是自振点。

【例10-6】 已知带有死区继电特性的系统结构如图10-19所示，线性部分的传递函数为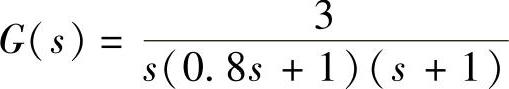，为使系统不产生自振，试利用描述函数法确定死区继电特性参数M与h之间的关系。

解：1）死区继电特性的描述函数与负倒描述函数都是X的实数函数，其矢端轨迹都在复平面的横轴上。其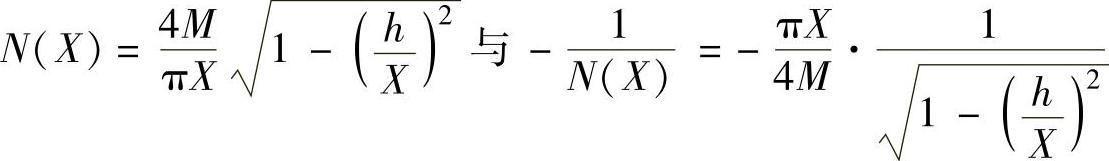

2）线性部分频率特性为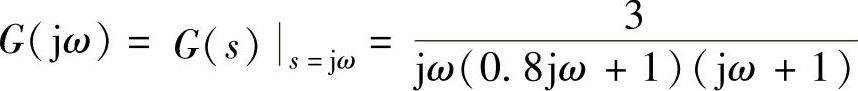，线性部分频率特性曲线与负倒描述函数曲线的交点在反向横轴上，即相频特性为-π。

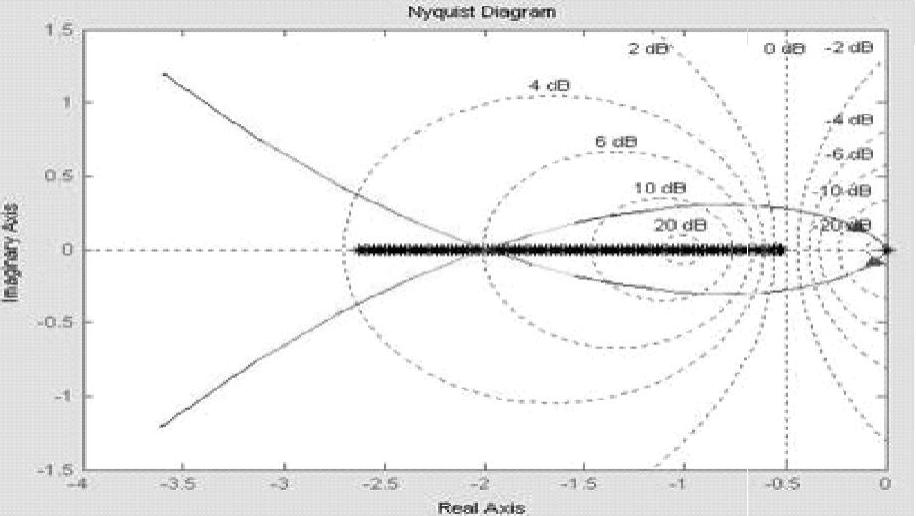
图10-21 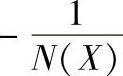与G（jω）曲线

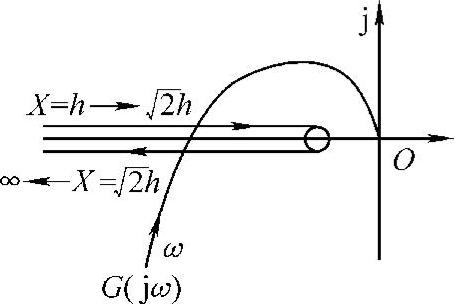
图10-22 图10-21的示意图

①由线性部分的相频特性求ω。

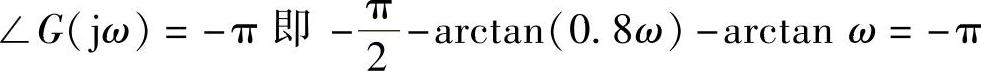
clear；syms omega；

[omega]=solve（-pi/2-atan（0.8∗omega）-atan（1∗omega）=-pi，omega）；

omega=vpa（omega，4），

程序运行后得到线性部分频率特性在反向横轴上交点的角频率为ω=1.118rad/s。

②计算ω对应的|G（jω）|。

clear；w=1.118；G=3/（j∗w∗（0.8∗j∗w+1）∗（1∗j∗w+1））；A=abs（G），

程序运行后得到交点角频率ω=1.118rad/s对应的|G（jω）|=1.3334。

3）为使系统不产生自振，线性部分的频率特性曲线与负倒描述函数曲线应不相交，即

有负倒描述函数的极值<|G（jω）|，那么有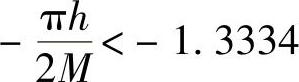，则参数M与h的关系为

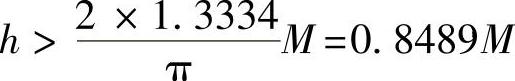
4）当取M=1与h=0.9时，满足h>0.8489M，即G（jω）与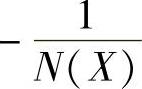曲线应不相交、系统不产生自振。以下使用MATLAB程序来绘制G（jω）与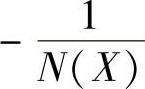曲线。

clear；syms t x y z h M X；

M=1；h=0.9；

for X=0.5：0.1：10

x=4∗h/（pi∗X）∗sqrt（1-（h/X）^2）；

y=0；plot（-1/x，y，k∗），grid on；hold on；

end

n=[0003]；

d=conv（conv（[10]，[0.81]），[11]）；

G=tf（n，d）；

for w=0.7：0.1：8

nyquist（G，[w，w+0.1]），grid on；

hold on；

end

程序运行后，绘制出图10-23，即系统频率特性与负倒描述函数曲线是不相交的。

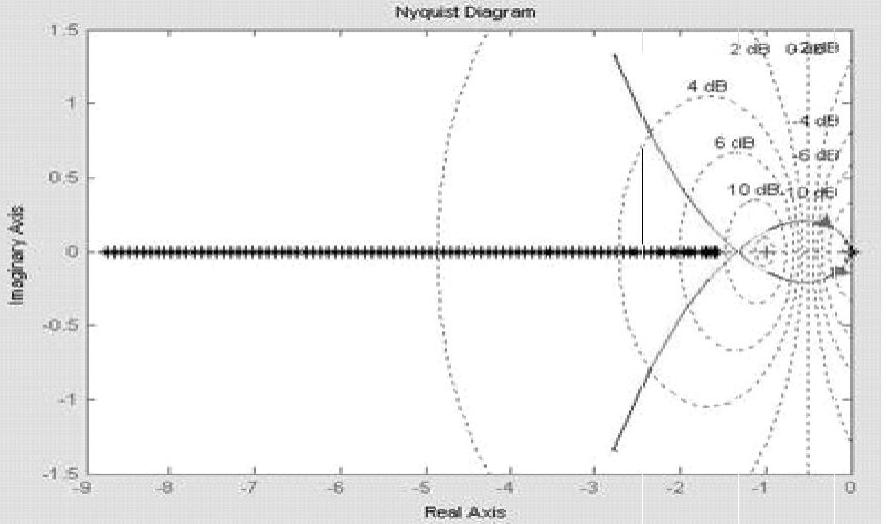
图10-23 频率特性与负倒描述函数曲线不相交

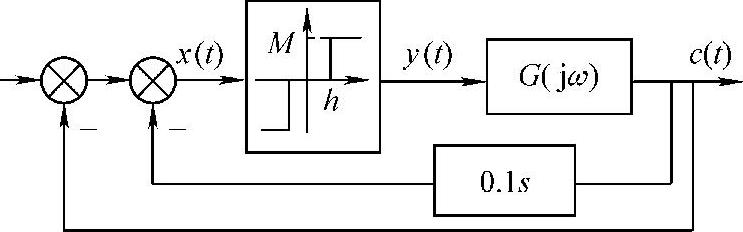
图10-24 带有死区继电特性的系统

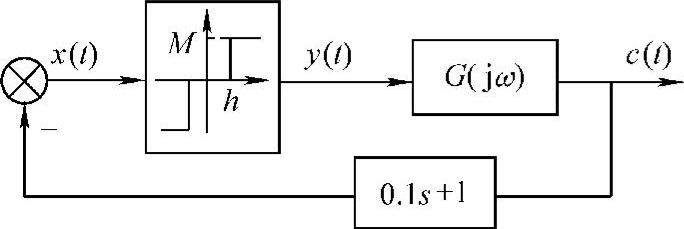
图10-25 系统简化结构

【例10-7】 已知带有死区继电特性的系统结构如图10-24所示，线性部分的传递函数为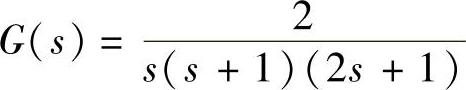，M=1.7、h=0.7。试分析该系统是否存在自振。若有自振，需求出自振的振幅X与角频率ω。

解：1）系统简化后如图10-25所示，即系统线性部分传递函数为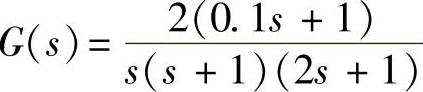，那么线性部分的频率特性为。

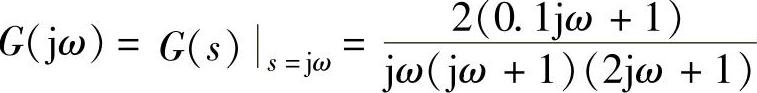2）在同一复平面上绘制非线性特性负倒描述函数与线性部分的Nyquist曲线。

clear；syms t x y z h M X；

M=1.7；h=0.7；

for X=0.8：0.1：6

x=4∗M/（pi∗X）∗sqrt（1-（h/X）^2）；

y=0；plot（-1/x，y，k∗）；grid on；hold on；

end

n=[0.22]；

d=conv（conv（[10]，[11]），[21]）；

G=tf（n，d）；

for w=0.7：0.1：4

nyquist（G，[w，w+0.1]），grid on；hold on；

end

运行该程序得到在同一复平面上绘制的G（jω）与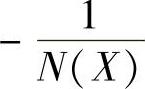的曲线，如图10-26所示。

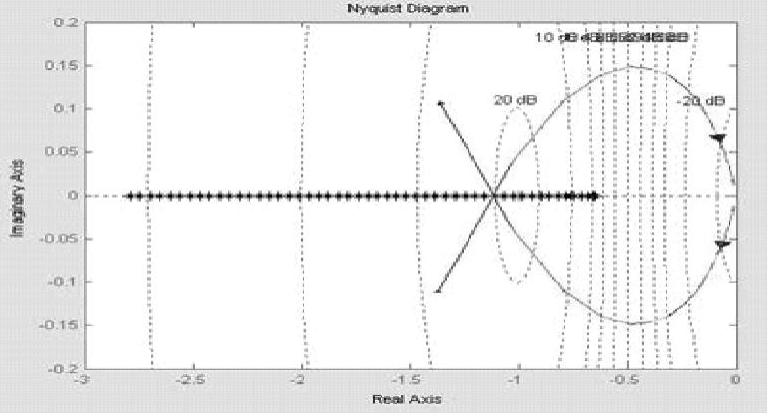
图10-26　G（jω）与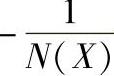曲线

3）因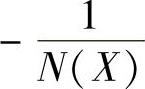是X实函数，与G（jω）画在同一复平面内时，交点必在横坐标上。利用虚部为零，求交点角频率ω与交点的G（jω）。因为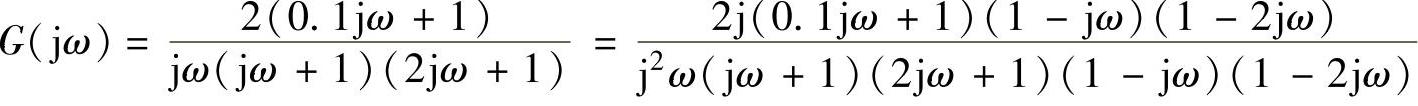

①分母有理化后，运行以下程序段只关注以上分式的分子（是一复数）：

clear；syms w n；n=expand（j∗（1+0.1∗j∗w）∗（1-j∗w）∗（1-2∗j∗w）），

程序段运行后得到n=i+29/10∗w-17/10∗i∗w^2+1/5∗w^3。

②利用交点的虚部为零，求交点的角频率ω。

clear；[w]=solve（1-17/10∗w^2=0）；w=vpa（w，4），

程序段运行后得到交点的角频率ω=0.767rad/s。

③由角频率ω=0.767rad/s，按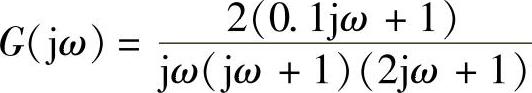计算交点的|G（j0.767）|。

clear；syms w；w=0.767；

G=2∗（0.1∗j∗w+1）/（j∗w∗（1∗j∗w+1）∗（2∗j∗w+1））；A=real（G），

程序段运行后得到|G（j0.767）|=-1.1332。

4）对于负倒描述函数，利用交点在横坐标上，其虚部为零，求自振的振幅X。

①死区继电特性的描述函数N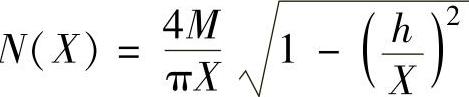，求负倒描述函数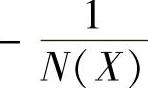的

表达式。

clear；syms X M h f；M=1.7；h=0.7；f=-pi∗X/（4∗M∗sqrt（1-（h/X）^2）），

程序段运行后得到f=-25/17∗pi∗X/（100-49/X^2）^（1/2）。

②利用交点在横坐标上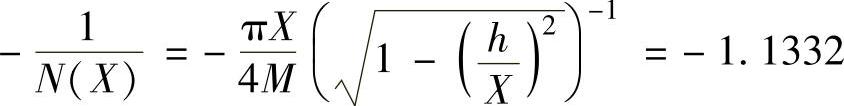，，求自振的振幅X。

clear；syms X；[X]=solve（-25/17∗pi∗X/（100-49/X^2）^（1/2）=-1.1332，X）；X=vpa（X，4），

程序段运行后得到两个振幅X₁=0.7336与X₂=2.341。

5）结论。线性部分的频率特性曲线与相对负描述函数有两个交点，交点的角频率ω=0.767rad/s，自振有两个振幅X₁=0.7336与X₂=2.341。对应着系统两个一次近似下的周期运动状态，类似图10-3中M₂交点的分析，确定X₂=2.341是自振点。

【例10-8】 设带有滞环继电特性的系统结构如图10-27所示，其中非线性特性的参数为M=4、h=1；线性部分的传递函数为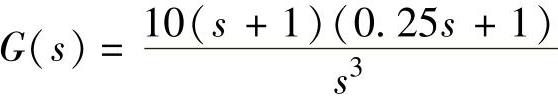。试分析该系统是否存在自振。若有自振，需求自振的振幅X与角频率ω。

解：1）系统线性部分传递函数为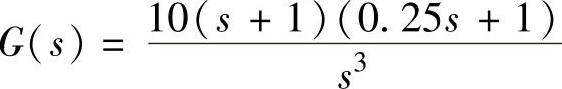，那么线性部分的频率特性为

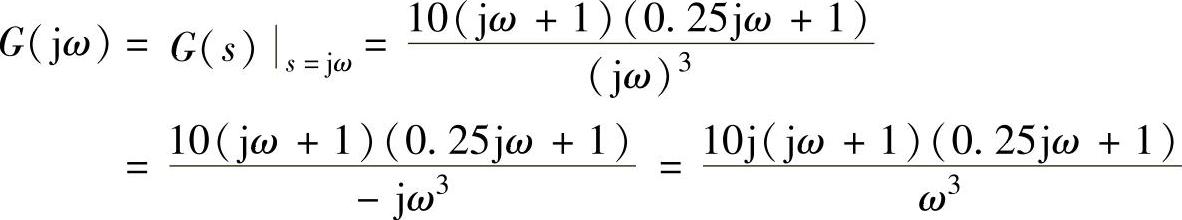
用程序计算线性部分频率特性的实频与虚频。

clear；syms w G；

G=10∗j∗（1+j∗w）∗（1+0.25∗j∗w）/（w^3）；G=expand（G），

程序运行后得到G=10∗i/w^3-25/2/w^2-5/2∗i/w，即实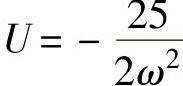频，虚频。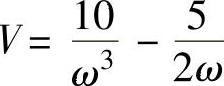

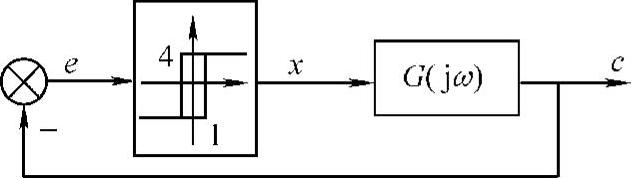
图10-27 带有滞环继电特性的系统

2）系统非线性特性的负倒描述函数。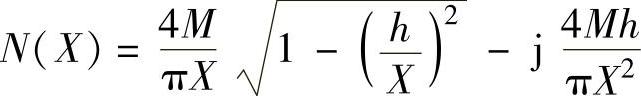，已知M=4，h=1，则有描述函数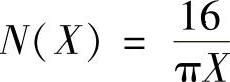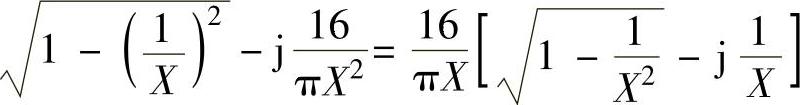，那么对应负倒描述函数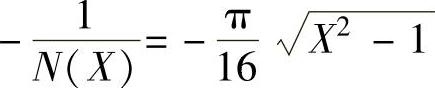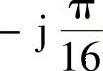，即负倒描述函数的实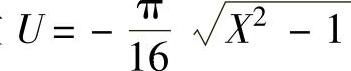频函数，虚频函数。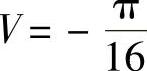

3）如果非线性特性的负倒描述函数与线性部分的Nyquist曲线相交，则可能产生自振，此时两个复变量实部与实部相等，虚部与虚部相等。

①利用虚部相等求ω。

clear；syms w real；

[w]=solve（10/（w^3）-5/（2∗w）=-pi/16，w）；

w=vpa（w，4），

程序运行后得到自振角频率ω=12.4rad/s。

②利用实部相等求X。

利用求出的自振角频率ω=12.4rad/s计算线性部分频率特性的实频。

clear；syms w X U；w=12.4；U=-25/（2∗w^2），

程序运行结果U=-0.0813。

利用求出的线性部分频率特性的实频求X。

clear；syms X；

[X]=solve（-0.0813=-pi/16∗sqrt（X^2-1），X）；X=vpa（X，5），

程序运行后得到自振的振幅X=1.0823。

4）在同一复平面上绘制非线性特性的负倒描述函数与线性部分的Nyquist曲线。

clear；syms w x y X；

for X=0.01：0.1：20

x=-pi/16∗sqrt（X^2-1）；

y=-pi/16；plot（x，y，k∗），hold on；

end

n=conv（conv（[010]，[11]），[0.251]）；d=[1000]；G=tf（n，d）；

for w=1.8：0.1：80

nyquist（G，[w，w+0.1]），grid on；hold on；

end

运行该程序，在同一复平面上绘制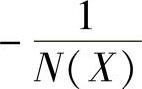与G（jω）曲线，如图10-28所示，其示意图如图10-29所示。

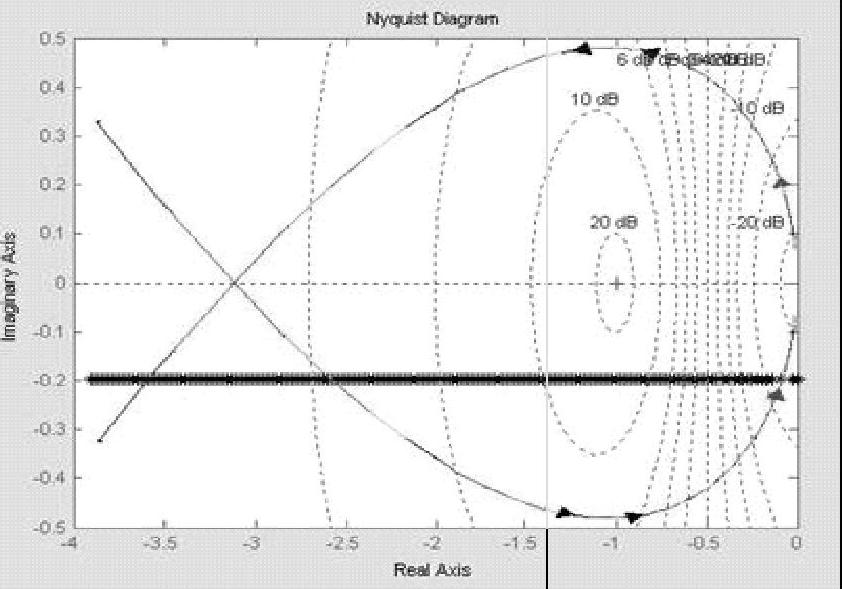
图10-28 系统的G（jω）与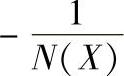曲线

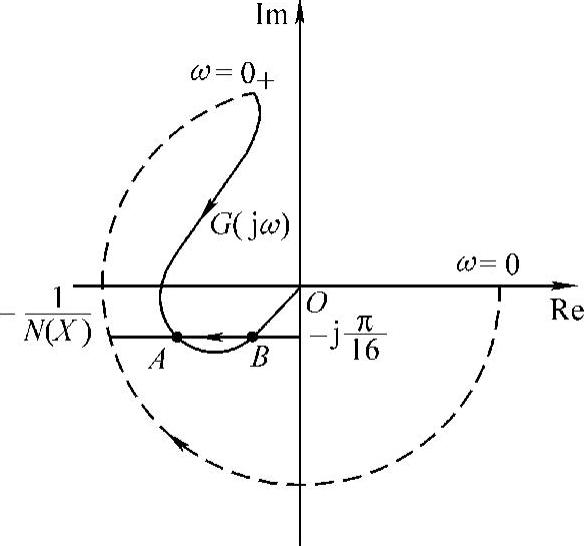
图10-29 图10-28曲线示意图

由图10-29可以看出，系统的G（jω）与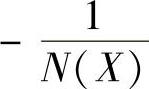曲线有两个交点。要特别注意系统G（jω）表达式与其增补特性，再按图10-3的分析，左侧交点A不是自振点，右侧交点B是自振点，其自振的角频率ω=12.4rad/s，自振的振幅X=1.0823。