了解控制系统Nyquist曲线

频率特性G（jω）是ω的复变函数，在G（jω）复平面上对于某一ω可以用一矢量或其端点（坐标）来表示。当ω从0→∞时，G（jω）端点的极坐标轨迹即是频率特性的极坐标图，叫做幅相特性曲线或Nyquist曲线（图）。

在介绍用Nyquist曲线法判断系统稳定性时，已经介绍了nyquist（）函数的调用格式，并已说明函数命令执行后绘制的Nyquist曲线默认角频率ω范围为（-∞，+∞）。系统在-∞≤ω≤+∞时的完整开环频率响应G（jω）H（jω），其中，范围-∞≤ω≤0的G（-jω）H（-jω）曲线部分与范围0≤ω≤+∞的曲线部分G（jω）H（jω）对称于G（s）H（s）平面的实轴。在自动控制原理的各种教科书中，一般只绘制0≤ω≤+∞时的幅相特性曲线，这仅是MATLAB中的函数命令nyquist（）执行后，绘制的对于横轴对称的幅相特性曲线的关于0≤ω≤+∞范围的部分。在此提醒读者看Nyquist曲线时注意。

【例9-8】 已知单位负反馈系统开环传递函数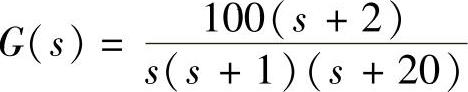，1）用频率特性法判别闭环系统稳定性；2）用Nyquist曲线法再判别闭环稳定性；3）再用阶跃响应验证上述判断。

解：1）绘制Bode图判别闭环系统稳定性。

clear；n=100∗[12]；d=conv（[110]，[120]）；s=tf（n，d）；margin（s），grid；

程序运行后绘制系统开环Bode图，如图9-8所示，并计算出系统性能指标如下。

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=65.4° 剪切频率：ω_c=5.11rad/s

以上指标说明，系统不仅稳定，而且性能非常优良。

2）复习增补开环频率响应。

根据自动控制原理^[9]，当系统开环传递函数含有积分环节时，即s平面原点处有开环极点，为有效应用Nyquist判据，需要对频率响应加以修正，即有所谓增补频率响应。

在绘制Nyquist曲线时，当系统开环传递函数含有ν个积分环节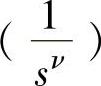时，在ω=0处给特性曲线补充一个半径为无穷大、负转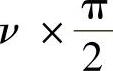的大圆弧，随后再随ω的增加绘制原特性曲线。这样绘制的曲线就叫做增补Nyquist曲线。

3）绘制Nyquist曲线判别闭环系统稳定性。

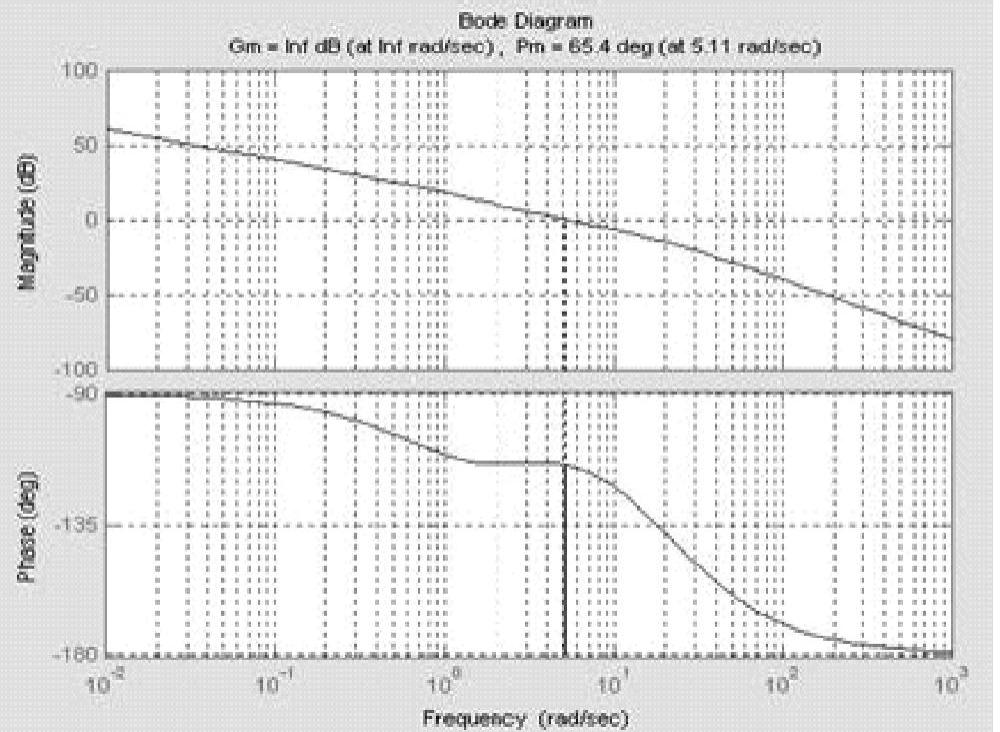
图9-8　　系统开环Bode图

clear；n=100∗[12]；d=conv（[110]，[120]）；s=tf（n，d）；nyquist（s），

程序运行后绘制Nyquist曲线，如图9-9所示。经增补后可知，关键点（-1、j0）在Nyquist曲线外。根据自动控制原理，系统开环特征方程零根视为稳定根，本题开环不稳定根的个数p=0，而Nyquist曲线完全不包围（-1、j0）点，或Nyquist曲线按逆时针方向包围（-1、j0）点的次数p=0，根据Nyquist稳定判据，闭环系统稳定，与Bode图法判定结果相同。

4）用阶跃响应曲线验证上述判断。

clear；n=100∗[12]；d=conv（[110]，[120]）；

s=tf（n，d）；sys=feedback（s，1）；step（sys），grid；

程序运行后绘制阶跃响应曲线，如图9-10所示。曲线图显示，闭环系统不仅稳定，而且时域性能非常优良，均说明上述两法判断正确。

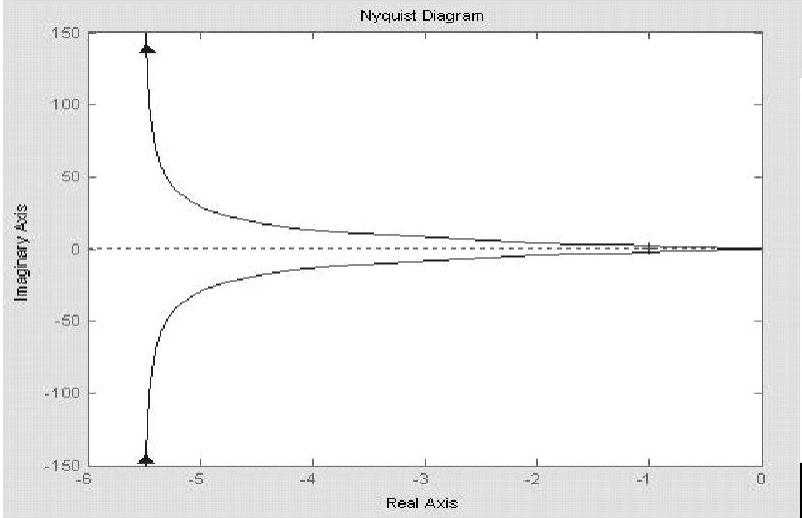
图9-9　　系统Nyquist曲线

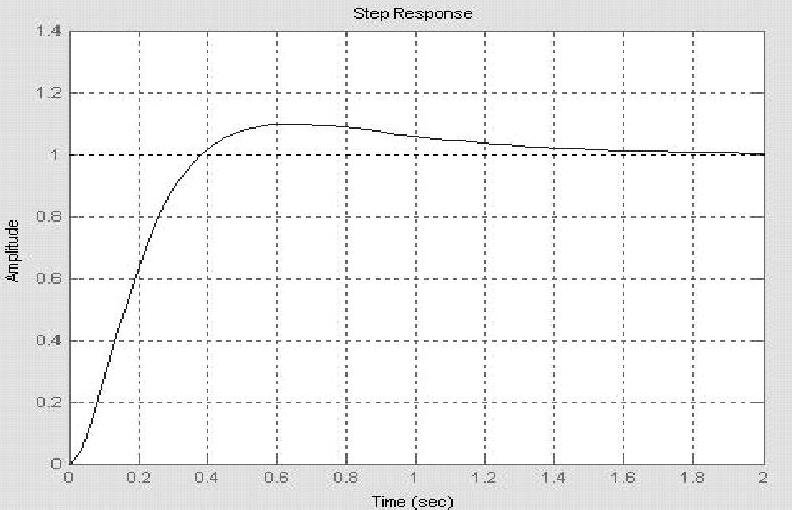
图9-10　　单位阶跃响应曲线

【例9-9】　　已知单位负反馈系统前向通道传递函数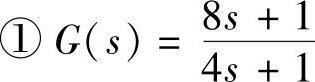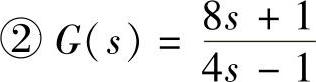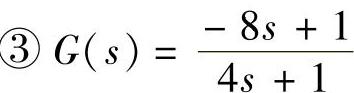：、、。1）试绘制G（s）的Nyquist曲线并对系统闭环判稳；2）试分别绘制系统闭环的阶跃响应曲线并验证以上判稳结论。

解：1）绘制三个系统G（s）的Nyquist曲线并对系统闭环判稳。

clear；n1=[81]；d1=[41]；G1=tf（n1，d1）；nyquist（G1），grid；hold on；

n2=[81]；d2=[4-1]；G2=tf（n2，d2）；nyquist（G2），grid；hold on；

n3=[-81]；d3=[41]；G3=tf（n3，d3）；nyquist（G3），grid；

程序运行后绘制三个系统G（s）的Nyquist曲线，如图9-11所示。系统1的p=0，其Nyquist曲线为图中的右边小圆，远离（-1、j0）点，故系统闭环稳定。系统2的Nyquist曲线为图中的中部大圆，其Nyquist曲线虽不包围（-1、j0）点，但p=1，故系统闭环不稳定。系统3的Nyquist曲线为图中的左边大圆，其Nyquist曲线顺时针包围（-1、j0）点，但p=1，故系统闭环不稳定。(www.xing528.com)

2）绘制系统闭环的阶跃响应曲线并验证以上判稳结论。

①系统1。

clear；n1=[81]；d1=[41]；G1=tf（n1，d1）；sys1=feedback（G1，1）；step（sys1），grid；

程序运行后绘制系统闭环阶跃响应曲线，如图9-12所示。曲线显示系统闭环稳定，与以上判稳结论一致。

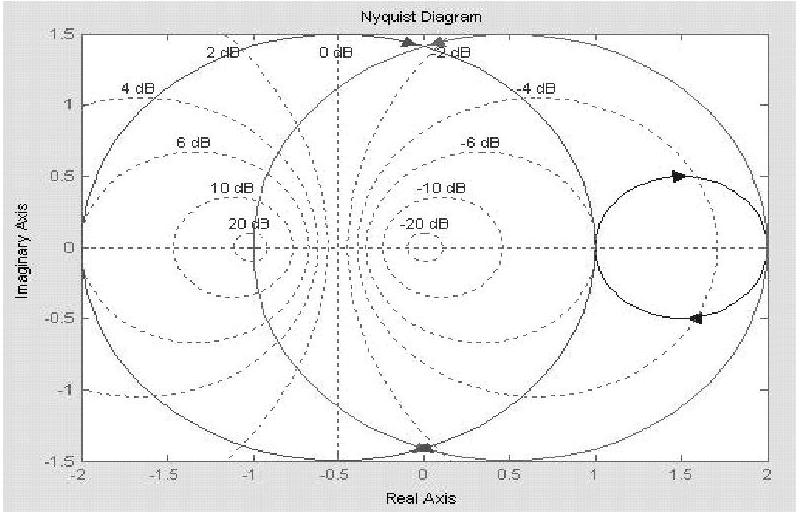
图9-11　三个系统G（s）的Nyquist曲线

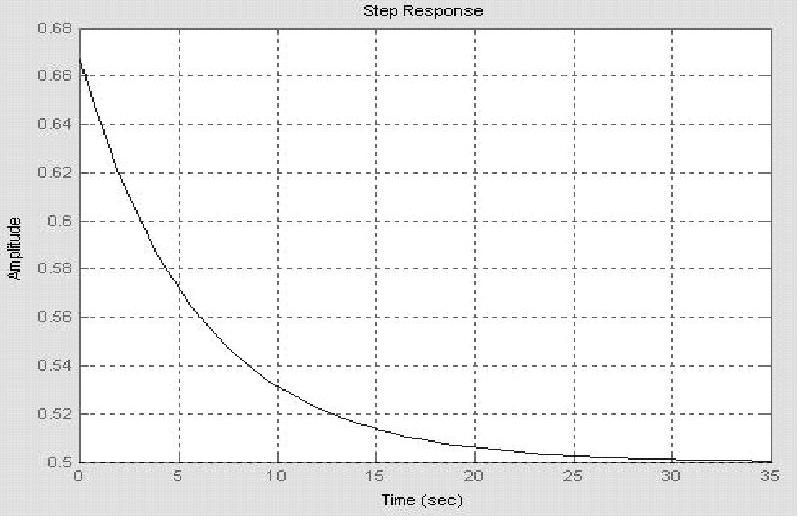
图9-12　闭环系统1阶跃响应曲线

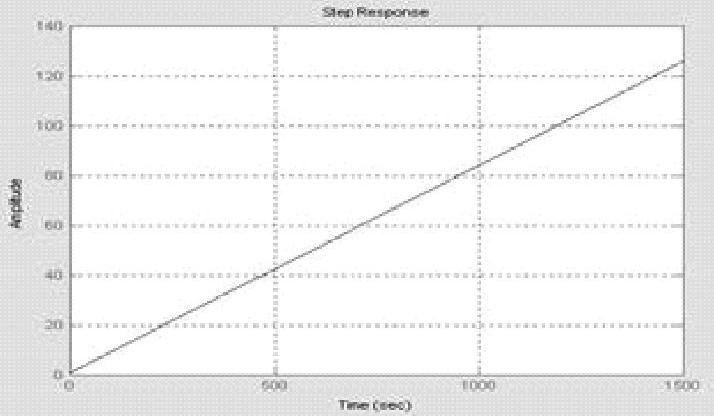
图9-13　插图闭环系统2阶跃响应曲线

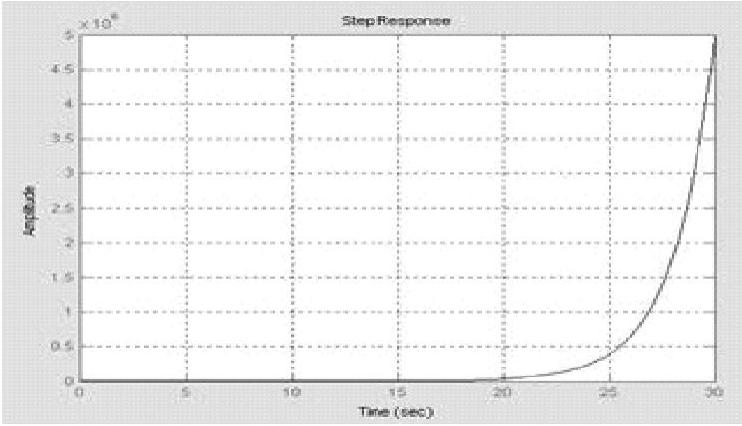
图9-14　闭环系统3阶跃响应曲线

②系统2。同系统1，绘制系统闭环阶跃响应曲线，如图9-13所示。曲线显示系统正向发散，闭环不稳定，与以上判稳结论一致。

③系统3。同系统1，绘制系统闭环阶跃响应曲线，如图9-14所示。曲线显示系统正向发散，闭环不稳定，与以上判稳结论一致。

【例9-10】 某具有延迟环节的非最小相位系统的开环传递函数为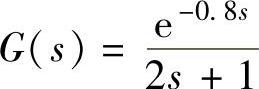。1）试绘制系统Nyquist曲线并判别系统稳定性。2）绘制系统阶跃响应曲线验证以上判别。

解：1）复习最小相位与非最小相位环节（或系统）。

传递函数中有右极点、右零点的环节（或系统）叫做非最小相位环节（或系统）；而传递函数中没有右极点、右零点的环节（或系统）叫做最小相位环节（或系统）。例如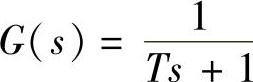，即惯性环节是最小相位环节、一阶不稳定环节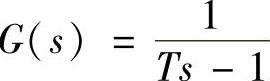是非最小相位环节等。

2）绘制系统Nyquist曲线。

clear；n1=[1]；d1=[21]；G1=tf（n1，d1）；tau=0.8；

[np，dp]=pade（tau，2）；Gp=tf（np，dp）；G=G1∗Gp；nyquist（G），

程序运行后，绘制系统的Nyquist曲线，如图9-15所示。由于该系统的滞后相移随ω→∞而无限增大，以及幅频特性衰减到零，其Nyquist曲线在趋向坐标原点的过程中，将多次包围坐标原点。关键点（-1、j0）在Nyquist曲线外。根据自动控制原理，本题开环不稳定极点个数p=0，而Nyquist曲线完全不包围（-1、j0）点，根据Nyquist稳定判据，闭环系统稳定。

3）绘制系统闭环阶跃响应曲线。

clear；n1=[1]；d1=[21]；G1=tf（n1，d1）；tau=0.8；[np，dp]=pade（tau，2）；

Gp=tf（np，dp）；G=G1∗Gp；sys=feedback（G，1）；step（sys），grid；

程序运行后，绘制系统闭环阶跃响应曲线，如图9-16所示。由图可知，系统闭环稳定，与Nyquist稳定判据判断结论一致，而且系统时域性能优良。

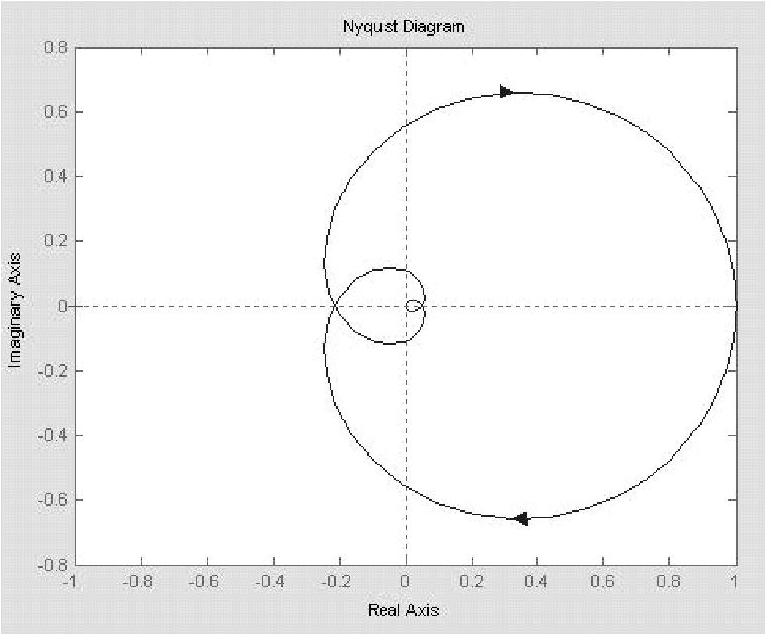
图9-15 系统的Nyquist曲线

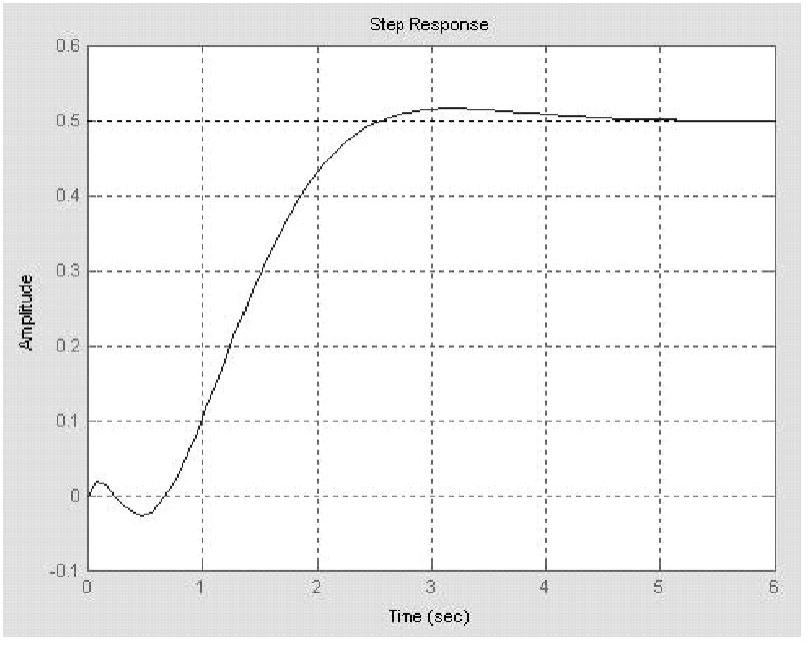
图9-16 系统闭环阶跃响应曲线